Первые интегралы дифференциальных систем и основные теоремы о них.
Рассм. с-му:  (1), т.е.
(1), т.е.  где
где 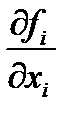 непрер. в области D.
непрер. в области D.
ОПР.Дифференцируемая ф-я 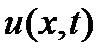 наз. первым интегралом с-мы (1), если она отлична от постоянной, но любое решение
наз. первым интегралом с-мы (1), если она отлична от постоянной, но любое решение 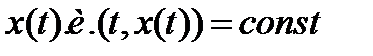
Если t интегрировано как время, а xкак в-р пр-ва некот. реальной системы, то тождество 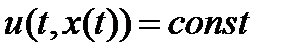 означает, что величина uc течением времени не меняется. Поэтому если
означает, что величина uc течением времени не меняется. Поэтому если 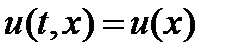 не зависит явно от t, то это и является законом сохранения.
не зависит явно от t, то это и является законом сохранения.
Т. Дифференцируемая функция 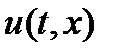 отличная от постоянной, явл. первым интегралом системы (1) т. и т.т, когда
отличная от постоянной, явл. первым интегралом системы (1) т. и т.т, когда 
Д-ВО: неох. дано: 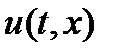 -1-й интеграл. док-ть:
-1-й интеграл. док-ть: 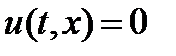 . достаточно доказать: для любого
. достаточно доказать: для любого 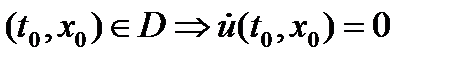
Пусть  -произв точка по области D. ч/з эту точку проходит решение
-произв точка по области D. ч/з эту точку проходит решение 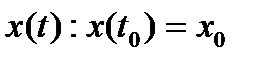 . Для этого решения
. Для этого решения 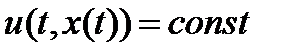 . Продиф. это тождество, получим
. Продиф. это тождество, получим 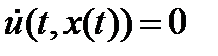 . Пусть
. Пусть 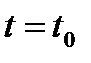 получим
получим 
достаточность: дано:  док-ть:
док-ть: 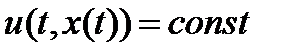 . В нашем случае
. В нашем случае  , это значит
, это значит
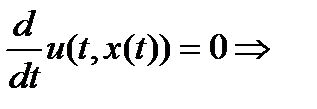
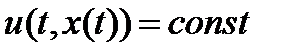 .чтдРассм.
.чтдРассм.  (1). Пусть
(1). Пусть  -1-й интеграл в этой системе
-1-й интеграл в этой системе
Т. Если известен 1-й интеграл 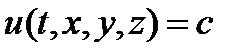 с-мы (1), то размерность (порядок) этой системы можно понизить на 1.{т.е. зная 1-й интеграл с-му (1) состоящую из 3-х ур-ий свести к системе сост. из 2-х ур-ий}
с-мы (1), то размерность (порядок) этой системы можно понизить на 1.{т.е. зная 1-й интеграл с-му (1) состоящую из 3-х ур-ий свести к системе сост. из 2-х ур-ий}
6. Найти 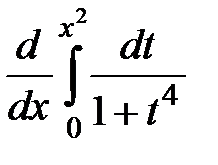 .
.
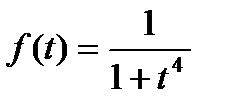 непрерывная на [0; x2]
непрерывная на [0; x2]
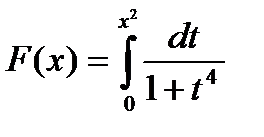
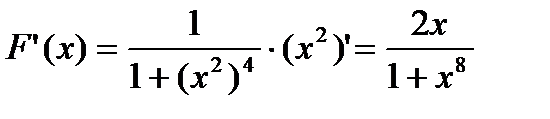 .
.
Ответ: 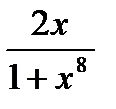 .
.
6. Какие из следующих множеств попарно гомеоморфны:
(- 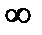 ;3]; [1;5) ; (-7; 2) и [2, 3]. Рассматривается естественная топология.
;3]; [1;5) ; (-7; 2) и [2, 3]. Рассматривается естественная топология.
Решение:f-гомеоморфизм, если f-биекция, f-непрерывно, f-1 –непрерывно. Т.к. при непрерывном отображении открытые®откр, замкнутые®замкн., то след. рассматривать мн-ва (- 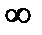 ;3]=А и[1;5)=В. Найдем отображение f:А®В Þf=-
;3]=А и[1;5)=В. Найдем отображение f:А®В Þf=- 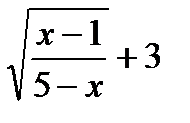 , по теореме об обратном отображении f(x)-инъективно, сюръективно, а биективно. То по определению f- гомеоморфно.
, по теореме об обратном отображении f(x)-инъективно, сюръективно, а биективно. То по определению f- гомеоморфно.
|
|
|
Билет 7
ИнтегралРимана(определение,существование,свойства;диф-мость интеграла Римана по верхнему пределу). Сущ-вание первообразной у непр-вной ф-ции. Формула Ньютона-Лейбница.
Опр. Пусть f(x) функция заданная на [a;b]; 1. Разбиением отрезка [a;b] называется система точек x0, x1,...,xn: такая что a= x0<x1<x2<…<xn=b; 2. Разбиением с отмеченными точками называется разбиение и система точек 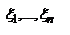 такие что
такие что 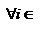 [xi-1;xi]; 3. Диаметром разбиения называется
[xi-1;xi]; 3. Диаметром разбиения называется 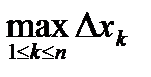 . Обозначения (P;
. Обозначения (P; 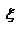 ) - разбиение с отмеченными точками;
) - разбиение с отмеченными точками; 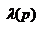 - диаметр разбиения; P - разбиение.
- диаметр разбиения; P - разбиение.
Опр. Интегральной суммой функции f для данного разбиения (P; 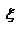 ) называется сумма
) называется сумма 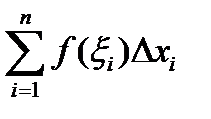 и обозначается
и обозначается 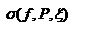 .
.
Опр. Число I называется определённым интегралом ф-ции f на [a;b], если  >0
>0  >0:
>0:  с диаметром
с диаметром 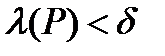
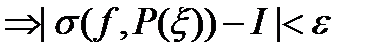 .
.
Опр. Интегралом функции f на [a;b] называют предел интегральных сумм при 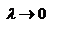 и обозначается
и обозначается 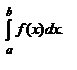 =
= 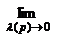
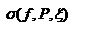 .
.
Функция называется интегрируемой по Риману, если у нее  интеграл.
интеграл.
Необходимое условие интегрируемости: Если функция интегрируема на отрезке [a;b], то она ограничена на нем.
Необходимое и достаточное условие интегрируемости (критерий Дарбу интегрируемости по Риману): Для того чтобы ф-ция f была интегрируема на [a;b]  чтобы она была огр и удовлетв условию
чтобы она была огр и удовлетв условию  >0
>0  >0:
>0: 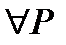 с
с 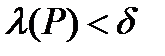 , имеем:
, имеем: 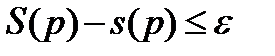 .
.
|
|
|
R[a;b] – класс всех функций интегрируемых по Риману на [a;b]. 
Т(св-во линейности). 1. 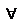 f ,g
f ,g  R[a;b], f+g
R[a;b], f+g  R[a;b]; 2.
R[a;b]; 2.  f
f 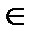 R[a;b] ,
R[a;b] , 

 R,
R, 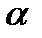 f
f 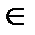 R[a;b] ; 3.
R[a;b] ; 3.  f,g
f,g 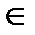 [a;b]
[a;b] 
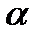 ,
, 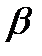
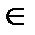 R
R 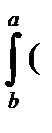
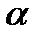 f+
f+ 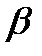 g)dx=
g)dx= 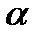
 +
+ 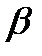
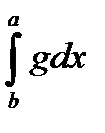 .
.
Т(св-во интегрируемости произведения)Пусть f ,g  R[a;b]
R[a;b] 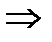 f*g
f*g  R[a;b]
R[a;b]
Т(св-во)Пусть a<c<b, если f  R[a;c] и f
R[a;c] и f  R[c;b], тогда ф-ция f
R[c;b], тогда ф-ция f  R[a;b] и
R[a;b] и 
Т(неотриц интегралов)Пусть f  R[a;b] и
R[a;b] и  на [a,b], тогда
на [a,b], тогда 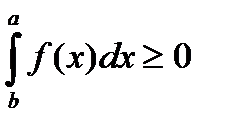
Т(св-во интегр-ти модуля)Если ф-ция f  R[a;b]
R[a;b] 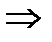
 и
и 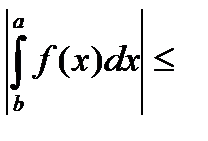
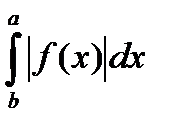
Дифференцируемость интеграла Римана по верхнему пределу.
Опр. Пусть f  R[a;b], тогда f
R[a;b], тогда f  R[a;х] ,
R[a;х] ,  [a;b] определён
[a;b] определён 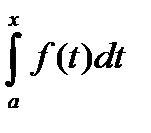 и ф-ция F:
и ф-ция F:  [a;b]
[a;b] 
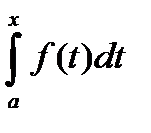 эту функцию наз опред интеграл с переменным верхним пределом и обозн F(x)=
эту функцию наз опред интеграл с переменным верхним пределом и обозн F(x)= 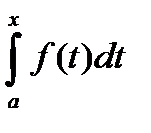 .
.
Т (диф-ть интеграла с переменным верхним пределом): Пусть f  R[a;b], и f непрерывна в точке x0
R[a;b], и f непрерывна в точке x0 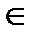 [a;b], тогда F(х) диф-ма в x0, и
[a;b], тогда F(х) диф-ма в x0, и 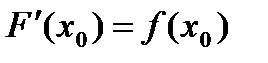 .
.
Доказательство. Рассмотрим  [a;b], F(x0+
[a;b], F(x0+  x)-F(x0)=
x)-F(x0)= 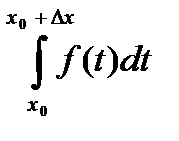 =
= 
 x, где inff(x0)
x, где inff(x0) 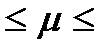 supf(x0),
supf(x0),  , рассмотрим
, рассмотрим 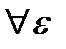 >0 учитывая непрерывность f(x0)
>0 учитывая непрерывность f(x0) 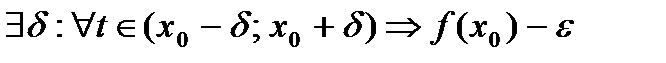 <f(t)<
<f(t)< 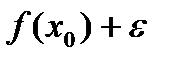
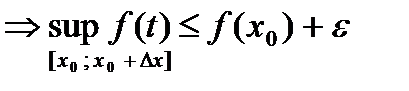 ,
, 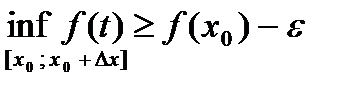 , если
, если 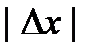 <
< 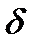 , и
, и 
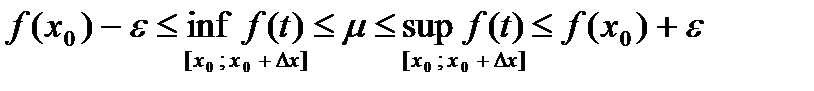
 , тоесть
, тоесть  <
<  .
.
Т(непр интеграла с пер верх пределом) Если f  R[a;b],то F(x)
R[a;b],то F(x)  С[a;b]
С[a;b]
Опр. Функция F(x) называется первообразной функции f(x) на [a;b]. Если заданы ф-ции f(x) и F(x) (F(x) непрерывна на [a;b]) и 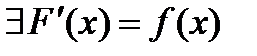 ,
, 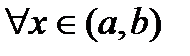 .
.
Т(О существовании первообразной): Пусть f  С[a;b], тогда для этой ф-ции на [a,b]
С[a;b], тогда для этой ф-ции на [a,b]  первообразная F(x)=
первообразная F(x)= 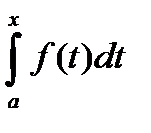 и причём
и причём 
Д-во. Возьмём произвол. т. 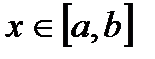 f непр в т.х. По пред. Теореме имеем
f непр в т.х. По пред. Теореме имеем  , т.е. ф-ция F явл. первообр. для f.
, т.е. ф-ция F явл. первообр. для f.
|
|
|
Т(Формула Ньютона-Лейбница): Пусть f  С[a;b], и Ф(х) какая либо первообр ф-ции f , тогда справед формула Ньютона-Лейбница
С[a;b], и Ф(х) какая либо первообр ф-ции f , тогда справед формула Ньютона-Лейбница 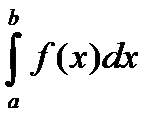 =
= 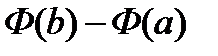
Доказательство. Т.к. f(x) – непрерывна всюду кроме конечного числа точек и ограничена, то она интегрируема. Пусть 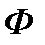 (x) – одна из обобщенных первообразных, обозначим через F(x)=
(x) – одна из обобщенных первообразных, обозначим через F(x)= 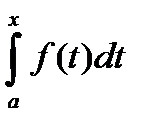 , тогда
, тогда 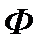 (x)-F(x)
(x)-F(x)  c, тогда
c, тогда 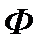 (a)-F(a)=c,
(a)-F(a)=c, 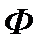 (a)=c;
(a)=c; 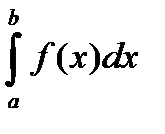 =F(b),
=F(b), 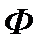 (b)-F(b)=c;
(b)-F(b)=c; 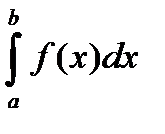 =
= 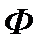 (b)-c=
(b)-c= 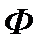 (b)-
(b)- 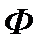 (a). Краткая запись
(a). Краткая запись 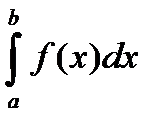 =
= 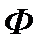 (x)
(x) 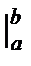 . Формула Ньютона-Лейбница верна, когда a
. Формула Ньютона-Лейбница верна, когда a 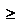 b,
b,  = -
= -  =-(
=-( 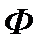 (a)-
(a)- 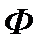 (b))=
(b))= 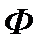 (b)-
(b)- 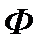 (a).
(a).
Дата добавления: 2018-02-15; просмотров: 676; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
