В партии из 10 деталей содержится 3 нестандартных. На удачу отобраны 2 детали. Найти математическое ожидание и дисперсию числа нестандартных деталей среди отобранных.
Решение: x- число нестандартных решений среди стандартных.
| x | 0 | 1 | 2 |
| P | 7/15 | 7/15 | 1/15 |
P{x=0}=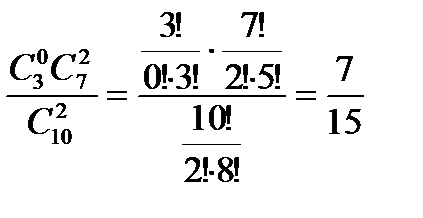 
; P{x=1}= 
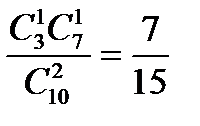; P{x=2}=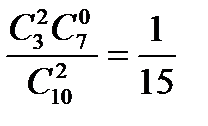 
Mx=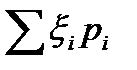 
; Dx= Mx2-( Mx)2
Mx=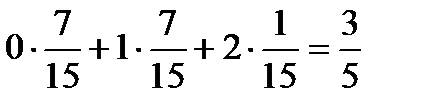 
; Dx= 
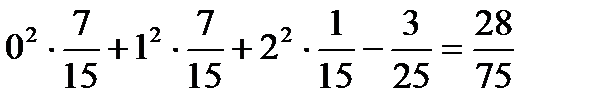
Ответ:Mx=3/5; Dx=28/75.
4. Разложить пространство R4 на прямую сумму подпространств размерности 2.
Решение:R4 – множество строк длины 4 (4-х мерное арифметическое пространство)
R4={(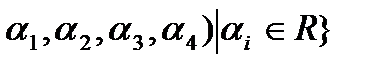 
Если А и В – подпространства пространства V, то через А+В обозначают множество {a+b|aЄA, bЄB}
В случае, если А∩В={Ø} – нулевое подпространство, то такая сумма V=A+B называется прямой и в этом случае пишут V=A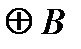 
. В нашем случае Ø=(0,0,0,0)
Пусть теперь А={(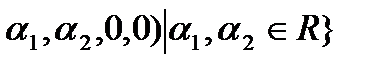 
B={(0,0,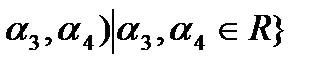 
Проверим, что пространство задаётся в виде А+В
Пусть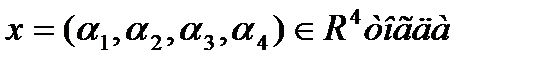 
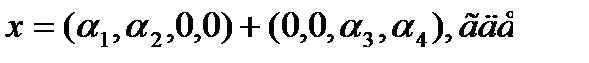а=(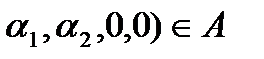 
в==(0,0, 
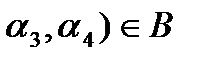, значит R4 =A .
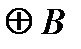Ответ: R4 =A 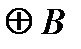, где А={( 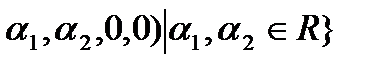B={(0,0,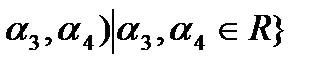
Билет 5
Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа и Коши. Формула Тейлора.
Т(Ферма). Пусть f определена в некоторой окрестности U(x0) и принимает в x0 наибольшее или наименьшее значение по сравнению со значением f в окрест-ности U(x0), тогда если 
в x0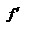 
(x0) хотябы в широком смысле, то она равна нулю.
Доказательство.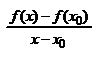 
, 
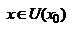. Пусть например x0 наибольшее значение, тогда (*) 
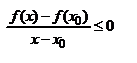при x>x0, x 
U(x0); 
(**) 
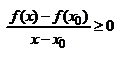при x<x0, x U(x0), тогда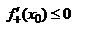 
, 
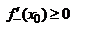т. к. 
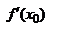
, то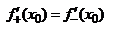 
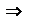они равны нулю и 
.
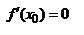Т(Ролля). 1. f непрерывна на [a;b]; 2. Диф-ма на (a;b); 3. f(a)=f(b), тогда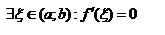 
.
Доказательство. Т. к. f(x) непрерывна на [a;b], то она ограничена и достигает на нем своего наибольшего и наименьшего значения. Если и наибольшее и наименьшее принимаются в концах: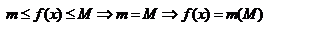 
, тогда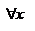 
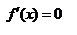. Пусть одно из наибольшего или наименьшего во внутренней точке отрезка, применяем теорему Ферма 
.
|
|
|
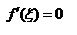Т(Лагранжа). 1. f непрерывная на отрезке [a;b]; 2. Диф-ма на (a;b);, тогда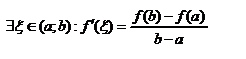 
.Док-во. Рассмотрим функцию F(x)=f(x)- 
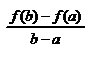(x-a); 1. F(x) непрерывна на [a;b]; 2. производная. F(a)=f(a), F(b)=f(a) применим теорему Ролля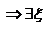 
, 
.
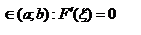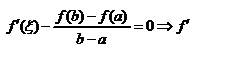
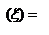
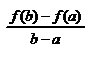Т(Коши). Пусть 1. Функции f и g непрерывны на [a;b]; 2. Дифференцируемы на (a;b); 3.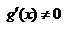 
на (a;b), тогда 
.
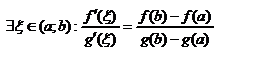Док-во. Докажем, что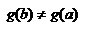 
от противного. Предположим g(b)=g(a), тогда теорема Ролля применима к функции g, получили противоречие с условием 3. Рассмотрим вспомогательную функцию F(x)=f(x)- 
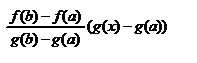. Для F(x) выполнимы условия теоремы Ролля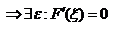 
.
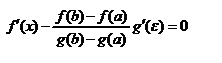Формула Тейлора. Пусть f диф-ма в точке x0,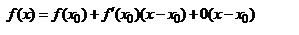 
, 
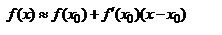. Если f(x) имеет производную1-го порядка, то f представима в виде многочлена первой степени +0(x-x0)1.
Опр. Пусть f имеет производную до n-го порядка включительно в точке x0. Многочленом Тейлора функции f в точке x0 наз мн-н
Pn(x)=f(x0)+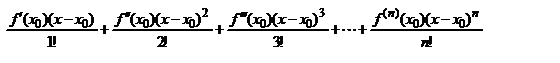 
, Pn(x)= 
. 
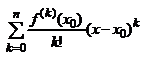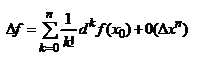- формула Тейлора в дифференциалах.
Решение линейных диф-ных ур-ний с пост-ными коэф-тами Решение линейных систем с постоянными коэффициентами.
Рассм. линейное однородное д.у. с пост коэффиц.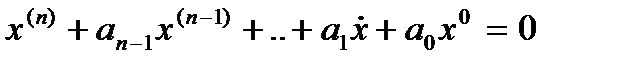 
(1), в кот. 
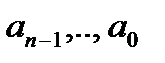- числа. Общее решение этого ур-ия им. вид: 
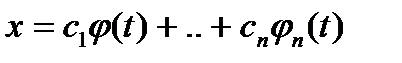, где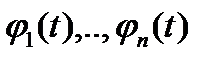 
- фундаментальная с-ма решений.
Для простоты будем рассм. линейное однородное д.у. второго порядка с пост коэффиц.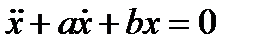 
(1) а,в – числа. 
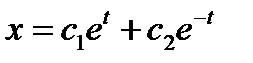- общее решение. Ищем решение в виде 
; 
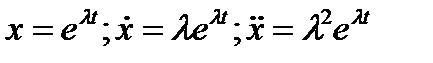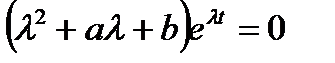
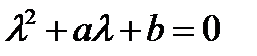- характеристич. ур-ие.
|
|
|
1. 
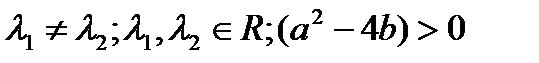, тогда 2 решения: 
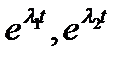. Общее решение: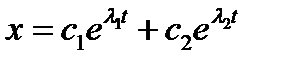 
2. 
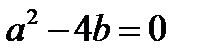, тогда 
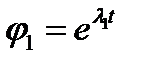. В этом сл. ок-ся, что 
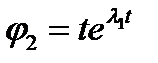- решение.
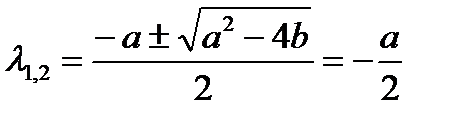значит 
, 
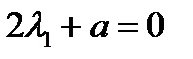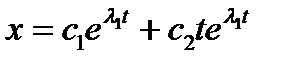
3. 
, 
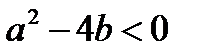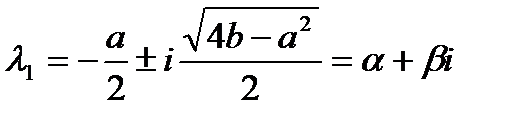, где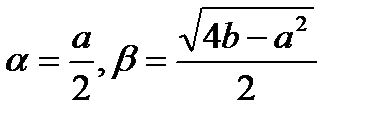 
. В этом сл. решение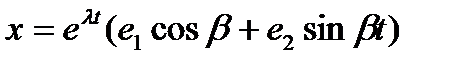 
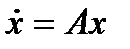, где А-постоян 
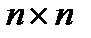матр. Методом исключ эта сист свод к лин однор Ур-ю с пост коэф. Рассм случаи: 1) Пусть ур-е 
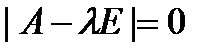им только действит и попарно разл корни 
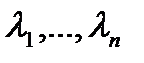. Матр 
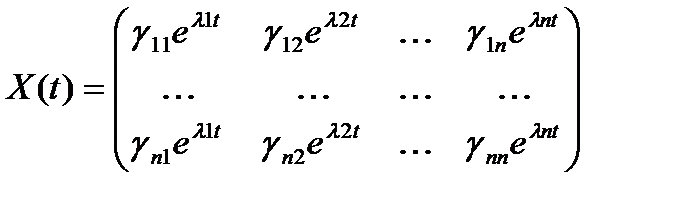явл-ся фундам и поэтому общ реш x=X(t)C. 2) Пусть хар-ое Ур-е им кратные корни, тогда мы не всегда смож постр фундам матр, тогда общ реш 
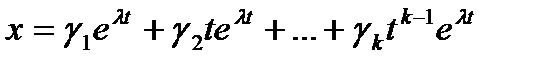; 3) Пусть хар Ур-е им компл корень 
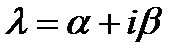кратный к, тогда 
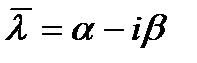тоже будет кр к., тогда реш явл x=u+iv, где u и v – целые. Справ лемма: Пусть x=u(t)+iv(t)- компл знач реш сист 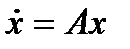, тогда u(t),v(t) –также реш сист 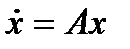, но уже действит. Учитывая эту лемму, общ реш можно стр след обр: 1) постр комплексное знач слаг; 2) выделить в этом постр-и слаг действит и компл части; 3) запис то слаг действит общ реш, кот соотв этим 2-м корням.
5. Докажите, что в пространстве M(2, R) система векторов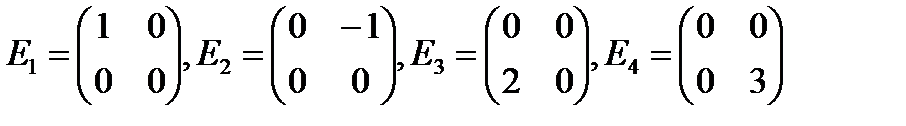 
линейно независима.
Решение: Система векторов а1,а2,а3,а4 линейно независима, если в любой системе вида
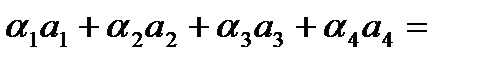Ø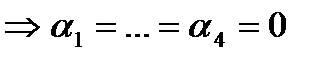 
В нашем случае, пусть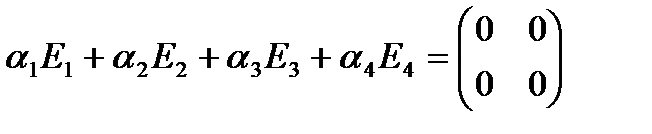 
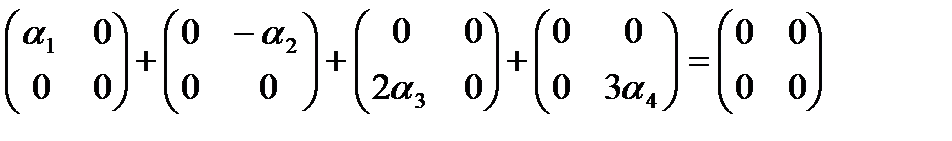
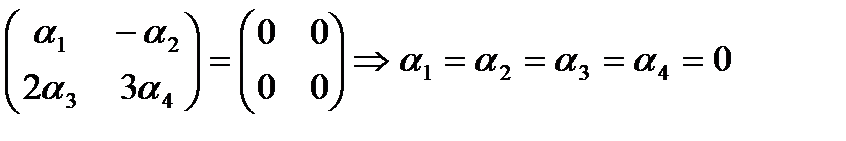
Значит, система векторов Е1, Е2, Е3, Е4 линейно независима.
5Пусть X есть R, а τ состоит из:а) пустого множества и всевозможных бесконечных множеств;
Дата добавления: 2018-02-15; просмотров: 9790; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!