Z-преобразование последовательностей

3.1.4.1. Общие сведения

В теории непрерывных систем существуют три способа их описания, основанные на различных формах представления сигналов:

1) во временной области на основе непосредственного описания сигналов как функции времени;

2) в частотной области на базе спектрального представления сигналов, выполняемого на основе преобразований Фурье;

3) в области функций комплексной переменной с использованием операторного метода представления сигналов на основе преобразования Лапласа.

В теории дискретных систем также используются три перечисленных способа описания систем. При этом третий способ чаще всего реализуется на основе z-преобразования. Возможны его реализации на основе дискретного преобразования Лапласа, однако оно менее удобно и поэтому получило меньшее распространение. Использование z-преобразования позволяет упростить выполнение ряда операций с последовательностями.

Пусть имеется последовательность {x(k×Dt)} -¥<k<¥. Z-преобразование этой последовательности определяется следующим образом:

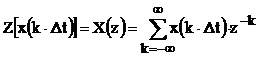(3.29)

где Z[...] – оператор z-преобразования. В качестве z используется некоторая комплексная переменная . Каждому значению z может быть поставлена в соответствие точка в комплексной плоскости. Комплексная функция X(z) определена лишь для тех значений z, для которых степенной ряд (3.29) сходится, т.е. стремится к некоторой конечной величине при k®¥. Совокупность таких значений z называется областью сходимости z-преобразования. Расположение областей сходимости зависит от вида последовательности {x(k×Dt)}. В частности для последовательности конечной длины, ряд (3.29) сходится для всех точек плоскости, за исключением точки z=0. Наряду с обычным z-преобразованием последовательности, определяемым соотношением (3.29), существует понятие одностороннего z-преобразования:

(3.30)

Здесь значение x(kDt) для k<0 не учитывается. Для физически реализуемых последовательностей одностороннее z-преобразование совпадает с обычным. Вычисление z-преобразования конкретных последовательностей можно производить непосредственно по формулам (3.29) и (3.30). Полученные таким образом z-преобразование наиболее часто встречающихся элементарных последовательностей представлены в таблице.

Таблица. Z-преобразование элементарных последовательностей

Вид последовательности	Z-преобразование
	1

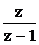
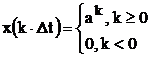
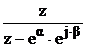
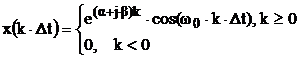
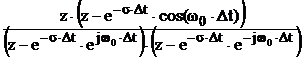
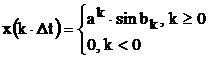
3.1.4.2. Особые точки z-преобразования

В общем случае z-преобразование последовательностей x(k×Dt) может быть описано в виде дробно-рациональной функции , где A(z) и B(z) - полиномы вида:

Корни уравнения A(z)=0 называются нулями z-преобразования, а корни уравнения B(z)=0 называются полюсами. Полюсы и нули являются особыми точками z-преобразования. Они могут быть однократными (простыми) и многократными (сложными).

Например, функция 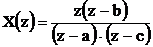имеет два простых (однократных) нуля в точках z₁=0, z₂=b, и два простых полюса р₁=а, р₂=с.

Функция вида 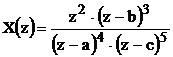в точке z₁=0 имеет 2-х кратный ноль, в точке z₂=b имеет 3-х кратный ноль, в р₁=а имеет 4-х кратный полюс, в р₂=c имеет 5-ти кратный полюс.

Зная расположение полюсов и нулей функции X(z), ее можно восстановить с точностью до константы, записав:

Если в последнем выражении перемножить сомножители и привести подобные члены, то придем к наиболее общей форме записи X(z) в виде дробно-рационалной функции от z^-1:

Каждой последовательности x(kDt) характерно свое расположение и свой тип особых точек в z-плоскости. В частности, зная расположение полюсов z-преобразования в комплексной плоскости, можно сделать вывод о форме последовательности. Так наличие полюсов внутри единичной окружности соответствует затухающей или убывающей последовательности x(kDt). Полюсы на и вне единичной окружности определяют незатухающую и возрастающую последовательности x(kDt). Паре комплексно-сопряженных полюсов, соответствующих дискретному гармоническому колебанию монотонной (негармонической) последовательности, соответствуют полюса, расположенные на действительной оси.

3.1.4.3. Связь z-преобразования с преобразованием Фурье

Пусть последовательность x(kDt) имеет z-преобразование:

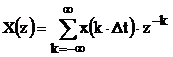Положим z=1×e^j^×^w^×^D^t, т.е. вычислим X(z) в точках, расположенных на единичной окружности в комплексной плоскости. Тогда получим:

что совпадает с дискретным рядом Фурье или преобразованием Фурье последовательности (смотри формулу 3.6). Таким образом, преобразование Фурье есть частный случай z-преобразования. Оно представляет собой z-преобразование, вычисленное на единичной оси.

Пример: Предположим, что последовательность {x(kDt)} задана своим z-преобразованием, которое имеет вид . Найдём ее комплексный спектр.

Решение: .

3.1.4.4. Свойства z-преобразования

1.Свойство линейности.

Пусть .

Тогда , где a,b-постоянные.

Данное свойство справедливо и для одностороннего z-преобразования

2. Свойство сдвига (задержки) последовательности.

Пусть 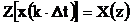и пусть .

Тогда .

Если рассматривать одностороннее z-преобразование физически нереализуемой последовательности , при -¥<k<¥, то можно показать, что .

3. Свойство умножения на показательную функцию.

Пусть .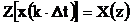

Тогда .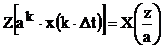

4. Свойство дифференцирования.

Пусть .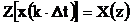

Тогда .

5. Свойство свертки последовательностей.

Пусть wk×Dt) является линейной сверткой последовательностей x(k×Dt) и y(k×Dt), т.е. , причем , .

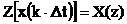Тогда .

6. Теорема о комплексной свертке.

Пусть w(k×Dt)= x(k×Dt)×y(k×Dt), причем , .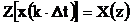

Тогда 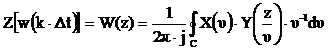, где контур интегрирования C находится внутри областей сходимости X(u) и Y(z/u).

Последнее соотношение называется теоремой о комплексной свертке, так как оно представляет z-преобразование произведения последовательностей в виде комплексной свертки их z-преобразования.

Приведённая в п.3.1.4.1 таблица и свойства z-преобразования позволяют определять z-преобразование сложных последовательностей так, как показано в нижеприведенном примере.

Пример. Пусть дана физическая реализация последовательности . Найти z-преобразование этой последовательности.

Решение. С учетом свойства линейности z-преобразования, имеем:

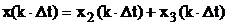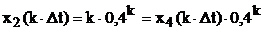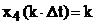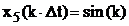В соответствии со строкой №4 таблицы находим, что

В соответствии со свойством №4 z-преобразования, имеем:

Z-преобразование x₅(k×Dt) является табличным (строка №4 таблицы). В нашем случае a=1, b=1. Отсюда, получаем:

Для нахождения x₃(k×Dt), воспользуемся свойством сдвига: определим -x₅[(k-3)×Dt] через x₅(k×Dt) следующим образом:

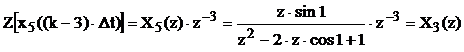Окончательно имеем:

3.1.4.5. Обратное z- преобразование

Обратное z-преобразование – это правило, которое позволяет по z-преобразованию X(z) некоторой последовательности x(k×Dt) определить вид самой этой последовательности.

Можно показать, что данное правило определяется выражением:

, (3.31)

где С − замкнутый контур, охватывающий начало координат и находящийся в области сходимости .

Вычисление контурного интеграла в формуле (3.31) может быть выполнено с помощью теоремы о вычетах, в соответствии с которой интеграл по замкнутому контуру от функции f(z) равен сумме вычетов в полюсах f(z), охваченных этим контуром, умноженной на 2pj:

(3.32)

Для того, чтобы воспользоваться этой теоремой, нужно знать определения вычета. Напомним его. Пусть некоторая функция f(z) комплексной переменной z имеет L полюсов: p₁, p₂,..., p_L, причем i-тый полюс имеет кратность m. Вычетом функции f(z) в точке z=p_i называется выражение

. (3.33)

Положив в (3.31) f(z)=X(z)×z^k^-1 с помощью соотношений (3.32) и (3.33), можно определить x(k×Dt).

Возможен и другой подход, при котором функция X(z) различными способами (например, с помощью разложения на простые дроби) с использованием свойств z-преобразования представляется в виде линейных комбинации элементарных табличных z-преобразований, оригиналы которых можно определить с помощью таблицы приведённой в п.3.1.4.1.

3.1.5. Конечные разности и разностные уравнения

Пусть имеем последовательность x(k×Dt), изображенную на рисунке 1:

Рисунок 1

Скорость изменения этой последовательности характеризуется ее первой конечной разностью, которая является дискретным аналогом первой производной непрерывной функции x(t), дискретными отсчетами которой является последовательность x(k×Dt).

Первая разность D₁x(k×Dt)= x(k×Dt)-x[(k-1) ×Dt] (см. рисунок 1):

Рисунок 5.2

Кроме первой разности существуют вторая, третья и т.д. конечные разности, аналогичные второй, третьей и т.д. производной непрерывной функции x(t):

D₂x(k×Dt)= D₁x(k×Dt)- D₁[(k-1)Dt]=x(k×Dt)-x[(k-1)Dt]-x[(k-1)Dt]+x[(k-2)Dt]=

=x(k×Dt) −2x[(k-1)Dt]+x[(k-2)Dt].

Как видно из этого равенства, конечные разности высшего порядка могут быть выражены непосредственно через отсчеты последовательности. При этом порядок конечной разности определяет максимум задержки отсчета последовательности, присутствующей в этом выражении.

Соотношение между последовательностями x(k×Dt), y(k×Dt) и их конечными разностями различных порядков называется разностным уравнением. Разностное уравнение может быть записано в виде:

a_MD_My(k×Dt)+ a_M-1D_M-1y(k×Dt)+...+ a₁D₁y(k×Dt)+ a₀y(k×Dt)==x(k×Dt). (3.34)

Порядок M наивысшей конечной разности определяет порядок данного уравнения. Поскольку все конечные разности (в том числе и разность нулевого порядка y(k×Dt)) входят в данное уравнение первой степени, оно называется линейным. В том случае, когда a₀, a₁,..., a_M не меняются во времени, имеем разностное уравнение с постоянными коэффициентами. Если x(k×Dt)=0, уравнение (3.34) превращается в однородное разностное уравнение. Последовательность x(k×Dt) также может быть задана в виде однородного разностного уравнения:

b_ND_Nx(k×Dt)+ b_N_-1D_N-1x(k×Dt)+...+ b₁D₁x(k×Dt)+ b₀x(k×Dt)=0,

откуда

Подставляя это в (3.34), имеем:

Если подставить в полученное уравнение значение конечных разностей различных порядков, выраженных непосредственно через отсчеты последовательностей, то получим выражение, связывающее между собой обе последовательности в виде:

(3.35)

Выражение (3.35) представляет собой форму записи разностного уравнения, традиционно используемую при описании дискретных линейных систем.

§ 3.2. Дискретные линейные системы

3.2.1. Общие понятия и определения

Дискретной системой называется алгоритм преобразования одной последовательности {x(k×Dt)}, называемой входной, в другую {y(k×Dt)}, называемую выходной. В общем случае, это можно записать в виде:

y(k×Dt)=j_дп{x(k×Dt)},

где j_дп- оператор дискретного преобразования.

Особенностью этого определения является то, что дискретными системами названо не устройство, а алгоритм. Это обусловлено тем, что дискретная система может быть реализована программно.

Пусть {x₁(k×Dt)} и {x₂(k×Dt)} – произвольные входные последовательности, а y₁(k×Dt)=j_дп{x₁(k×Dt)} и y₂(k×Dt)=j_дп{x₂(k×Dt)} – соответствующие им отклики системы. Тогда дискретная система называется линейной, если для произвольных постоянных a и b справедливо равенство:

Ф_дп{a×x₁(k×Dt)+ b×x₂(k×Dt)}=a×y₁(k×Dt)+b×y₂(k×Dt).

Линейная дискретная система является системой с постоянными параметрами (ЛПП), если ее свойства не изменяются во времени и одинаковы в два произвольных момента времени (k-k₀)×Dt и k×Dt при любом k₀.

ЛПП называется каузальной, если ее отклик при k= k₀ зависит только от отсчетов входной последовательности, появившихся до момента k₀×Dt.

ЛПП называется устойчивой, если при любой ограниченной по уровню входной последовательности, ее выходная последовательность тоже будет ограничена по уровню для любого k.

3.2.2. Временные характеристики и алгоритм ЛПП

Алгоритмом ЛПП называется правило, позволяющее определить отклик системы по ее входной последовательности и характеристике системы. Основными временными характеристиками ЛПП является импульсная реакция (характеристика) и переходная характеристика.

Импульсная реакция h(k×Dt) – это последовательность на выходе ЛПП, полученная путем воздействия на вход последовательности единичный отсчет x₀(k×Dt) (см. формулу (3.2)). Импульсная реакция может иметь конечное или бесконечное число ненулевых отсчетов. В первом случае имеем ЛПП с КИХ-фильтром (фильтр с конечной импульсной характеристикой), во втором случае – БИХ-фильтр (фильтр с бесконечной импульсной характеристикой).

Переходной характеристикой g(k×Dt) называется последовательность на выходе ЛПП, при воздействии на ее вход последовательности единичный скачок x₁(k×Dt) (см. формулу (3.3)).

Можно показать, что отсчеты выходной последовательности определяются как бесконечная свёртка отсчетов входной последовательности и импульсной реакции фильтра h(k×Dt) (в общем случае, когда h(k×Dt), y(k×Dt), x(k×Dt) являются некаузальными последовательностями и содержат бесконечное число ненулевых отсчетов), которая имеет вид:

. (3.36)

В том случае, когда x(k×Dt) и h(k×Dt) являются бесконечными каузальными последовательностями, т.е. когда x(k×Dt)=0, k<0, h(k×Dt)=0, k<0 выражение (3.36) преобразуется в линейную свертку:

(3.37)

Если же h(k×Dt) – последовательность конечной длины, содержащая M+1 отсчет, то выражение (3.37) трансформируется к виду:

. (3.38)

При k£M конечная свертка вычисляется так же, как и линейная свертка. При k>M в сумме учитывается лишь текущий отсчет x(k×Dt) и M ему предшествующих. С помощью соотношения (3.37) нетрудно найти связь между импульсной реакцией и переходной характеристикой системы:

Выражения (3.36), (3.37) и (3.38) определяют временной алгоритм ЛПП, связывающий отсчеты входной последовательности, импульсную реакцию ЛПП и выходную последовательность. Временной алгоритм ЛПП также может быть задан в виде разностного уравнения. В общем случае это уравнение выглядит так:

, (3.39)

где a_mи b_n – некоторые действительные коэффициенты, набор которых можно также рассматривать как временную характеристику ЛПП. В частном случае, все коэффициенты a_m могут быть нулевыми; в этом случае имеем:

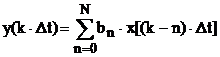. (3.40)

Сопоставляя выражения (3.40) и (3.38), можно заключить, что коэффициенты b_n равны соответствующим отсчетам (при n=k) импульсной реакции h(k×Dt). Как уже отмечалось, алгоритм (3.38), а, следовательно, и (3.40), предполагает, что ЛПП имеет конечную импульсную реакцию. Таким образом, для КИХ-фильтров коэффициент разностного уравнения совпадает с отсчетами импульсной реакции.

Можно показать, что системе, описываемой разностным уравнением общего вида (3.39) соответствует алгоритм (3.37) линейной свертки, оперирующей с бесконечной импульсной реакцией. Связь между коэффициентами разностного уравнения и отсчетами импульсной реакции здесь более сложная.

ЛПП-системы, временной алгоритм которых описывается линейной сверткой или разностным уравнением общего вида и имеющие бесконечную импульсную характеристику, называются рекурсивными. Они характеризуются тем, что для расчета очередного выходного отсчета требуются не только входные, но и предшествующие выходные отсчеты. Поэтому такие системы имеют обратные связи.

ЛПП-системы, временной алгоритм которых описывается конечной сверткой или усеченным разностным уравнением и имеющие конечную импульсную характеристику, называются нерекурсивными. Они характеризуются тем, что для получения очередного отсчета требуются только входные отсчеты, поэтому обратных связей в них нет.

По импульсной характеристике системы можно судить о ее физической реализуемости и устойчивости. Система является физически реализуемой если её импульсная характеристика представляет собой физически реализуемую последовательность. Необходимым и достаточным условием устойчивости системы является следующее требование к импульсной характеристике

. (3.41)

Поскольку импульсная характеристика любой нерекурсивной системы является последовательностью конечной длины, в этом случае сумма в левой части неравенства (3.41) содержит конечное число ненулевых слагаемых и, следовательно, неравенство (3.41) всегда выполняется. Т.о, нерекурсивные системы всегда устойчивы.

3.2.3. Частотные характеристики и алгоритм ЛПП

Пусть на входе ЛПП действует последовательность x(k×Dt)=e^j^×^w^×^k^×^D^t – дискретная комплексная экспонента. Если импульсная реакция системы есть h(k×Dt), то в соответствии с временным алгоритмом (3.36) выходная последовательность системы:

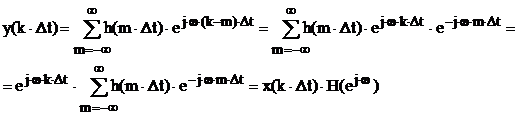
Таким образом, преобразование элементарной гармонической последовательности линейной дискретной системой описывается как умножение этой последовательности на частотно зависящий комплексный множитель H(e^j^×^w). Этот множитель выражается через импульсную реакцию следующим образом:

(3.42)

Величину H(e^j^×^w) называют комплексной частотной характеристикой (КЧХ) системы, поскольку она определяет, каким образом изменяются параметры элементарной комплексной гармонической составляющей, прошедшей через систему. Сравнивая выражения (3.42) и (3.6), можно заключить, что H(e^j^×^w) есть преобразование Фурье или комплексный спектр импульсной реакции системы h(k×Dt). В связи с этим можно отметить, что H(e^j^×^w) есть комплексная периодическая функция частоты с периодом w_дискр=2p×t_дискр=2p/Dt. Модуль функции H(e^j^×^w) представляет собой амплитудно-частотную характеристику (АЧХ) ЛПП-систем, а аргумент этой функции – фазо-частотную характеристику (ФЧХ).

АЧХ и ФЧХ ЛПП могут выглядеть так, как показано на рисунке.

Рисунок

Из рисунка видно, что АЧХ является четной функцией частоты, а ФЧХ является нечетной функцией частоты. Это следует из свойства симметрии дискретного преобразования Фурье. В соответствии со свойством симметрии, на интервале 0...w_д АЧХ будет симметрична относительно w_д/2. Аналогично, ФЧХ будет антисимметрична на интервале 0...w_д относительно w_д/2. Поэтому интервал от 0 до w_д/2 называется главным значением периода частотной характеристики. Поэтому, ввиду периодичности и симметрии достаточно определить значение АЧХ и ФЧХ только на этом интервале.

В общем случае, на вход системы может быть подана произвольная последовательность {x(k×Dt)}. При этом, на выходе системы появится последовательность {y(k×Dt)}, которая в соответствии с (3.37) является результатом линейной свертки последовательностей {x(k×Dt)} и {h(k×Dt)}. Поскольку преобразование Фурье или комплексный спектр последовательности можно рассматривать как частный случай z-преобразования, то все свойства z-преобразования распространяются и на преобразование Фурье. Как известно, z-преобразование линейной свертки двух последовательностей равно произведению z-преобразований этих последовательностей. Поэтому комплексный спектр выходной последовательности:

Y(e^j^×^w)=X(e^j^×^w)×H(e^j^×^w), (3.43)

где X(e^j^×^w) – комплексный спектр входной последовательности.

Равенство (3.43) выражает частотный алгоритм ЛПП.

3.2.4. Передаточная функция ЛПП

Передаточная функция ЛПП представляет собой z-преобразование импульсной реакции системы:

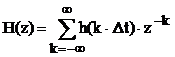. (3.44)

Передаточная функция H(z), вычисленная на единичной окружности, (т.е. при подстановке z=exp(jwDt)) превращается в КЧХ системы и определяет частотные свойства системы. Используя свойства z-преобразования свертки двух последовательностей и учитывая выражение (3.37) можно записать z-алгоритм ЛПП:

Y(z)=X(z)×H(z), (3.45)

где X(z) и Y(z) – z-преобразование выходной и входной последовательностей.

Положим, что временной алгоритм ЛПП задан разностным уравнением вида (3.39). Найдем связь между передаточной функцией ЛПП и коэффициентами разностного уравнения. Возьмем z-преобразование от обеих частей (3.39), пользуясь свойствами линейности и сдвига:

Отсюда имеем:

С учетом (3.45) получим:

. (3.46)

Полученное выражение определяет взаимосвязь передаточной функции рекурсивной ЛПП с коэффициентами, описывающими его разностное уравнение.

Для нерекурсивного ЛПП все коэффициенты a_m равны нулю, поэтому выражение (3.46) примет вид:

. (3.47)

Полученное соотношение показывает, что передаточная функция нерекурсивного ЛПП имеет единственный N-кратный полюс в точке z=0. По передаточной функции системы можно судить о ее физической реализуемости и устойчивости. Так можно показать, что если в выражении (3.46) N-M£0 или N£M, то описываемая этим выражением рекурсивная ЛПП является физически реализуемой. Поскольку у нерекурсивных систем импульсная реакция представляет собой последовательность конечной длины, то такие системы путем сдвига на соответствующее число отсчетов h(k×Dt) могут быть сделаны физически реализуемыми. Критерием устойчивости выражения для передаточной функции является расположение ее полюсов. Если все полюсы передаточной функции располагаются внутри единичной окружности, то соответствующая ей импульсная реакция будет затухающей последовательностью. Поэтому будет выполняться условие (3.41) и система будет устойчивой. У нерекурсивных систем h(k×Dt) представляет собой последовательность конечной длины, т.е. условие (3.41) всегда выполняется. Передаточная функция нерекурсивного фильтра имеет один N-кратный полюс в точке z=0, т.е. внутри единичной окружности, поэтому нерекурсивные ЛПП всегда устойчивы.

3.2.5. Построение структурных схем дискретных систем

Структурная схема дискретной системы может быть построена по ее математической модели: разностному уравнению или передаточной функции. Структурная схема позволяет описать процесс обработки сигналов в цифровых фильтрах от момента принятия текущего k-го отсчета обрабатываемого сигнала, до момента принятия (k+1)-го отсчета. Т.о. удается графически изобразить временной алгоритм работы ЛПП. Решение задачи построения структурной схемы неоднозначно. Оказывается, что одну и ту же передаточную функцию или одно и то же разностное уравнение можно реализовать с помощью различных структур. При этом разные структуры будут иметь и несколько различные свойства. Дело в том, что практическая реализация цифрового фильтра сопряжена с появлением ряда специфических погрешностей, которые не учитываются при описании ЛПП как линейной системы с помощью разностного уравнения или передаточной функции. Такие погрешности возникают вследствие ограниченной точности представления коэффициентов разностного уравнения, определяющего фильтр, отсчетов входного сигнала, а также результатов арифметических операций, выполняемых в фильтрах. Эти погрешности по-разному проявляются в различных структурах, соответствующих одной и той же передаточной функции. Выбор структуры оказывает влияние на шумы и динамический диапазон цифрового фильтра, точность воспроизведения характеристик при ограниченной длине кодового слова, представляющего коэффициенты фильтра, а также на реализационные затраты при построении фильтра.

3.2.5.1. Построение структурных схем ЛПП по разностному уравнению

Логика построения структурных схем ЛПП наиболее отчетливо проявляется в том случае, когда в качестве математической модели ЛПП используется описание ее с использованием разностного уравнения. Пусть, например, имеем рекурсивный ЛПП 1-го порядка, описываемый уравнением:

y(k×Dt)=a₁×y[(k-1)×Dt]+b₀×x(k×Dt)+b₁×x[(k-1)×Dt].

Это уравнение показывает, что для получения текущего отсчета выходной последовательности нужно:

1) умножить на b₀ текущий отсчет входной последовательности x(k×Dt);

2) умножить на b₁ предшествующий отсчет входной последовательности x(k×Dt);

3) умножить на a₁ предшествующий отсчет выходной последовательности y(k×Dt);

4) результаты сложить.

Для того чтобы иметь в момент сложения предшествующие отсчеты x[(k-1)×Dt] и y[(k-1)×Dt] нужно задержать или запомнить на один такт отсчеты x(k×Dt) и y(k×Dt), появившиеся Dt секунд тому назад. Т.о. получается следующая схема ЛПП:

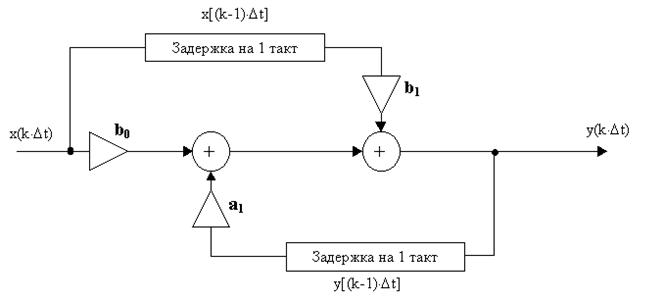
Рисунок 1

В данном примере была рассмотрена рекурсивная ЛПП, описываемая разностным уравнением общего вида. Очевидно, что совершенно аналогичным образом можно построить структурную схему нерекурсивной ЛПП, описываемой усеченным разностным уравнением. В этом случае в схеме будут отсутствовать обратные связи.

3.2.5.2. Построение структурных схем ЛПП по передаточной функции

Можно выделить три основных способа построения структурных схем ЛПП по передаточной функции H(z):

1) прямой;

2) параллельный;

3) последовательный.

Прямой способ основан на использовании H(z) заданной непосредственно в виде (3.46) или (3.47). По этим выражениям можно восстановить ЛПП, описываемый разностным уравнением вида (3.39) или (3.40). По этому уравнению можно построить структурную схему. Структурную схему можно построить непосредственно по виду выражения (3.46) или (3.47). При этом следует помнить, что числитель выражения (3.46) определяет структуру прямых ветвей ЛПП, а знаменатель – структуру ветвей обратной связи, коэффициенты a_m и b_n являются множителями, а символ z^-ⁱ означает задержку на i тактов.

Структурная схема имеет вид:

Рисунок 2

Данная структура соответствует рекурсивной ЛПП и называется прямой формой 1. На практике прямую форму 1 применяют редко из-за большого числа элементов задержки и сумматоров.

Для нерекурсивных ЛПП получим схему изображенную на рисунке 3.

Рисунок 3

Как видно изрис.3, эта схема представляет собой линию задержки с отводами. Цифровой фильтр, имеющий такую структуру, называется транверсальным фильтром.

Она также называется прямой формой. Для нерекурсивных фильтров существует только одна прямая форма.

Для рекурсивных фильтров существует прямая форма 2. Для того чтобы перейти к ней, представим передаточную функцию, заданную в виде (3.46), в форме произведения передаточных функций двух ЛПП:

где

	,
	.

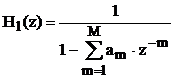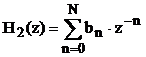Произведению передаточных функций двух фильтров соответствует последовательное включение этих фильтров. Обозначим последовательность на входе рекурсивного фильтра как w(k×Dt), которая является выходной для фильтра с передаточной функцией H₁(z). Тогда пользуясь формулами (3.46) и (3.39) можно записать разностное уравнение, описывающее работу 1-го фильтра:

Аналогично на базе формул (3.47) и (3.40) с использованием выражения для H₂(z) имеем:

Полученные разностные уравнения позволяют построить структурную схему фильтра с передаточной функцией H(z) в виде:

Рисунок 4

Очевидно, что при N=M можно использовать один набор элементов задержки.

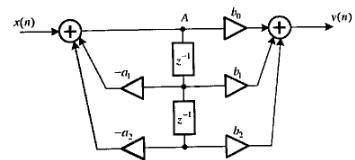
Полученная структура называется прямой формой 2 или канонической. Она характеризуется тем, что используется минимальное число элементов задержки и сумматоров. Для нерекурсивных фильтров прямой формы 2 не существует.

Если передаточную функцию ЛПП представить в виде суммы простых дробей (разложить на простые дроби), то она будет определяться выражением:

где H_i(z) – звенья 1-го и 2-го порядка, L – число звеньев.

Такое представление передаточной функции является математическим основанием для построения параллельной структуры, имеющей вид:

Рисунок 5

Параллельные структуры существуют только для рекурсивных ЛПП. Если передаточная функция ЛПП представлена в виде произведения передаточных функций отдельных звеньев

то получаем математическое основание для построения последовательной структуры.

Рисунок 6

Элементарные звенья с передаточной функцией H_i(z) представляют собой ЛПП 1-го и 2-го порядка.

Реализация звеньев H_i(z) осуществляется на основе прямой формы 2 для рекурсивных систем и прямой формы для нерекурсивных. Последовательные структуры существуют как для рекурсивных, так и для нерекурсивных систем.

Дата добавления: 2018-02-15; просмотров: 3939; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 67

Мы поможем в написании ваших работ!