Графическая иллюстрация вычисления ДПФ 8-точечной последовательности на основе быстрого преобразования Фурье
Проиллюстрируем графически процесс нахождения ДПФ восьмиточечной последовательности с помощью рассмотренного алгоритма БПФ. При этом для вычисления искомого 8-точечного ДПФ X(ejωn) нужно определить два 4-точечннх ДПФ X1(ejωn) и X2(ejωn) последовательностей {x1(k∆t)} и {x2(k∆t)} (см. рисунок 2, левая половина). Затем с помощью формулы (3.23) можно вычислить отсчеты X(ejωn). Для графической иллюстрации данного процесса примем обозначения, показанные на рисунке 1.
Незачерченные кружки означают операцию "сложение - вычитание", причем верхнему выходу соответствует сумма, а нижнему - разность. Стрелка показывает умножение на значение множителя, указанного около нее. С учетом этих обозначений процесс вычисления ДПФ в рассматриваемом случае выглядит так, как показано на рисунке 2.
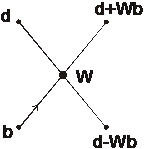
Рисунок 1
Но 4-точечные ДПФ последовательностей X1(ejωn) и X2(ejωn) могут быть также вычислены с помощью БПФ. Каждая из последовательностей {x1(k∆t)} и {x2(k∆t)} при этом в свою очередь разбивается на две последовательности: {x1(k∆t)} на {a(k∆t)} и {b(k∆t)}, а {x2(k∆t)} на {c(k∆t)} и {d(k∆t)}, состоящие соответственно из четных и нечетных членов. Аналогично по формулам (3.23) можно вычислить значения 4-точечных ДПФ X1(ejωn) и X2(ejωn). При этом формулы (3.23) будут выглядеть, например для X1(ejωn) так:
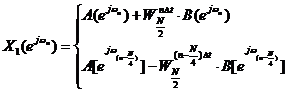
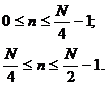
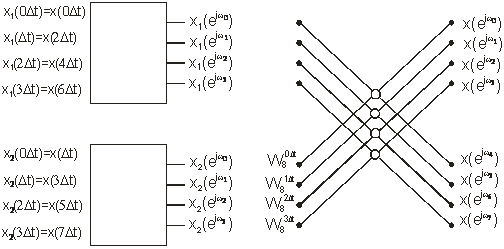
Рисунок 2
Поскольку при вычислении 8-точечного ДПФ фигурировал множитель WN (N=8), т.е. его значения уже были вычислены, для уменьшения общих значений целесообразно, чтобы и в последних формулах присутствовал этот же множитель. Как уже было показано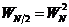 
, поэтому
|
|
|
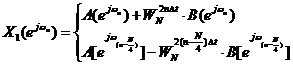
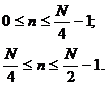
Аналогично можно записать в подобные формулы для вычисления X2(ejωn) через С(ejωn) и D(ejωn).
Двухточечные ДПФ A(ejωn), B(ejωn), C(ejωn) и D(ejωn) также могут быть вычислены с помощью базовых операций БПФ, обозначаемых типовым графом, показанном на рисунке 1. Действительно, применяя формулу ДПФ для вычисления, например A(ejωn) имеем:
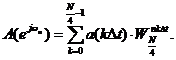
Учитывая, что WN/4=WN4, можно записать:
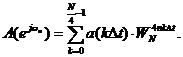
Подставляя в эту формулу обозначения a(0) и a(∆t), выраженные через отсчеты исходной последовательности {x(k∆t)}, в нашем случае имеем:
,
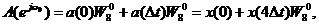
так как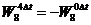 
.
Аналогично можно записать подобные формулы для вычисления X2(ejωn) через C(ejωn) и D(ejωn).
Структура полученных формул аналогична структуре выражений (3.23) и соответствует базовым операциям алгоритма БПФ.
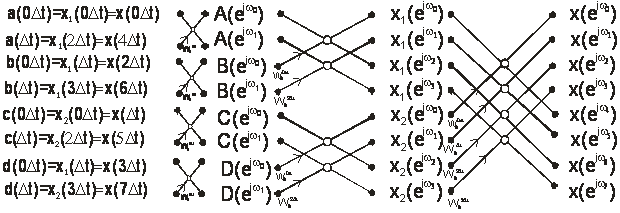
Рисунок 3
Полный граф вычисления 8-точечного ДПФ последовательности {x(k∆t)} с помощью рассмотренного алгоритма БПФ, построенный на основе приведенных рассуждений, представлен на рисунке 3.
Анализ построенного графа показывает, что на каждом этапе БПФ, т.е. при каждом сокращении размеров ДПФ, необходимо выполнить N/2 комплексных умножений. Поскольку общее количество этапов равно log2N, то число комплексных умножений приблизительно равно (N/2) log2N. Приблизительно потому, что умножение на WN∆t=1; WN(N/2)∆t=-1; WN(N/4)∆t=-j; WN(3N/4)∆t=+j в действительности сводится просто к сложениям и вычитаниям комплексных чисел (как в рассматриваемом примере). Однако для больших N фактическое число умножений определяется названным числом.
|
|
|
Считается, что эффективно применение БПФ, начиная с N=128. При этом число комплексных умножений сокращается с 214=16384 (вычисление ДПФ без БПФ) до 448.
Дополнительной особенностью алгоритма БПФ, обуславливающей удобство его использования при вычислениях, является то, что он состоит из однотипных повторяющихся операций.
Разработаны алгоритмы БПФ и для N, не равного целой степени 2. Простейшим приемом в этом случае является дополнение исходной последовательности нулевыми отсчетами до ближайшего числа, равного целой степени 2, возможны и другие подходы . Но в любом случае выигрыш в сокращении объема вычислений в данной ситуации является меньшим.
Дата добавления: 2018-02-15; просмотров: 877; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!