Дискретное преобразование Фурье периодической последовательности.
Рассмотрим теперь периодическую последовательность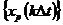 
, с помощью которой мы будем описывать сигнал, полученный в результате дискретизации периодического непрерывного процесса с периодом 
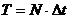, где 
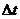– шаг дискретизации; N – количество отсчетов последовательности, укладывающихся в интервале Т.
Рисунок 2.6
Величина N является периодом последовательности 
.
Можно показать, что комплексный спектр 
такой последовательности связан с её отсчётами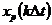 
соотношением
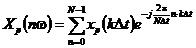, (3.10)
а обратная зависимость, позволяющая по отсчётам спектра определить отсчёты последовательности , имеет вид
. (3.11)
Сравнивая выражения (3.10) и (3.6) можно заключить, что они становятся внешне идентичными, если в (3.10) ввести обозначени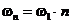е 
, где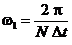 
можно трактовать как круговую частоту первой гармоники. Данное сопоставление показывает, что в отличие от 
спектр периодической последовательности существует лишь на дискретных частотах 
, кратных частоте первой гармоники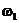 
, т.е. является не сплошным, а дискретным. При этом спектр (как и спектр любого дискретизированного с шагом 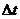сигнала) также является периодичным с периодом 
и в его периоде содержится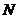 
отсчётов, соответствующих частотам 
.
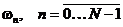Выражение (3.10) называют дискретным преобразованием Фурье (ДПФ), а выражение (3.11) обратным дискретным преобразованием Фурье (ОДПФ) периодической последовательности.
|
|
|
Итак, если временная последовательность имеем период 
из N отсчетов, то ее комплексный спектр представляет собой периодическую последовательность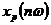 
в частотной области с периодом 
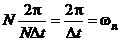, также содержащим N отсчетов,
Дискретное преобразование Фурье последовательности конечной длины
Рассмотрим последовательность конечной длины 
, 
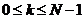, содержащую N отсчетов. Предположим, что она совпадает с одним из периодов некоторой периодической последовательности 
.
В соответствии с (3.6) ее сплошной периодический спектр будет определяться как (рисунок а):
,
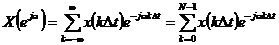так как .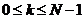
Найдем N значений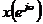 
в равноудаленных точках частотной оси 
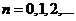(рисунок б)
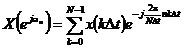(3.12)
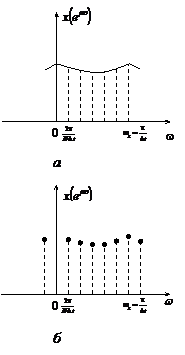
Рисунок
Но на интервале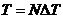 
отсчеты последовательности конечной длины совпадают с отсчетами периодической последовательности , т.е.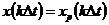 
. Поэтому, сравнивая последние выражения с (3.10), можно заключить, что значения спектра последовательности конечной длины в дискретных точках 
при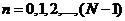 
будут равны отсчетам ДПФ периодической последовательности , получаемой периодическим повторением . Совокупность отсчетов непрерывного периодического спектра последовательности , определяемая выражением (3.12), называется ДПФ последовательности конечной длины.
|
|
|
По аналогии с (3.11) можно ввести понятие ОДПФ последовательности конечной длины:
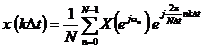(3.13)
Отсюда следует, что достаточно знать только частичное описание спектра последовательности конечной длины, т.е. ее ДПФ, чтобы точно описать эту последовательность, используя ее ОДПФ.
Но так как ДПФ с помощью ОДПФ позволяет восстановить исходную последовательность конечной длины, то, пользуясь дискретным рядом Фурье, можно затем точно восстановить и весь сплошной спектр . Иначе говоря, непрерывный спектр полностью определяется своими дискретными отсчетами, представляющими собой ДПФ последовательности конечной длины 
.
3.1.2.4. N-точечное ДПФ последовательности. Вычисление N-точечного ДПФ L-точечной последовательности при N<L.
При введении понятия ДПФ последовательности конечной длины, содержащей N отсчетов, мы дискретизировали ее сплошной спектр в N равноудаленных точках частотной оси. Однако в принципе возможна и другая ситуация, когда размер (число отсчетов) ДПФ N не совпадает с числом ненулевых отсчетов L исследуемой последовательности (возможен случай, когда 
L = ∞). Получаемая при этом совокупность отсчетов спектра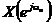 
, вычисленных на частотах
|
|
|
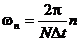(3.14)
называется N-точечным ДПФ последовательности.
Для определения N-точечного ДПФ можно воспользоваться дискретным рядом Фурье (3.6), предварительно вычислив частоты взятия выборок с помощью (3.14). Однако же в тех случаях, когда N > L данную задачу можно решить и непосредственно на основе выражения для ДПФ (3.12). При этом поступают так:
1. Дополняют исследуемую последовательность до N отсчетов, приписав к ней N – L ненулевых отсчетов;
2. С помощью формулы (3.12) определяют ДПФ дополненной последовательности, которое и будет представлять собой искомые значения N-точечного ДПФ.
Формула (3.12) при этом преобразуется к виду
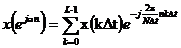
Суммирование здесь ведется в пределах от 0 до L - 1, так как остальные (N - L) отсчетов дополненной последовательности равны 0.
Дата добавления: 2018-02-15; просмотров: 948; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!