Задание 2.6. Решить уравнения, применяя метод неопределённых коэффициентов.

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Вар.	Уравнение	Вар.	Уравнение
2.6.1.	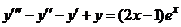.	2.6.16.	.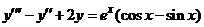
2.6.2.	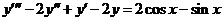.	2.6.17.	.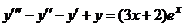
2.6.3.	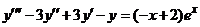.	2.6.18.	.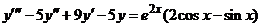
2.6.4.	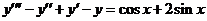.	2.6.19.	.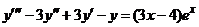
2.6.5.	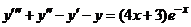.	2.6.20.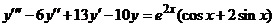
2.6.6.	.	2.6.21.	.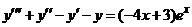
2.6.7.	.	2.6.22.	.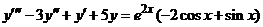
2.6.8.	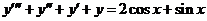.	2.6.23.	.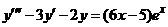
2.6.9.	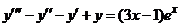.	2.6.24.	.
2.6.10.	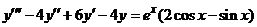.	2.6.25.	.
2.6.11.	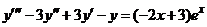.	2.6.26.	.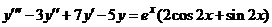
2.6.12.	.	2.6.27.	.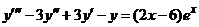
2.6.13.	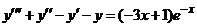.	2.6.28.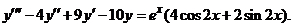
2.6.14.	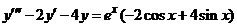.	2.6.29.	.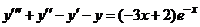
2.6.15.	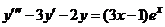.	2.6.30.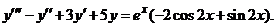

Для линейного неоднородного уравнения 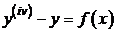найти общее решение, используя метод неопределенных коэффициентов для нахождения частного решения.

Вар.		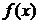Вар.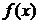
2.6.31.	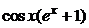.	2.6.46.	.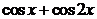
2.6.32.	.	2.6.47.	.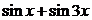
2.6.33.	.	2.6.48.	.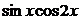
2.6.34.	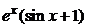.	2.6.49.	.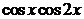
2.6.35.	.	2.6.50.	.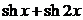
2.6.36.	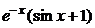.	2.6.51.	.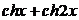
2.6.37.	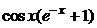.	2.6.52.	.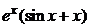
2.6.38.	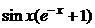.	2.6.53.	.
2.6.39.	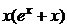.	2.6.54.	.
2.6.40.	.	2.6.55.	.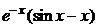
2.6.41.	.	2.6.56.	.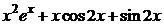
2.6.42.	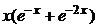.	2.6.57.	.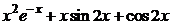
2.6.43.	.	2.6.58.	.
2.6.44.	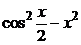.	2.6.59.	.
2.6.45.	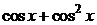.	2.6.60.	.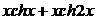

2.7. Применение дифференциальных уравнений 2-го порядка для
решения геометрических задач

Из курса математического анализа известно, что производная 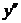функции применяется для исследования геометрических свойств линий, а именно: выпуклость (вверх и вниз) и кривизна линии. Кривизна линии характеризует скорость вращения касательной к кривой при движении точки по кривой.

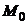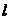
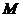Пусть есть угол, на который поворачивается касательная при переходе из точки кривой линии в точку , а 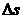− длина части кривой между названными точками. Тогда величина 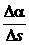выражает среднюю кривизну дуги 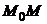. Величина 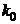= 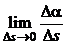называется кривизной кривой 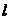, а величина 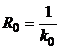радиусом кривизны кривой 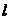в точке .

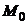Для окружности кривизна величина постоянная и равна 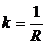, где – радиус окружности. Чем меньше радиус, тем больше кривизна. Последнюю формулу легко получить из того, что длина 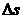любой дуги окружности равна 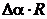, где − радиус окружности, – центральный угол, опирающийся на дугу (центральный угол, опирающийся на дугу окружности равен углу между касательными, проведенными к дуге окружности в её концах).

На рис.2.1 показана окружность радиуса для точки 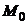кривой. Учитывая смысл предельного перехода, заметим, что кривую 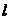в окрестности точки 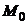можно заменить соприкасающейся окружностью радиуса . Центр этой окружности располагается на нормали кривой в данной точке, причём в той же полуплоскости относительно касательной, что и рассматриваемая кривая.

В математическом анализе для вычисления кривизны линии в каждой её точке получена формула 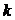= 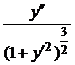. Это значит, что радиус кривизны = .

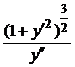Известно, что для линий, выпуклых вниз, производная 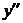>0. Для таких лини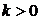й и , что согласуется с чертежом. Соответственно, для линий, выпуклых вверх − 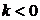и . Учитывая замеченное свойство кривых линий, удобно определить проекцию радиуса кривизны на ось формулой 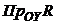= 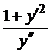, что отражает направление радиуса кривизны вдоль нормали кривой для рассматриваемой точки.

Пример 2.12. Найти уравнение линии, для которой проекция радиуса кривизны на ось равна 1.

Решение. 1) Учитывая условие задачи: 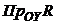=1, запишем дифференциальное уравнение, соответствующее требуемым геометрическим свойствам линии или .

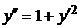2) Дифференциальное уравнение 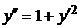решаем способом понижения порядка, принимая 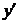= . Тогда 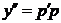. Перепишем уравнение 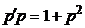, или . Интегрируя это уравнение, получаем 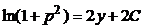, или .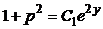

3) Так как 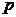= 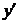, из выражения 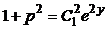следует 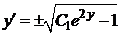. Учитывая, что 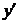= 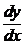, получим уравнение . При вычислении интеграла левой части применяем способ замены переменных. В результате получим .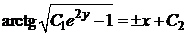

Замечание. Выражение общего решения можно преобразовать к виду более удобному для применения в задачах Коши .

Ответ.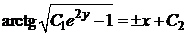, или .

Дата добавления: 2018-02-15; просмотров: 656; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!