Метод вариации произвольных постоянных решения неоднородных дифференциальных уравнений
Линейные дифференциальные уравнения
Линейные однородные дифференциальные уравнения 2-го порядка
Пусть задано однородное дифференциальное уравнение 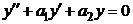 с постоянными коэффициентами
с постоянными коэффициентами 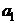 ,
, 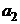 и необходимо найти его общее решение.
и необходимо найти его общее решение.
Приведем алгоритм решения этой задачи:
1) Ищем фундаментальные решения уравнения в виде функций 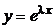 . Подставляя
. Подставляя 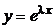 и её производные
и её производные 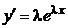 и
и 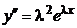 в заданное уравнение, получаем, что числа
в заданное уравнение, получаем, что числа 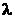 должны быть корнями характеристического уравнения
должны быть корнями характеристического уравнения 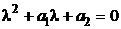 .
.
2). Находим корни характеристического уравнения  ,
,  и строим фундаментальную систему решений (ФСР):
и строим фундаментальную систему решений (ФСР):
а) если  ,
,  − действительные различные, ФСР образуют функции
− действительные различные, ФСР образуют функции 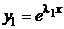 и
и 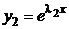 ;
;
б) если  ,
,  − действительные и равные, ФСР образуют функции
− действительные и равные, ФСР образуют функции 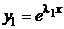 и
и 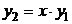 ;
;
в) если 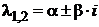 − комплексно сопряжённые, ФСР образуют функции
− комплексно сопряжённые, ФСР образуют функции 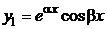 и
и  .
.
3). Имея ФСР, записываем общее решение заданного уравнения 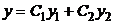 , где
, где 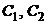 произвольные постоянные.
произвольные постоянные.
Если необходимо решить задачу Коши, то есть найти функцию  , которая является решением дифференциального уравнения и удовлетворяет заданным начальным условиям
, которая является решением дифференциального уравнения и удовлетворяет заданным начальным условиям 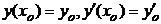 , то подставляя условия
, то подставляя условия 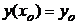 ,
,  в выражения
в выражения 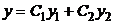 и
и 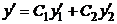 , получаем систему линейных уравнений относительно
, получаем систему линейных уравнений относительно 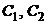 для нахождения частного решения, удовлетворяющего заданным начальным условиям. Решая её, находим решение задачи Коши.
для нахождения частного решения, удовлетворяющего заданным начальным условиям. Решая её, находим решение задачи Коши.
Пример 2.1: Решить задачу Коши: 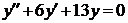 ,
,  . Записать общее решение и соответствующее заданным начальным условиям частное решение.
. Записать общее решение и соответствующее заданным начальным условиям частное решение.
Решение. 1) По заданному дифференциальному уравнению составляем характеристическое уравнение 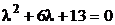 .
.
|
|
|
2) Находим корни характеристического уравнения  .
.
3) Имея характеристические корни, составим ФСР  =
= 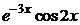 ,
,  =
= 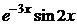 .
.
4) Имея ФСР, запишем общее решение дифференциального уравнения  .
.
5) Из общего решения находим
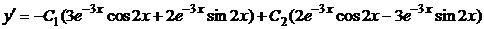 .
.
6) Используя полученные выражения  и
и 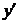 , для заданных начальных условий получим систему
, для заданных начальных условий получим систему 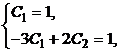 из которой
из которой 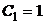 ,
, 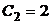 .
.
7) Запишем частное решение (решение задачи Коши) 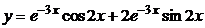 .
.
Ответ. Общее решение:  , частное решение:
, частное решение: 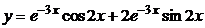 .
.
Пример 2.2. Решить задачу Коши 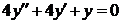 , если
, если  . Записать общее решение и соответствующее заданным начальным условиям частное решение.
. Записать общее решение и соответствующее заданным начальным условиям частное решение.
Решение. 1) Составляем характеристическое уравнение 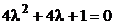 .
.
2) Найдём корни характеристического уравнения 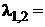 –
– 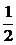 , то есть имеем кратные корни.
, то есть имеем кратные корни.
3) Составляем ФСР  =
= 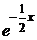 ,
,  =x·
=x·  = x·
= x· 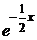 .
.
4) Имея ФСР, запишем общее решение дифференциального уравнения  =
=  ·
·  +
+ 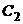 ·
·  =
=  ·
· 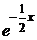 +
+ 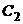 ·
· 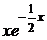 .
.
5) Найдем 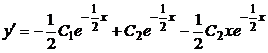 .
.
6) Из системы 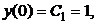
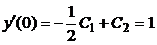 , находим
, находим 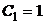 ,
, 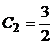 .
.
6) Записываем частное решение 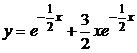 , удовлетворяющее начальным условиям.
, удовлетворяющее начальным условиям.
Ответ. Общее решение  =
=  ·
· 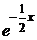 +
+ 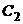 ·
· 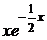 , частное решение
, частное решение 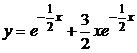 .
.
Задание 2.1. Решить задачу Коши для уравнений.
| Вар. | Уравнение | Начальные условия |
| 2.1.1 | 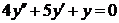 ; ;
|  . .
|
| 2.1.2. | 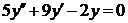 ; ;
|  . .
|
| 2.1.3. | 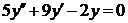 ; ;
|  . .
|
| 2.1.4. |  ; ;
|  . .
|
| 2.1.5. | 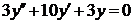 ; ;
|  . .
|
| 2.1.6. | 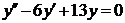 ; ;
|  . .
|
| 2.1.7. | 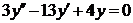 ; ;
|  . .
|
| 2.1.8. | 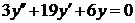 ; ;
|  . .
|
| 2.1.9. | 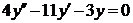 ; ;
|  . .
|
| 2.1.10. | 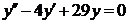 ; ;
| 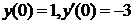 . .
|
| 2.1.11. | 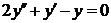 ; ;
|  . .
|
| 2.1.12. | 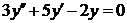 ; ;
|  . .
|
| 2.1.13. | 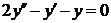 ; ;
| 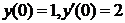 . .
|
| 2.1.14. | 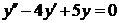 ; ;
| 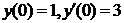 . .
|
| 2.1.15. | 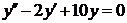 ; ;
| 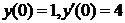 . .
|
| 2.1.16. | 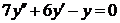 ; ;
|  . .
|
| 2.1.17. | 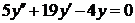 ; ;
|  . .
|
| 2.1.18. | 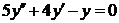 ; ;
|  . .
|
| 2.1.19. | 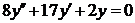 ; ;
|  . .
|
| 2.1.20. | 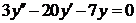 ; ;
|  . .
|
| 2.1.21. | 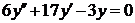 ; ;
|  . .
|
| 2.1.22. | 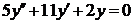 ; ;
|  . .
|
| 2.1.23. | 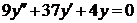 ; ;
|  . .
|
| 2.1.24. | 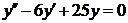 ; ;
| 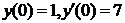 . .
|
| 2.1.25. | 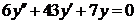 ; ;
|  . .
|
| 2.1.26. | 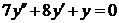 ; ;
|  . .
|
| 2.1.27. | 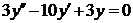 ; ;
|  . .
|
| 2.1.28. | 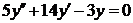 ; ;
|  . .
|
| 2.1.29. | 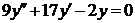 ; ;
|  . .
|
| 2.1.30. |  ; ;
|  . .
|
2.2. Линейные однородные дифференциальные уравнения n-го порядка
|
|
|
Для решения однородных дифференциальных уравнений с постоянными коэффициентами
n-гопорядка 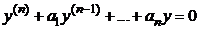 применяют описанный в п.2.1. алгоритм решения уравнений 2-го порядка, то есть записывают характеристическое уравнение
применяют описанный в п.2.1. алгоритм решения уравнений 2-го порядка, то есть записывают характеристическое уравнение 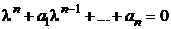 и находят его корни. Необходимо лишь учесть, что:
и находят его корни. Необходимо лишь учесть, что:
1) каждому действительному корню 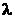 кратности
кратности  характеристического уравнения соответствует
характеристического уравнения соответствует  решений в ФСР:
решений в ФСР: 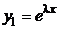 и
и 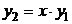 , …,
, …, 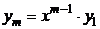 ;
;
2) каждой паре комплексных корней  кратности
кратности  характеристического уравнения соответствует
характеристического уравнения соответствует 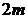 решений в ФСР:
решений в ФСР: 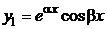 ,
,  ,
, 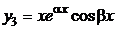 ,
, 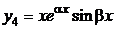 ,…,
,…, 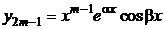 ,
, 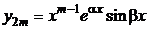 .
.
Задание 2.2. Найти общие решения уравнений.
| Вар. | Уравнение | Вар. | Уравнение |
| 2.2.1. | 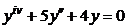 . .
| 2.2.16. | 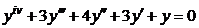 . .
|
| 2.2.2. | 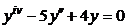 . .
| 2.2.17. | 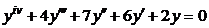 . .
|
| 2.2.3. | 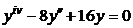 . .
| 2.2.18. | 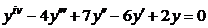 . .
|
| 2.2.4. |  . .
| 2.2.19. |  . .
|
| 2.2.5. | 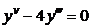 . .
| 2.2.20. | 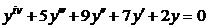 . .
|
| 2.2.6. | 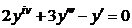 . .
| 2.2.21. | 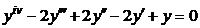 . .
|
| 2.2.7. | 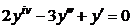 . .
| 2.2.22. | 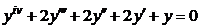 . .
|
| 2.2.8. | 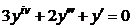 . .
| 2.2.23. | 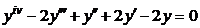 . .
|
| 2.2.9. | 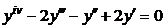 . .
| 2.2.24. | 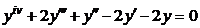 . .
|
| 2.2.10. | 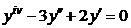 . .
| 2.2.25. | 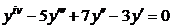 . .
|
| 2.2.11. | 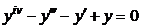 . .
| 2.2.26. | 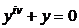 . .
|
| 2.2.12. | 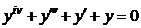 . .
| 2.2.27. | 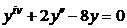 . .
|
| 2.2.13. | 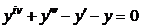 . .
| 2.2.28. |  . .
|
| 2.2.14. | 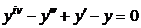 . .
| 2.2.29. | 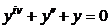 . .
|
| 2.2.15. | 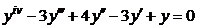 . .
| 2.2.30. | 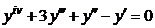 . .
|
Метод вариации произвольных постоянных решения неоднородных дифференциальных уравнений
|
|
|
Для решения линейных неоднородных дифференциальных уравнений может быть использован метод вариации произвольных постоянных. Опишем его алгоритм на примере неоднородного дифференциального уравнения с постоянными коэффициентами 2-го порядка.
1) Для заданного уравнения 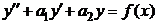 запишем соответствующее ему однородное дифференциальное уравнение
запишем соответствующее ему однородное дифференциальное уравнение
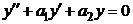 . (2.1)
. (2.1)
2) Находим общее решение данного однородного уравнения: 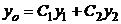 , где
, где  и
и 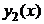 – функции ФСР, а
– функции ФСР, а  и
и 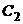 – произвольные постоянные.
– произвольные постоянные.
3) Заменим постоянные  и
и 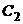 на функции
на функции 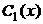 и
и 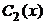 , причём так, что функция
, причём так, что функция 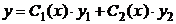 будет уже решением неоднородного уравнения.
будет уже решением неоднородного уравнения.
4) Найдём производную 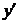 для функции
для функции 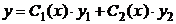 :
: 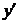 =
= 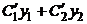 +
+ 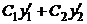 и потребуем
и потребуем
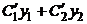 =0, (2.2)
=0, (2.2)
то есть, чтобы производная 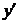 имела такой же вид, как и при постоянных
имела такой же вид, как и при постоянных  и
и 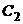 .
.
|
|
|
5) Учитывая (2.2), найдём производную 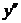 . Получаем
. Получаем 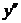 =
= 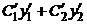 +
+ 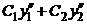 .
.
6) Подставив  ,
, 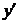 и
и 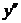 в исходное уравнение и учитывая, что
в исходное уравнение и учитывая, что  и
и 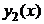 являются решениями однородного уравнения, получаем ещё одно требование к функциям
являются решениями однородного уравнения, получаем ещё одно требование к функциям 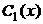 и
и 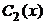
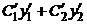 =
= 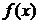 . (2.3)
. (2.3)
7) Из условий (2.2) и (2.3) составляем систему:
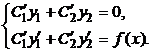 (2.4)
(2.4)
8) Из системы (2.4) нетрудно получить выражения: 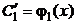 и
и 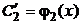 , которые затем интегрируем:
, которые затем интегрируем:
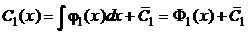 и
и 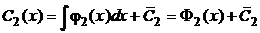 . (2.5)
. (2.5)
В выражении (2.5) величины 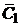 и
и 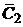 – произвольные постоянные.
– произвольные постоянные.
9) Используя (2.5), то есть выражения для функций 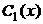 и
и 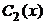 , записываем общее решение неоднородного уравнения:
, записываем общее решение неоднородного уравнения:
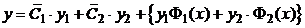 . (2.6)
. (2.6)
Из (2.6) следует, что общее решение неоднородного уравнения представляется в виде 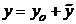 , где
, где 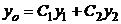 – общее решение однородного уравнения (2.1), а функция
– общее решение однородного уравнения (2.1), а функция  =
= 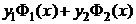 – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
Пример 2.3. Решить задачу Коши  ,
, 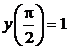 ,
, 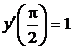 , применив метод вариации произвольных постоянных.
, применив метод вариации произвольных постоянных.
Решение: 1) Составляем характеристическое уравнение 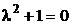 .
.
2) Характеристические корни уравнения:  . ФСР:
. ФСР: 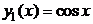 и
и 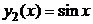 . Составим общее решение однородного уравнения:
. Составим общее решение однородного уравнения:  =
= 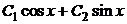 .
.
3) Составим систему: 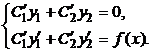 В нашем случае:
В нашем случае: 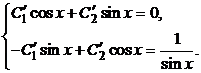 Из этой системы получаем
Из этой системы получаем  и
и 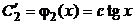 .
.
4) Вычислим: 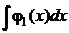 =
= 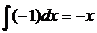 и
и 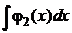 =
= 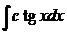 =
= 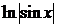 . Составим частное решение неоднородного уравнения
. Составим частное решение неоднородного уравнения
 =
= 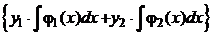 =
= 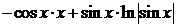 .
.
5) Составим общее решение неоднородного уравнения 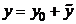 .
.
6) Для заданных начальных условий получаем 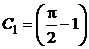 ,
,  .
.
Ответ: Общее решение: 
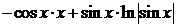 , частное решение:
, частное решение: 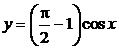
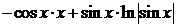 .
.
Задание 2.3. Решить задачу Коши, применяя метод вариации произвольных постоянных.
| Вар. | Уравнение | Начальные условия |
| 2.3.1 | 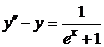 ; ;
| 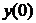 =1, =1, 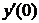 = = 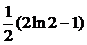 . .
|
| 2.3.2. | 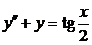 ; ;
| 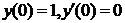 . .
|
| 2.3.3. | 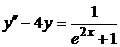 ; ;
| 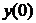 =1, =1, 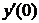 = = 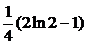 . .
|
| 2.3.4. | 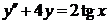 ; ;
|  . .
|
| 2.3.5. | 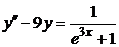 ; ;
| 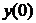 =1, =1, 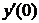 = = 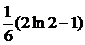 . .
|
| 2.3.6. | 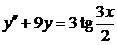 ; ;
| 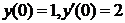 . .
|
| 2.3.7. | 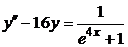 ; ;
| 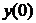 =1, =1, 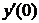 = = 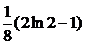 . .
|
| 2.3.8. | 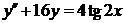 ; ;
| 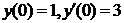 . .
|
| 2.3.9. |  ; ;
| 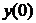 =1, =1, 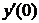 = = 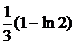 . .
|
| 2.3.10. | 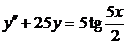 ; ;
| 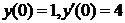 . .
|
| 2.3.11. | 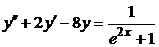 ; ;
| 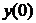 =1, =1, 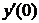 = = 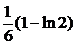 . .
|
| 2.3.12. | 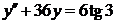 ; ;
| 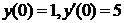 . .
|
| 2.3.13. | 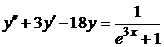 ; ;
| 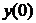 =1, =1, 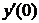 = = 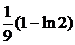 . .
|
| 2.3.14. | 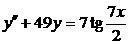 ; ;
| 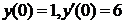 . .
|
| 2.3.15. | 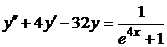 ; ;
| 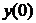 =1, =1, 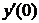 = = 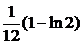 . .
|
| 2.3.16. | 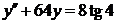 ; ;
| 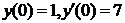 . .
|
| 2.3.17. | 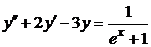 ; ;
| 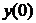 =1, =1, 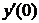 = = 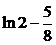 . .
|
| 2.3.18. | 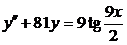 ; ;
| 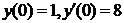 . .
|
| 2.3.19. | 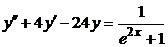 ; ;
| 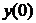 =1, =1, 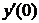 = = 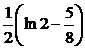 . .
|
| 2.3.20. | 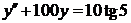 ; ;
| 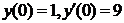 . .
|
| 2.3.21. | 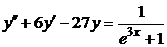 ; ;
| 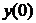 =1, =1, 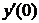 = = 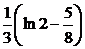 . .
|
| 2.3.22. | 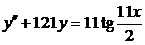 ; ;
| 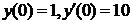 . .
|
| 2.3.23. | 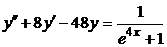 ; ;
| 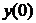 =1, =1, 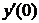 = = 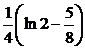 . .
|
| 2.3.24. |  ; ;
| 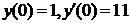 . .
|
| 2.3.25. |  ; ;
| 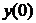 =1, =1, 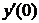 = = 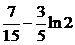 . .
|
| 2.3.26. | 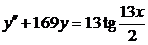 ; ;
| 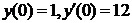 . .
|
| 2.3.27. | 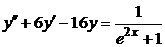 ; ;
| 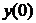 =1, =1, 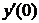 = = 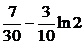 . .
|
| 2.3.28. | 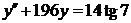 ; ;
| 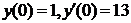 . .
|
| 2.3.29. | 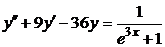 ; ;
| 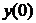 =1, =1, 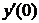 = = 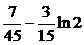 . .
|
| 2.3.30. | 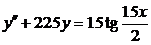 ; ;
| 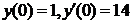 . .
|
2.4. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида 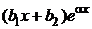
Общее решение линейного неоднородного дифференциального уравнения 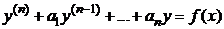 может быть записано в виде
может быть записано в виде  , где
, где 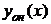 – общее решение неоднородного уравнения,
– общее решение неоднородного уравнения, 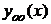 – общее решение соответствующего однородного уравнения,
– общее решение соответствующего однородного уравнения, 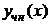 – частное решение неоднородного уравнения. Если правая часть неоднородного уравнения имеет некоторый специальный вид, то частное решение можно найти методом неопределенных коэффициентов.
– частное решение неоднородного уравнения. Если правая часть неоднородного уравнения имеет некоторый специальный вид, то частное решение можно найти методом неопределенных коэффициентов.
В данном пункте рассмотрим метод для уравнения 2-го порядка 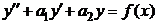 с постоянными коэффициентами и правой частью вида
с постоянными коэффициентами и правой частью вида  , где
, где 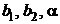 – действительные числа.
– действительные числа.
Общий алгоритм решения со специальной правой частью указанного вида следующий:
1) Находим корни  характеристического уравнения
характеристического уравнения 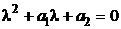 .
.
2) Если ни один из корней  не совпадает с
не совпадает с  (нерезонансный случай), то частное решение ищем в виде
(нерезонансный случай), то частное решение ищем в виде 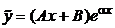 , где
, где 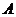 и
и 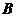 – неопределённые коэффициенты, подлежащие вычислению;
– неопределённые коэффициенты, подлежащие вычислению;
3) Так как функция  должна быть решением заданного неоднородного уравнения, то вычислив
должна быть решением заданного неоднородного уравнения, то вычислив  ,
,  и подставив функцию
и подставив функцию  и её производные в заданное уравнение, получаем тождество, из которого находим значения коэффициентов
и её производные в заданное уравнение, получаем тождество, из которого находим значения коэффициентов 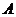 и
и 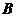 .
.
4) Если (случай резонанса):
4.1) 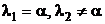 , то частное решение ищем в виде
, то частное решение ищем в виде 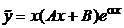 .
.
4.2) 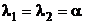 , то решение частное решение ищем в виде
, то решение частное решение ищем в виде 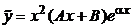 .
.
Если 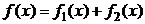 , где каждая из функций
, где каждая из функций  имеет указанный выше вид, то частное решение находят как сумму соответствующих частных решений
имеет указанный выше вид, то частное решение находят как сумму соответствующих частных решений  .
.
Пример 2.4. Решить уравнение: 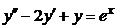 , применив метод неопределённых коэффициентов.
, применив метод неопределённых коэффициентов.
Решение: 1) Характеристические корни уравнения: 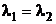 =1. Общее решение однородного уравнения, соответствующего заданному уравнению:
=1. Общее решение однородного уравнения, соответствующего заданному уравнению: 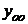 =
=  =
=  .
.
2) Так как 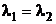
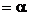 =
= 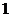 , частное решение
, частное решение  ищем в виде
ищем в виде 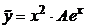 , где
, где 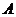 – неопределённый коэффициент.
– неопределённый коэффициент.
3) Находим производные:  =
=  ,
,  =
= 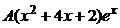 . Подставляя функцию
. Подставляя функцию  и её производные в заданное уравнение, получаем тождество
и её производные в заданное уравнение, получаем тождество  . Упрощая, получим равенство
. Упрощая, получим равенство 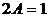 , из которого находим значение
, из которого находим значение 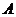 =
= 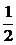 .
.
4) Записываем общее решение неоднородного уравнения 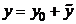 =
=  +
+ 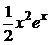 .
.
Ответ. Общее решение:  =
=  +
+ 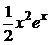 .
.
Пример 2.5. Решить уравнение: 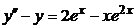 , применив метод неопределённых коэффициентов.
, применив метод неопределённых коэффициентов.
Решение: 1) Корни характеристического уравнения 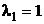
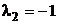 . Следовательно, общее решение соответствующего однородного уравнения
. Следовательно, общее решение соответствующего однородного уравнения 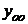 =
=  =
= 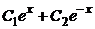 , где
, где  и
и 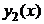 – функции фундаментальной системы решений, а
– функции фундаментальной системы решений, а  и
и 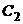 – произвольные постоянные.
– произвольные постоянные.
2) Так как 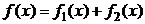 , необходимо найти частные решения:
, необходимо найти частные решения:
а) для правой части 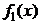 =
= 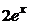 , при условии, что
, при условии, что 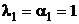 ищем
ищем 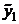 =
= 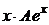 ;
;
б) для правой части 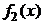 =
= 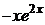 , при условии, что
, при условии, что 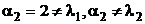 ищем
ищем 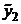 =
= 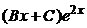 .
.
3) Подставляя функцию 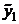 и её производные в уравнение с правой частью
и её производные в уравнение с правой частью 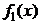 , получаем тождество, из которого находим значение
, получаем тождество, из которого находим значение 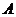 =1.
=1.
4) Подставляя функцию 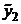 и её производные в заданное уравнение, получаем тождество, из которого находим
и её производные в заданное уравнение, получаем тождество, из которого находим 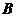 =
= 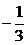 ,
, 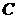 =
= 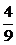 .
.
5) Учитывая  , запишем
, запишем  =
= 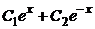
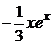 +
+ 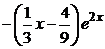 .
.
Ответ. Общее решение:  =
= 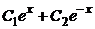
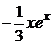 +
+ 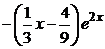 .
.
Задание 2.4. Решить уравнения, применяя метод неопределённых коэффициентов.
| Вар. | Уравнение | Вар. | Уравнение |
| 2.4.1. | 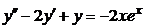 . .
| 2.4.16. |  . .
|
| 2.4.2. | 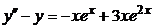 . .
| 2.4.17. | 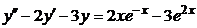 . .
|
| 2.4.3. | 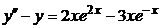 . .
| 2.4.18. | 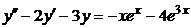 . .
|
| 2.4.4. | 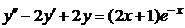 . .
| 2.4.19. | 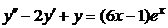 . .
|
| 2.4.5. | 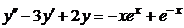 . .
| 2.4.20. |  . .
|
| 2.4.6. | 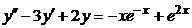 . .
| 2.4.21. | 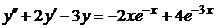 . .
|
| 2.4.7. | 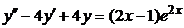 . .
| 2.4.22. | 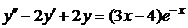 . .
|
| 2.4.8. | 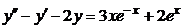 . .
| 2.4.23. | 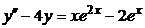 . .
|
| 2.4.9. | 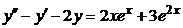 . .
| 2.4.24. | 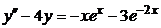 . .
|
| 2.4.10. | 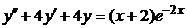 . .
| 2.4.25. |  . .
|
| 2.4.11. | 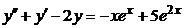 . .
| 2.4.26. | 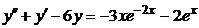 . .
|
| 2.4.12. | 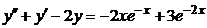 . .
| 2.4.27. | 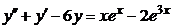 . .
|
| 2.4.13. | 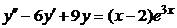 . .
| 2.4.28. | 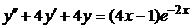 . .
|
| 2.4.14. |  . .
| 2.4.29. |  . .
|
| 2.4.15. | 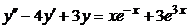 . .
| 2.4.30. |  . .
|
2.5. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида 
Алгоритм решения неоднородных дифференциальных уравнений 2-го порядка с правой частью вида  такой же, как и для правой части вида неоднородных дифференциальных уравнений 2-го порядка с правой частью вида
такой же, как и для правой части вида неоднородных дифференциальных уравнений 2-го порядка с правой частью вида  :
:
1) частное решение неоднородного уравнения ищем в виде  =
= 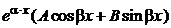 , если ни один из корней характеристического уравнения не совпадает с числом
, если ни один из корней характеристического уравнения не совпадает с числом 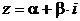 , построенном по виду правой части неоднородного уравнения (нерезонансный случай);
, построенном по виду правой части неоднородного уравнения (нерезонансный случай);
2) если характеристическое уравнение имеет комплексно сопряженные корни и один из них совпадает с числом 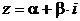 , то имеем резонансный случай и частное решение ищем в виде
, то имеем резонансный случай и частное решение ищем в виде  =
= 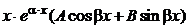 .
.
Значения «неопределённых коэффициентов» 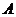 и
и 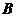 вычисляем способом, изложенным в п.2.4 и ниже в примерах.
вычисляем способом, изложенным в п.2.4 и ниже в примерах.
Пример 2.6. Решить уравнение: 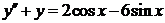 , применив метод неопределённых коэффициентов.
, применив метод неопределённых коэффициентов.
Решение. 1) Характеристическое уравнение имеет комплексно сопряженные корни  =
= 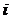 ,
,  =
= 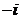 . Общее решение однородного уравнения
. Общее решение однородного уравнения 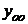 =
=  =
= 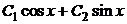 .
.
2) Запишем правую часть 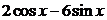 исходного уравнения в виде
исходного уравнения в виде 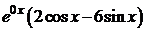 . Ей соответствует число
. Ей соответствует число  . Так как
. Так как 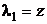 , то имеем резонансный случай и частное решение
, то имеем резонансный случай и частное решение  ищем в виде
ищем в виде  =
= 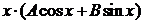 .
.
3) Найдем производные  =
= 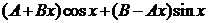 ,
,  =
= 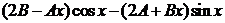 . Подставляя функцию
. Подставляя функцию  и её производные в заданное уравнение, получаем тождество, из которого находим значения
и её производные в заданное уравнение, получаем тождество, из которого находим значения 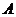 =3,
=3, 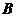 =1. Это значит, что
=1. Это значит, что  =
= 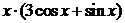 .
.
4) Составим общее решение неоднородного уравнения 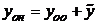 .
.
Ответ. Общее решение  =
= 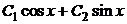 +
+ 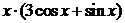 .
.
Пример 2.7. Решить уравнение 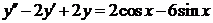 , применив «метод неопределённых коэффициентов».
, применив «метод неопределённых коэффициентов».
Решение. 1) Характеристические корни уравнения  =
= 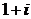 ,
,  =
=  . Общее решение соответствующего однородного уравнения
. Общее решение соответствующего однородного уравнения 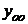 =
=  =
= 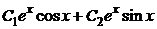 .
.
2) Так как 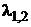 =
= 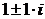
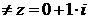 , частное решение
, частное решение  ищем в виде
ищем в виде  =
= 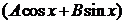 , где
, где 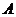 и
и 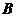 подлежат вычислению.
подлежат вычислению.
3) Найдем производные  =
= 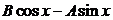 ,
,  =
= 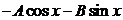 . Подставляя функцию
. Подставляя функцию  и её производные в заданное уравнение, получаем тождество, из которого находим значения
и её производные в заданное уравнение, получаем тождество, из которого находим значения 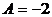 ,
, 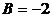 . Это значит, что
. Это значит, что  =
= 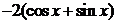
4) Составим общее решение неоднородного уравнения  .
.
Ответ. Общее решение: 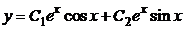
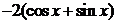 .
.
Задание 2.5. Решить уравнения, применяя метод неопределённых коэффициентов.
| Вар. | Уравнение | Вар. | Уравнение: |
| 2.5.1. |  . .
| 2.5.16. | 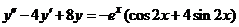 . .
|
| 2.5.2. | 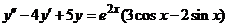 . .
| 2.5.17. | 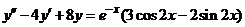 . .
|
| 2.5.3. | 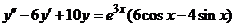 . .
| 2.5.18. | 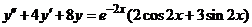 . .
|
| 2.5.4. | 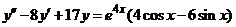 . .
| 2.5.19. | 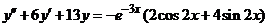 . .
|
| 2.5.5. | 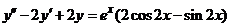 . .
| 2.5.20. | 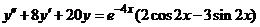 . .
|
| 2.5.6. | 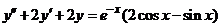 . .
| 2.5.21. | 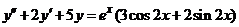 . .
|
| 2.5.7. | 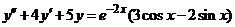 . .
| 2.5.22. | 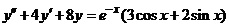 . .
|
| 2.5.8. | 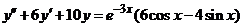 . .
| 2.5.23. | 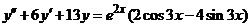 . .
|
| 2.5.9. | 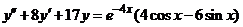 . .
| 2.5.24. | 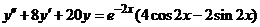 . .
|
| 2.5.10. | 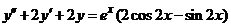 . .
| 2.5.25. | 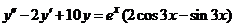 . .
|
| 2.5.11. | 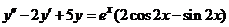 . .
| 2.5.26. |  . .
|
| 2.5.12. | 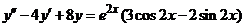 . .
| 2.5.27. | 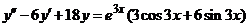 . .
|
| 2.5.13. | 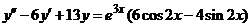 . .
| 2.5.28. | 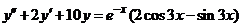 . .
|
| 2.5.14. | 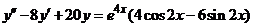 . .
| 2.5.29. | 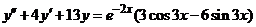 . .
|
| 2.5.15. |  . .
| 2.5.30. |  . .
|
2.6. Линейные неоднородные дифференциальные уравнения 3-го и 4-го
порядков со специальной правой частью
Алгоритм нахождения частного решения неоднородных дифференциальных уравнений n-го порядка со специальной правой частью такой же, как и для неоднородных уравнений 2-го порядка. Отличие состоит лишь в том, что значение показателя  в множителе
в множителе 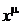 в резонансном случае может быть больше 1.
в резонансном случае может быть больше 1.
Пример 2.8. Записать вид частного решения для уравнения: 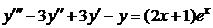 .
.
Решение. 1) Находим корни характеристического уравнения: 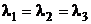 =1, то есть число 1 является корнем кратности 3.
=1, то есть число 1 является корнем кратности 3.
2) По виду правой части 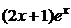 записываем число
записываем число 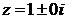 .
.
3) Так как 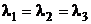 =
= 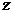 , частное решение
, частное решение  ищем в виде
ищем в виде 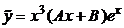 , где
, где 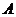 и
и 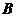 – неопределённые коэффициенты.
– неопределённые коэффициенты.
Ответ. Частное решение ищем в виде 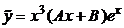 (резонансный случай).
(резонансный случай).
Пример 2.9. Записать вид частного решения для уравнения 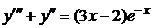 .
.
Решение. 1) Характеристические корни 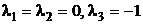 .
.
2) По виду правой части 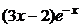 записываем число
записываем число 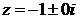 .
.
3) Так как с числом 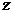 совпадает лишь корень
совпадает лишь корень 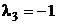 кратности 1, то частное решение ищем в виде
кратности 1, то частное решение ищем в виде 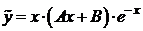 (резонансный случай).
(резонансный случай).
Ответ. Частное решение ищем в виде 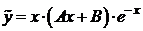 .
.
Пример 2.10. Записать вид частного решения для уравнения  .
.
Решение: 1) Характеристические корни уравнения  =
=  ,
,  =
= 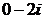 ,
, 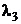 =2.
=2.
2) По виду правой части  записываем число
записываем число  .
.
3) Так как  =
= 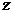 , частное решение
, частное решение  ищем в виде
ищем в виде  =
= 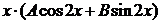 (резонансный случай).
(резонансный случай).
Ответ. Частное решение ищем в виде  =
= 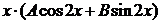 .
.
Пример 2.11. Записать вид частного решения для уравнения 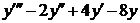 =
= 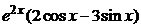 .
.
Решение. 1) Корни характеристического уравнения  =2,
=2,  =
= 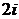
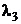 =
= 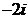 .
.
2) По виду правой части 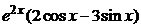 записываем число
записываем число 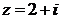 .
.
3) Так как комплексное число 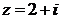 не совпадает ни с
не совпадает ни с  =2, ни с
=2, ни с  =
= 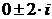 , то частное решение уравнения следует искать в виде
, то частное решение уравнения следует искать в виде  =
= 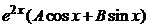 (нерезонансный случай).
(нерезонансный случай).
Ответ. Частное решение ищем в виде  =
= 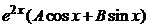 .
.
Дата добавления: 2018-02-15; просмотров: 3281; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
