Движение тела, брошенного под углом к горизонту
Пусть тело брошено под углом α к горизонту со скоростью  . Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — ОхиОу (рис. 8.1).
. Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — ОхиОу (рис. 8.1).
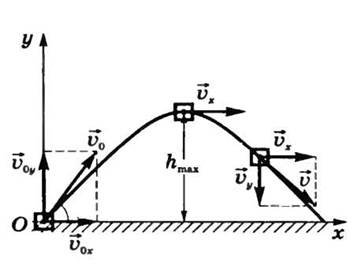
Рисунок 8.1. Движение тела, брошенного под углом к горизонту.
Начало отсчета совместим с начальным положением тела. Проекции начальной скорости на осиОу и Ох:
 ,
,
 .
.
Проекции ускорения:
 ,
, 
Тогда движение тела будет описываться уравнениями:
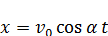 (8.1)
(8.1)
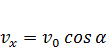 (8.2)
(8.2)
 (8.3)
(8.3)
 (8.4)
(8.4)
Из этих формул следует, что в горизонтальном направлении тело движется равномерно, а в вертикальном — равноускоренно.
Траекторией движения тела будет парабола. Учитывая, что в верхней точке параболы  , можно найти время подъема тела до верхней точки параболы:
, можно найти время подъема тела до верхней точки параболы:
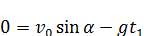
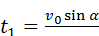 (8.5)
(8.5)
Подставив значение t1 в уравнение (8.3), найдем максимальную высоту подъема тела:
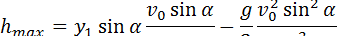
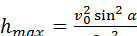 — максимальная высота подъема тела.
— максимальная высота подъема тела.
Время полета тела находим из условия, что приt=t2 координата у2=0. Следовательно,
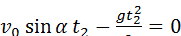 .
.
|
|
|
Отсюда,
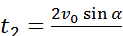 — времяполета тела.
— времяполета тела.
Сравнивая эту формулу с формулой (8.5), видим, чтоt2=2t1.
Время движения тела с максимальной высоты t3=t2-t1=2t1-t1=t1. Следовательно, сколько времени тело поднимается на максимальную высоту, столько времени оно опускается с этой высоты. Подставляя в уравнение координаты х (8.1) значение времени t2, найдем:
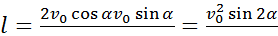 — дальность полета тела.
— дальность полета тела.
Мгновенная скорость в любой точке траектории направлена по касательной к траектории (см. рис. 8.1), модуль скорости определяется по формуле

Таким образом, движение тела, брошенного под углом к горизонту или в горизонтальном направлении, можно рассматривать как результат двух независимых движений — горизонтального равномерного и вертикального равноускоренного (свободного падения без начальной скорости или движения тела, брошенного вертикально вверх).
9. Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.
Положение тела на окружности определяется радиус-вектором  , проведенным из центра окружности. Модуль радиус-вектора равен радиусу окружностиR (рис. 9.1).
, проведенным из центра окружности. Модуль радиус-вектора равен радиусу окружностиR (рис. 9.1).
|
|
|
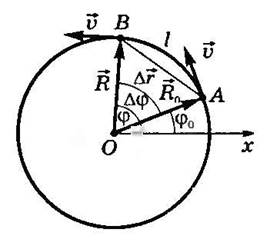
Рисунок 9.1. Движение тела по окружности.
За время Δt тело, двигаясь из точки А в точку В, совершает перемещение 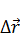 , равное хорде АВ, и проходит путь, равный длине дуги l.
, равное хорде АВ, и проходит путь, равный длине дуги l.
Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.
Скорость 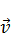 движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt, за который эта дуга пройдена:
движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt, за который эта дуга пройдена:
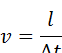
Скалярная физическая величина, численно равная отношению угла поворота радиус-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:

В СИ единицей угловой скорости является радиан в секунду  .
.
При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω=const; v=const.
Положение тела можно определить, если известен модуль радиус-вектора  и угол φ, который он составляет с осью Ох (угловая координата). Если в начальный момент времениt0=0 угловая координата равна φ0, ав момент времени t она равна φ, то угол поворота Δφрадиус-вектора за время Δt=t-t0 равен Δφ=φ-φ0. Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:
и угол φ, который он составляет с осью Ох (угловая координата). Если в начальный момент времениt0=0 угловая координата равна φ0, ав момент времени t она равна φ, то угол поворота Δφрадиус-вектора за время Δt=t-t0 равен Δφ=φ-φ0. Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:
|
|
|
φ=φ0+ωt
Оно позволяет определить положение тела в любой момент времени t.
Учитывая, что 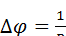 , получаем:
, получаем:

 — формула связи между линейнойи угловой скоростью.
— формула связи между линейнойи угловой скоростью.
Промежуток времени Т, в течение которого тело совершает один полный оборот, называется периодом вращения:
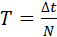 ,
,
Где N – число оборотов, совершенных телом за время Δt.
За время Δt=Т тело проходит путь l =2πR. Следовательно,

Величинаυ, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:
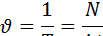
Следовательно,
 .
.
10. Ускорение при движении тела по окружности с постоянной по модулю скоростью (центростремительное ускорение)
При равномерном вращении по окружности модуль скорости движения тела не изменяется, но направление скорости изменяется непрерывно. Следовательно, данное движение — движение с ускорением. Оно характеризует быстроту изменения скорости по направлению.
По определению среднего ускорения
 .
.
Треугольники ОАВ иВСD — равнобедренные (рис. 10.1).
|
|
|
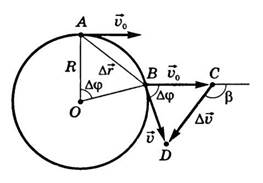
Рисунок 10.1. Скорость при движении по окружности
Углы при вершинах — одинаковые (как углы с соответственно перпендикулярными сторонами). Отсюда следует, чтоΔОАВ подобенΔВСD.
Из подобия

Тогда
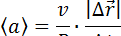
Мгновенное ускорение
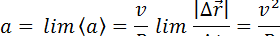
β — угол между 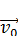 и
и 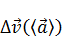 —внешний по отношению к ΔВСD:
—внешний по отношению к ΔВСD:
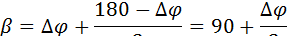
При Δt→0 угол Δφ→0 и, следовательно, β→90°. Перпендикуляром к касательной к окружности является радиус. Следовательно, 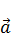 направлено по радиусу к центру и поэтому называется центростремительным ускорением:
направлено по радиусу к центру и поэтому называется центростремительным ускорением:

Модуль  , направление
, направление 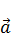 непрерывно изменяется (рис. 10.2). Поэтому данное движение не является равноускоренным.
непрерывно изменяется (рис. 10.2). Поэтому данное движение не является равноускоренным.

Рисунок 10.2. Центростремительное ускорение
Дата добавления: 2021-03-18; просмотров: 140; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
