ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТА
ИНЕРЦИИ МАХОВИКА И СИЛЫ ТРЕНИЯ В ОПОРЕ
Для определения этих величин воспользуемся законом сохранения механической энергии для системы в которой действует сила трения.
Под действием силы тяжести груз массой M начинает опускаться, раскручивая маховик с валом . Если в результате движения до полного разматывания шнура груз проходит расстояние h1 , то первоначальный запас энергии был равен потенциальной энергии груза в поле земного тяготения Ep = Mgh 1 .
По мере опускания груза, этот запас энергии переходит в кинетическую энергию поступательного движения груза 
, кинетическую энергию вращения 
и энергию (работу), расходуемую на преодоление силы трения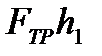 
. Поэтому, в момент нахождения груза в нижней точке, закон сохранения энергии будет иметь вид:
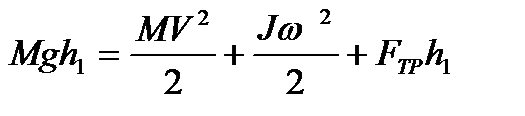(5)
Вращаясь далее по инерции, маховик начнет наматывать шнур и поднимать груз. Подъем будет продолжаться до тех пор, пока часть энергии, равная полной кинетической энергии маховика в нижней точке 
, не перейдет в потенциальную энергию груза 
, поднятого на новую высоту, а оставшаяся часть ее, не будет израсходована на преодоление силы трения при подъеме, т.е. на работу 
. Следовательно на высоте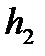 
, закон сохранения энергии для данной системы можно записать в виде:
(6)
|
|
|
Из (5) и (6) получаем, что убыль потенциальной энергии груза равна работе на преодоление сил трения:
(7)
Откуда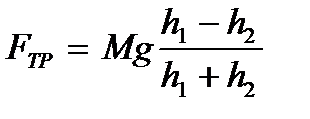 
(8)
Эта формула позволяет определить силу трения в опоре, если известна масса ,
начальное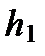 
и конечное 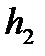положения груза.
Так как груз при опускании движется равноускоренно, то скорость груза в нижней точке V=at, , где a и t ускорение и время опускания груза. Угловая скорость вращения маховика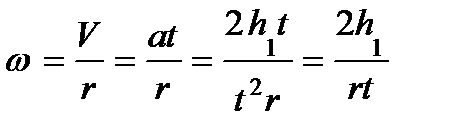 
, где r радиус шкива на который наматывается шнур. Из уравнения (5)
. (9)
Подставляя значения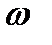 
, V и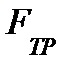 
, после преобразований получаем формулу для косвенного измерения момента инерции по результатам прямых измерений величин 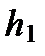, , 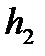r и t :
(10)
5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
5.1. Медленно разматывая шнур, опустите груз до нижней точки и снимите отсчет его положения по линейной шкале.
5.2. Наматывая шнур на шкив, поднимите груз до максимально возможного деления линейной шкалы. Снимите отсчет.
|
|
|
5.3. Определите высоту 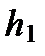как разность полученных отсчетов. Это будет высота,
соответствующая исходному значению полной энергии груза.
5.4. Включите секундомер и одновременно отпустите груз. Определите время его движения до нижней точки.
5.5. Не останавливая движения груза по инерции, снимите отсчет по шкале в момент остановки груза в верхней точке.
5.6. Определите высоту 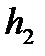на которую поднимется груз.
5.7. Повторите измерения три раза и найдите средние значения t, 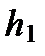и .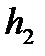
5.8. По формуле (10) определите измеренное косвенным методом среднее значение момента инерции маховика с валом.
5.9. По формуле (8) определите измеренное косвенным методом среднее значение величины силы трения .
5.10. По формуле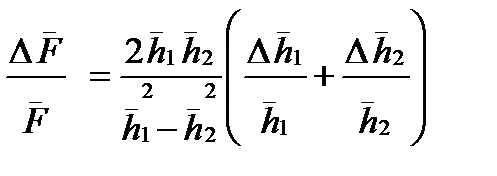 
рассчитайте среднюю абсолютную ошибку измерения величины силы трения.
5.11. Результат измерения силы трения представьте в виде 
6. ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
6.1. При помощи штангенциркуля измерьте геометрические размеры маховика и вала, указанные на рис. 2 и занесите их в таблицу 2.
Таблица 2
| Установка № | 
| 
| 
| 
| 
| 
| 
| 
| 
|
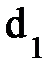
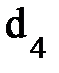
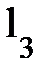
Длина вала L в установке 1 равна 290 мм, в установке 2 - 250 мм.
|
|
|
6.2. По формуле (4) получите рассчетное значение величины момента инерции.
6.3. Сравните результаты измерений (п.5.8) и результаты расчета (п.6.2) момента инерции.
7. КОНТРОЛЬНЫЕ ВОПРОСЫ
7.1. Что называется моментом инерции и в каких единицах он измеряется?
7.2. В чем смысл аддитивности момента инерции?
7.3. Какие величины необходимо знать для определения момента инерции
маховика с валом:
а) расчетным путем?
б) путем косвенных измерений?
7.4. Сформулируйте закон сохранения энергии для систем в которых одновременно действуют консервативные и внешние силы?
7.5. Объясните как получена формула для определения абсолютной
погрешности измерения величины силы трения.
ЛАБОРАТОРНАЯ РАБОТА №7
ИЗУЧЕНИЕ ОСНОВНОГО ЗАКОНА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
Цель работы. Экспериментальная проверка второго закона Ньютона для вращательного движения.
Приборы и принадлежности:
1. Маятник Обербека,
|
|
|
2. Секундомер.
3. Линейка.
4. Штангенциркуль.
5. Весы.
1. Теоретическое введение
Рассмотрим основной закон динамики вращательного движения на примере тела, вращающегося с угловой скоростью ω вокруг оси 001.
Выберем произвольно некоторую точку массой mi на расстоянии ri от оси вращения. Все внутренние силы, действующие на эту точку обозначим Fi вн и спроектируем их на прямую, перпендикулярную радиусу ri и находящуюся в плоскости перпендикулярной оси 001. Проекцию всех внешних сил на эту же прямую обозначим Fi вш.
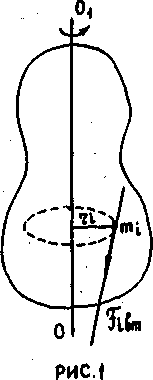Тогда в соответствии со вторым законом Ньютона для i -ой точки можно записать
mi а i = Fi вн + Fi вш, (1)
где а i - линейное ускорение. Учитывая, что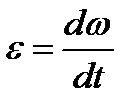 
, запишем для а i
. (2)
Подставляя (2) в (1) и умножая правую и левую части полученного уравнения на ri, получим
(3)
Просуммируем (3) по всем точкам твердого тела из которых оно состоит
. (4)
Так как внутренние силы не могут вызвать вращения тела вокруг оси, то их суммарный момент равен нулю
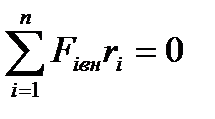(5)
и уравнение (4) упростится
(6)
Величина, определяемая произведением массы точки на квадрат расстояния до оси вращения, называется ее моментом инерции. Просуммировав моменты инерции всех точек твердого тела, получаем момент инерции всего тела
(7)
Сумма в правой части формулы (6) представляет собой результирующий или главный момент внешних сил
(8)
Учитывая, что ускорение тела 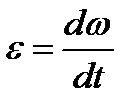, из формулы (6) получим ε = M / J
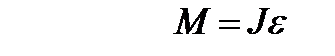(9)
Это и есть основной закон динамики вращательного движения, который является фактически вторым законом динамики Ньютона, записанным для вращательного движения. В такой записи этот закон еще называют уравнением движения вращающегося тела.
При вращательном движении твердого тела результирующий момент внешних сил равен произведению момента инерции тела на угловое ускорение.
В данной работе для проверки справедливости этого закона нужно убедиться, что
1) при постоянном моменте инерции отношение угловых ускорений прямо пропорционально отношению главных моментов внешних сил, вызывающих эти ускорения, т.е. ε1/ε2= M1/M2;
2) при постоянном вращающем моменте силы отношение угловых ускорений обратно пропорционально моментам инерции, которым они соответствуют, т.е. ε2/ ε1= J1/J2
Основной закон динамики вращательного движения проверяется на устройстве, называемом маятником Обербека (рис. 2). Установка состоит из крестовины, на которой закрепляется грузы равные по массе m 1= m 2= m 3= m 4. На оси имеется двухступенчатый шкив с диаметрами D 1 и D 2. Нить с приводным грузом m закрепляется на шпильке шкива для исключения проскальзывания и наматывается на него, поднимая за собой груз на заданную высоту. При опускания груза под действием силы тяжести механическая система приходит во вращательное движение под действием момента силы
M = T ( D /2) , (10)
величина которого определяется силой натяжения нити T и расстоянием от оси вращения до точки приложения силы натяжения, т.е. радиусом используемого шкива. Сила натяжения определяется из уравнения поступательного движения приводного груза массы m (второго закона Ньютона для поступательного движения) и равна
T = m ( g – a ), (11)
T – сила натяжения нити; а – линейное ускорение груза; g – ускорение свободного падения.
Подставляя эту силу натяжения в (10) получаем
(12)
Линейное ускорение a определяется по времени перемещения груза m на расстояние h по вертикали. Оно определяется в соответствии с законом движения при постоянном ускорении
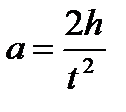(13)
С другой стороны, оно однозначно связано с угловым ускорением ε поскольку нить нерастяжима и все ее точки движутся с одинаковым линейным ускорением a
(14)
2. Порядок выполнения работы
Первая часть: Момент инерции маятника постоянен (грузы закреплены например на концах крестовины и их положение остается неизменным в процессе измерений). Момент силы M изменяется при изменении точки приложения силы натяжения нити T, т.е. при поочередном использовании большего и меньшего шкивов. Угловые ускорения при этом должны меняться пропорционально вращающему моменту сил ε1/ε2=M1/M2.
2.1. Взвесьте приводной груз m и занесите результаты в табл. 1.
2.2. Закрепите подвижные грузы на концах (или середине), проверьте находится ли маятник в безразличном равновесии.
2.3. Намотайте нить сначала на малый шкив. Отпустите груз, одновременно включите секундомер и измерьте время опускания груза до подставки. Опыт повторите 3 раза с малым шкивом, потом 3 раза с большим. Положение грузов при этом не меняйте.
2.4. Измерьте штангенциркулем диаметры малого D 1 и большого D 2 шкива.
2.5. Произведите вычисления и убедитесь, что отношение моментов сил для разных шкивов равны отношению соответствующих угловых ускорений.
Результаты всех измерений занесите в таблицу.
Таблица 1
| Шкив меньшего диаметра D1 | N | m, кг | D , м | h, м | t, c | а, м/с2 | ε,с-2 | М, Н∙м | J , кг∙м2 | М1/М2 | ε 1/ ε 2 |
| 1 2 3 | |||||||||||
| Ср | ε 1 | M1 | |||||||||
| Шкив большего диаметра D2 | 1 2 3 | ||||||||||
| Ср | ε 2 | M2 |
Вторая часть: Момент сил, действующих на маятник, неизменен (в этом случае для приведения маятника во вращение нить с грузом m во всех измерениях наматывается только на один шкив). Грузы закрепляются последовательно на концах, середине стержней, а затем снимаются совсем. Тем самым изменяется момент инерции маятника в целом. Отношение моментов инерции при различных положениях грузов на стержнях должно быть равно обратному отношению соответствующих угловых ускорений.
2.6. Перенесите из таблицы 1 в таблицу 2 значения параметров m , h, a , ε, M для того шкива, который выбран во второй части работы.
2.7. Линейкой измерьте расстояние между центрами диаметрально расположенных на стержнях грузов и разделите это значение на два. Это будет расстояние от оси до центра грузов ri . Результата занесите в столбец ri табл. 3.
2.8. Сместите грузы на середину, добейтесь безразличного равновесия и снова измерьте уже новое значение ri. Снова внесите его в столбец ri таблицы 3.
2.9. Отпустите приводной груз m и измерьте время его несвободного падения. Результаты занесите в табл. 2.
2.10. Освободите маятник от грузов, и вновь проделав измерения времени несвободного падения, занесите его в таблицу 2..
2.11. Произведите вычисления. Убедитесь, что отношения угловых ускорений обратно пропорциональны отношению соответствующих моментов инерции 
.
2.12. Момент инерции величина аддитивная. Поэтому момент инерции маятника с грузами равен сумме момента пустого маятника (экспериментальное значение из табл. 2) и момента 4-х грузов, которые для приближенного расчета их момента инерции можно принять за материальные точки. Рассчитайте и сравните полученные значения моментов инерции с экспериментальными, заполняя соответствующие графы таблицы 3.
Таблица 2
| Маятник | N | m, кг | D , м | t, c | а, м/с2 | ε,с-2 | М, Н∙м | J | Jm/Jn | ε n / ε m |
| Грузы на концах | 1 2 3 | |||||||||
| Ср | ε 1 | J1 | ||||||||
| Грузы на середине | 1 2 3 | |||||||||
| Ср | ε 2 | J2 | ||||||||
| Без грузов | 1 2 3 | |||||||||
| Ср | ε 3 | J3 |
Таблица 3
| mi |
ri | Момент инерции J , кг ·м2 | |||
| Грузов | Маятник с грузами (вычисленный) | Маятник с грузами (экспериментальный) (из таблицы 2) | |||
| Грузы на середине | |||||
| Грузы на концах | |||||
3. Контрольные вопросы
3.1. Какое движение называется вращательным?
3.2. Сформулируйте второй закон Ньютона для вращательного движения. Сравните со вторым законом для поступательного движения.
3.3. Чему равен момент инерции тела правильной формы обруча, цилиндра, шара, стержня заданного размера и массы?
3.4. Чему равен момент инерции системы тел?
3.5. Сформулируйте теорему Штейнера.
ЛАБОРАТОРНАЯ РАБОТА № 4
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА
ДИНАМИЧЕСКИМ МЕТОДОМ
Цель работы: Знакомство с характеристиками и законами вращательного движения.
Приборы и материалы:
1. Маховое колесо.
2. Приводной груз.
3. Штангенциркуль.
4. Рулетка.
5. Секундомер.
1. Теоретическое введение
Вращательным называется такое движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Важнейшими характеристиками вращательного движения являются угловая скорость ω и угловое ускорение ε.
Угловой скоростью называется величина, равная изменению угла поворота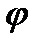 
твердого тела за единицу времени, т.е.
(1)
Угловое ускорение описывает быстроту изменения угловой скорости:
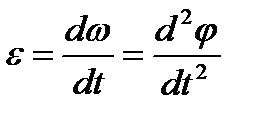(2)
Угловая скорость и угловое ускорение в процессе вращательного движения для всех частиц твёрдого тела одинаковы. Линейная скорость υ точки вращающегося тела связана с угловой скоростью соотношением:
(3)
где R - расстояние точки от оси вращения. Из этой формулы видно, что линейные скорости точек, находящихся на разном расстоянии R от оси вращения, различны.
Для описания динамики вращательного движения, использующихся в динамике поступательного движения понятий силы и массы, недостаточно. Действительно, если при поступательном движении определенная сила вызывает движение или вполне определенные изменения движения тела, то во вращательном движении результат действия силы зависит от того, на каком расстоянии от оси вращения она приложена. Произведение величины силы, приложенной к данной точке тела, на кратчайшее расстояние от оси вращения до направления вдоль которого она действует, называется моментом силы.
моментом силы
M = F·r (4)
Рис.1
Произведение массы i-ой материальной точки на квадрат расстояния от этой точки до оси вращения называется моментом инерции материальной точки.
Ji=mi·ri2 (5)
Момент инерции всего тела равен сумме моментов инерции составляющих его материальных точек
(6)
Так же как масса при поступательном движении определяет свойства инерции тела, момент инерции характеризует инертность тела при вращательном движении и зависит от распределения массы относительно оси вращения. По аналогии с поступательным движением, кинетическая энергия вращающегося тела равна:
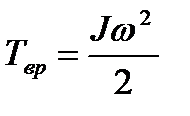(7)
Рассмотрим вращение твердого тела под действием приложенной к нему силы F. Выберем бесконечно малый промежуток времени t, такой, чтобы угловая скорость за этот промежуток не успевала увеличиваться и ее можно было бы считать постоянной. Тогда, двигаясь с постоянной угловой скоростью ω, за время dt тело повернется на угол d 
= ω dt . При этом точка приложения силы, находящаяся на расстоянии r от оси вращения, опишет дугу dS = rd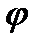 
. Элементарная работа в этом случае равна
dA = FdS = Frd 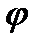= Fr ω dt (8)
При пренебрежимо малой величине силы трения эта работа по закону сохранения энергии вся расходуется на изменение кинетической энергии вращающегося тела, т.е.
(9)
Отсюда следует, что
Fr ω dt = J ω d ω (10)
Учитывая, что M = Fr , получаем Mdt = Jd ω или (при условии J =Const)
Mdt = d ( J ω)
Величина L = J ω называется моментом импульса (или по аналогии с поступательным движением) моментом количества вращательного движения. С учетом этого, последнее выражение можно переписать в виде: Mdt = dL или M = dL / dt , (11)
т.е. момент силы равен скорости изменения момента импульса (момента количества движения), вращающегося твердого тела. Это основной закон динамики вращательного движения. Закону можно придать и другую формулировку. Из (10) следует, что
, (12)
т.е. момент силы М,под действием которого вращается тело прямо пропорционален произведению величины момента инерции на угловое ускорение.
В настоящей работе, в качестве махового колеса, используется велосипедное, которое может вращаться вокруг горизонтальной оси, расположенной на высоте около 1,8 м от пола (см. рис. 1). На оси колеса укреплен шкив со шпилькой, на которую с помощью петли надевается шнур. К другому концу шнура привязан груз. Если вращать маховое колесо, то шнур накручивается на вал и груз поднимается на некоторую высоту. В этом случае вся система получает запас потенциальной энергии, равный произведению веса груза mg на высоту h его подъема. Если затем отпустить груз, то потенциальная энергия П будет превращаться в кинетическую энергию его поступательного движения Тпост, и кинетическую энергию вращения махового колеса Твр. На основании закона сохранения энергии можно записать:
П = Тпост + Твр (13)
С учетом того, что П = mgh ,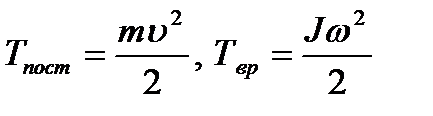 
уравнение (13) будет иметь вид
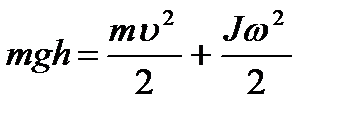. (14)
Так как шнур закреплен, намотан на шкив и движется вместе с ним без проскальзывания, то скорость поступательного движения шнура и груза равна линейной скорости точек, лежащих на поверхности шкива. Для определения этой скорости запишем уравнения равноускоренного движения для скорости υ и изменения высоты h груза во времени
υ = at и h = at 2 /2;
объединяя которые получим
(15)
Используя формулы (3) и (15) находим выражение для угловой скорости всех точек колеса
(16)
Подставляем найденные значения υ и ω в (14) и получаем:
(17)
После сокращения на h и элементарных преобразований получим расчетную формулу для экспериментального определения момента инерции махового колеса:
(18)
Так как удобнее измерять не радиус, а диаметр D = 2 r, формулу (18) можно переписать в окончательном виде:
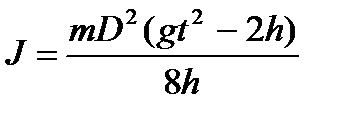(19)
Это выражение используется для косвенного измерения момента инерции махового велосипедного колеса в настоящей работе.
2. Порядок выполнения работы
2.1. Взвесьте груз с помощью весов.
2.2. Измерьте штангенциркулем диаметр шкива в месте намотки шнура.
2.3. Измерьте высоту h поднятия груза, которая равна расстоянию от подвижной планки, на которую ставится груз, до пола или подставки.
2.4. Наденьте петлю шнура на шпильку шкива, намотайте на него шнур, поставьте груз на откидную планку. Нажав на пусковой механизм планки, одновременно пустите в ход секундомер, и измерьте время опускания груза.
2.5. Опыт повторите 3 раза, и результаты всех измерений занесите в табл. 1.
2.6. Подставьте средние значения измеряемых величин в формулу (19) и рассчитайте средний момент инерции махового колеса.
2.7. Определите относительную и абсолютную погрешности полученного значения момента инерции
2.8. Результат измерений запишите в виде с указанием размерности момента инерции
J изм=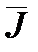 
±Δ 
Таблица 1
| Высота поднятия груза, (м) | Диаметр шкива, (мм) | Масса груза, (г) | Время падения груза, (сек) | |||||
| h | Δ h | D | Δ D | m | Δ m | t | Δ t | |
| 1 2 3 Ср еднее | ||||||||
3. Контрольные вопросы
3.1. Какое движение называют вращательным?
3.2. Какие физические величины характеризуют вращательное движение? В каких единицах они измеряются?
3.3. В каких единицах измеряются угловая скорость и угловое ускорение?
3.4. Какая связь между линейными и угловыми скоростями и ускорениями?
3.5. Напишите и сформулируйте основной закон динамики вращательного движения?
3.6. Каков физический смысл инерции?
3.7. Приведите формулы моментов инерции некоторых тел правильной формы.
3.8. Выведите формулу, используемую для косвенного измерения момента инерции
махового колеса в настоящей работе.
ЛАБОРАТОРНАЯ РАБОТА № 9
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ПРИ ПОМОЩИ
ПРУЖИННОГО МАЯТНИКА
Цель работы: Определение параметров затухающих колебаний пружинного маятника.
Приборы и принадлежности:
1. Пружинный маятник.
2. Секундомер.
3. Набор грузов.
4. Метрическая шкала.
1. Теоретическое введение
Колебания, совершаюшиеся без воздействия внешней периодической силы в результате какого-либо начального отклонения системы из положения равновесия, называется свободными.
Если вследствие наличия сил трения амплитуда свободных колебаний с течением времени уменьшается, то такие колебания называются затухающими. Затухающие колебания, вообще говоря, не являются периодическими, т.к. максимальные значения смещения скорости и ускорения в них никогда не повторяются. Поэтому периодом затухающих колебаний принято называть время между двумя последовательными переходами грузом положения равновесия при движении в одном и том же направлении.
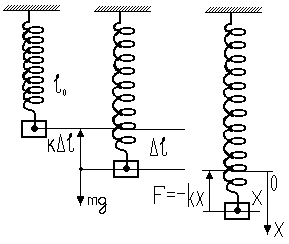Мы будем изучать затухающие колебания на примере пружинного маятника, представляющего собой груз массой m, колеблющийся на упругой пружине (рис. 1).
Когда груз висит на пружине (средняя часть рис.1), его вес уравновешивается силой упругости, обусловленной статическим растяжением пружины на величину ΔL под действием силы тяжести
mg = k ∙ΔL,
где k – коэффициент упругости, а ΔL удлинение пружины после навешивания груза.
Если груз дополнительно оттянуть на некоторое расстояние х=Δl (правая часть рис.1), то возникает возвращающая сила (сила упругости пружины), пропорциональная этому смещению
F = - kx. (1)
Рис.1
Под действием этой силы груз будет совершать колебательное движение вокруг статического положения. При этом отклонение от положения равновесия вверх и вниз будут одинаковыми.
При небольших скоростях, силы вызывающие затухание, можно считать пропорциональными величине скорости
F = - r ∙ υ (2)
где r – коэффициент сопротивления. Знак «минус» указывает на то, что сила сопротивления направлена против смещения. Таким образом, мы приходим к дифференциальному уравнению затухающих колебаний:
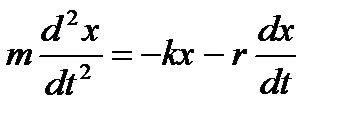
или
(3)
Решение дифференциального уравнения (3) имеет вид:
(4)
где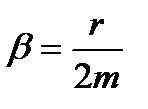 
- коэффициент затухания;
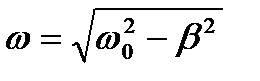- циклическая частота затухающих колебаний;
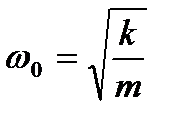- циклическая частота собственных колебаний.
Период затухающих колебаний определяется равенством:
(5)
Затухающие колебания можно рассматривать, как гармонические с уменьшающйся по экспоненциальному закону амплитудой (Рис.2):
(6)
где е = 2,718 – основание натуральных логарифмов.
Пусть в течение промежутка времени t амплитуда затухающих колебаний уменьшается в e раз. Тогда для отношения амплитуд колебаний, разделенных этим промежутком времени t можно записать
Из этого равенства β∙t = 1 или
β = 1/t (7)
Рис.2
Таким образом, коэффициент затухания обратно пропорционален времени, в течение которого амплитуда затухающих колебаний уменьшается в e раз. Мерой затухания колебаний является логарифмический декремент затухания δ, который равен натуральному логарифму отношения двух последовательных амплитуд, разделенных временным интервалом в один период колебаний:
(8)
Подставляя β из (7) в последнее выражение получаем:
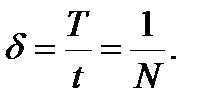(9)
Т.е. логарифмический декремент равен обратной величине числа колебаний, по истечении которых амплитуда уменьшается в e раз.
Амплитуда N-го колебания связана с амплитудой начального следующим образом:
(10)
Отсюда получаем формулу для экспериментального определения логарифмического декремента затухания
(11)
2. Порядок выполнения работы
2.1. Снять по шкале отсчет, соответствующий положению основного груза пружинного маятника.
2.2. Взвесить основной и добавочный груз. Результаты записать.
2.3. Подвесить добавочный груз и снять отсчет, соответствующий удлинению пружины. Опыты провести по три раза для разных добавочных грузов.
2.4. По известным массам и соответствующим удлинениям определить коэффициент жесткости пружины. Определить среднее значение k.
2.5. Оттянув груз маятника вниз, задать начальную амплитуду А0 и отпустить груз. Определить время N полных колебаний и а А0мплитуду N – го колебания А N по формуле (10). Опыт повторить 3 раза для значений А0 = 5,6,7 см и соответственно N = 50, 100, 150 колебаний. Результаты измерений занести в таблицу.
2.6. Для всех значений амплитуды А0 пункта 2.5. вычислить по формуле (11) логарифмический декремент δ и период затухающих колебаний 
. Найти их средние значения и занести в таблицу.
2.7. Используя средние значения δ и Т, по формуле (8) определить коэффициент затухания β. Результат занести в таблицу.
2.8. Вычислить период собственных колебаний по формуле:
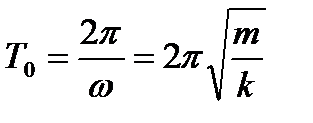
и сравнить с измеренным значением T, полученным в пункте 2.6.
2.9. Зная массу груза m и коэффициент затухания β, определить коэффициент сопротивления r = 2 m β.
Таблица 1
| № опыта | А0, см | AN , см | N | t , с | T=t / N | δ | β , с-1 | r , кг/с | Т0, с | k , кг/с2 |
| 1 2 3 Среднее | 100 150 200 |
3. Контрольные вопросы
3.1. Какие колебания называются затухающими?
3.2. Что называется логарифмическим декрементом затухания?
3.3. Каков физический смысл коэффициента затухания β и логарифмического декремента δ?
ОГЛАВЛЕНИЕ
1. Введение .....................................................................................................................стр. 2
2. Элементы теории погрешностей ..............................................................................стр. 3
3. №1. Определение плотности твердого тела правильной формы………… …….стр. 7
4. №2 Определение ускорения силы тяжести по способу Бесселя…..............……стр. 10
5. №3 Определение ускорения силы тяжести при помощи пружинного
маятника.............................................................................................................стр. 15
6. №4 Физический оборотный маятник…………… ………………………………стр. 24
7. №5 Определение момента инерции физического маятника в виде
однородного стержня ………………………………………………..………..стр. 28
8. №6 Определение момента инерции маховика и силы трения в опоре ……......стр. 29
9. №7 Изучение основного закона вращательного движения с помощью
маятника Обербека ……………………………………………...…………….стр. 36
10. №8 Определение момента инерции махового колеса динамическим
методом.........................................................................................................…...стр. 40
11. №9 Изучение затухающих колебаний .……………………………………… …..стр. 44
Дата добавления: 2021-02-10; просмотров: 397; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!