ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПО СПОСОБУ БЕССЕЛЯ

⇐ ПредыдущаяСтр 2 из 6Следующая ⇒

Цель работы: Экспериментальное изучение гармонических колебаний с помощью математи-

ческого маятника.

Определение ускорения силы тяжести по способу Бесселя.

Приборы и принадлежности:

1. Математический маятник.

2. Секундомер.

3. Отсчетная шкала.

1. Теоретическое введение

Колебаниями называется процессы, характеризующие повторяемость во времени. В механике примерами таких явлений могут служить колебания маятников, струн, мембран, камертонов, судна на волне и т.д. Если изменяющаяся в процессе, колебаний физическая величина х принимает определенные значения через равные промежутки времени, то такие колебания является периодическими.

Частным случаем периодических колебаний являются гармонические колебания, в которых изменение физической величины происходит по гармоническому закону, т.е. по закону синуса или косинуса:

(1)

или

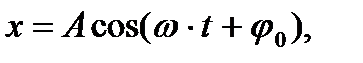
Здесь х - смещение из положения равновесия;

А - амплитуда (максимальное смещение);

φ₀ - начальная фаза, соответствующая моменту начала колебаний t = 0;

(ω∙t + φ_о) - фаза колебаний; она состоит из начальной φ_о(фиксированной) и фазы ω∙t, увеличивающейся пропорционально времени колебаний.

ω - циклическая (или круговая) частота.

Время, в течение которого совершается одно полное колебание, называется периодом Т, а число колебаний за единицу времени (в системе СИ за одну секунду) - частотой колебаний

(2)

Другими словами частота это количество периодов колебаний укладывающихся в интервале времени равном одной секунде.

Поскольку период гармонических функций равен 2π, то циклическую частоту можно представить в виде:

(3)

Таким образом, циклическая частота равна числу колебаний укладывающихся в интервале 2π секунд.

Скорость υ и ускорение a при колебательном движении выражаются соответственно первой и второй производной по времени от смещения х (см. 5 и 6). Если смещение задано в гармоническом виде:

, (4)

то

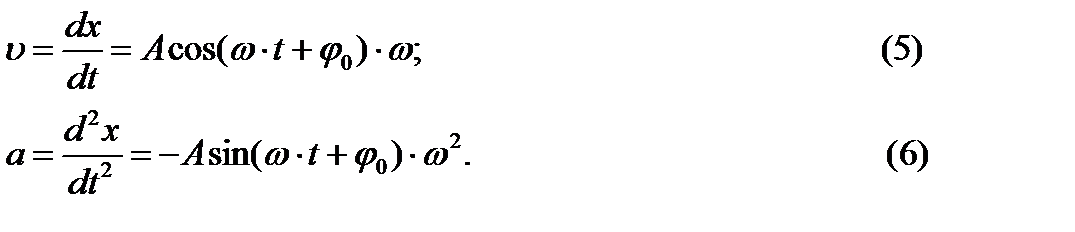
С учетом формулы (4) последнее уравнение можно записать:

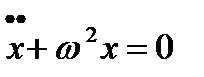(7)

Оно представляет собой дифференциальное уравнение гармонического осциллятора. Здесь двумя точками обозначена вторая производная по времени от смещения х.

Гармоническим осциллятором принято называть любую систему, колебательный процесс которой описывается дифференциальным уравнением вида (7). Не трудно видеть, что уравнение (4) является решением дифференциального уравнения гармонического осциллятора.

В качестве примера рассмотрим гармонические колебания математического маятника.

Математическим маятником называется материальная точка, колеблющаяся на невесомой и нерастяжимой нити. Материальная точка это простейшая физическая модель в механике, а именно: тело обладающее массой, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.

Чтобы найти уравнение движения маятника рассмотрим динамику колебательного процесса. Силу тяжести, действующую на материальную точку можно разложить на две составляющие: одна из которых P_n (она называется нормальной компонентой силы тяжести)направлена вдоль нити и уравновешивается силой натяжения F_n ; вторая - Р_τ - перпендикулярна к нити и направлена по касательной к траектории движения (она называется тангенциальной компонентой). Векторная сумма этих двух сил равна вектору силы тяжести P.

Составляющая Р_τ является квазиупругой силой, под действием которой совершаются колебания.

Если нить отклонена от положения равновесия на угол α, то тангенциальная компонента

Р_τ = - Р∙ sin α = - m ∙ g ∙ sin α (8)

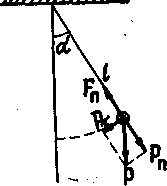
рис.1

Знак минус в формуле (8) указывает на то, что направление действия силы Р_τ противоположно направлению увеличения угла 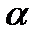. Рассматривая уравнение (8) для малых углов, для которых sin 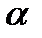≈ 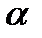, получаем:

(9)

Умножим уравнение (9) на длину нити l:

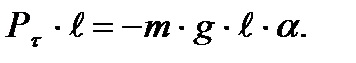(10)

В левой части выражения (10) мы имеем классический момент силы Р_τ , приложенной к плечу 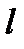, который можно в соответствии c основным законом динамики вращательного движения выразить еще и через момент инерции P _τ · l = M = J ·ε . Здесь ε угловое ускорение. После подстановки в (10) получаем

(11)

Подставляя значение момента инерции материальной точки J=ml² и, проводя элементарные преобразования, получим:

(12)

Таким образом, процесс колебания математического маятника для малых углов описывается дифференциальным уравнением гармонического осциллятора (12).

Из сравнения уравнений (12) и (7) находим, что

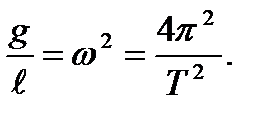
Выражая Т из этого уравнения, получаем классическую формулу для определения периода колебаний математического маятника

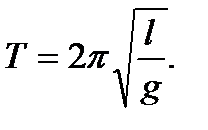(13)

Для определения ускорения свободного падения из этой формулы достаточно измерить период колебаний Т и расстояние l от точки подвеса до центра тяжести тела с сосредоточенной массой

Однако измерение длины нити l не всегда является удобным, из-за трудностей определения положения центра тяжести тела, особенно, если оно не является сферически симметричным. Этих трудностей можно избежать, если воспользоваться способом Бесселя. Этот способ заключается в использовании для измерений одного и того же маятника при двух различных длинах нити. Если определить периоды колебаний для маятника разной длины и удлинение нити математического маятника (разность длин), то можно определить ускорение силы тяжести не измеряя абсолютного значения длины нити маятника.

Действительно, используя формулу (13) дважды для математических маятников с длинами l ₁ и l ₂ соответственно получаем для квадратов периодов

;

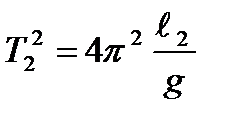
Вычитая из первого уравнения второе и разрешая относительно g, получаем

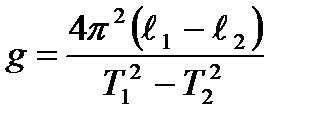(14)

В эксперименте с помощью специального устройства изменяют длину нити математического маятника, а по вертикальной неподвижно закрепленной линейке измеряют лишь удлинение нити l ₁ – l ₂ = h , не измеряя длин самих нитей. Удлинение соответствует разности двух отсчетов положения груза маятника, для нитей разной длины. Тогда формула (14) превращается в формулу, соответствующую методу Бесселя и используемую в данной работе для нахождения ускорения силы тяжести

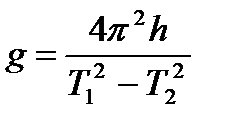. (15)

2. Порядок выполнения работы

2.1. Взять возможно большую длину маятника и сделать отсчет (h₁) положения груза маятника по шкале.

2.2. Вывести маятник из положения равновесия так, чтобы угол отклонения составлял (4-6)° и отпустить. Автоматическое устройство начнет отсчет времени и числа колебаний. При достижении 50 колебаний отсчет времени прекратится. Полученные значения времени и числа колебаний занести в таблицу1.

Для данной длины маятника опыт повторить три раза и все результаты намерений занести в таблицу1.

Таблица 1

№ пп	Длинный маятник					Короткий маятник
№ пп	Отчет по шкале h ₁ , см	Абсолют. ошибка, Δ h₁ , см	Время 50 колебаний, сек	Период одного колебания Т₁, с	Абсолют. ошибка, ΔТ₁, сек	Отчет по шкале h ₂ , См	Абсолют. ошибка, Δ h₂ , см	Время 50 колебаний, сек	Период одного колебания Т₂, с	Абсолют. ошибка, ΔТ₂, сек	Разность длин, h , см
1 2 3
Ср.

2.3. Укоротить длину нити маятника на 80-90 см, сделать отсчет (h₂) нового положения груза и повторить измерения пункта 2.2.

2.4. Определить средние значения величин Т₁, Т₂, h = h ₁ – h ₂ и, подставляя полученные средние значения в формулу (15) вычислить ускорение g _ср.

2.5. Определить относительную и абсолютную погрешности соответственно по формулам

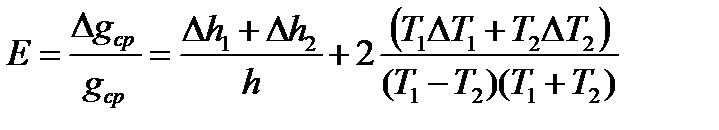(16)

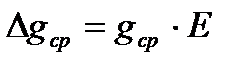17)

2.6. Результаты измерений представить в виде

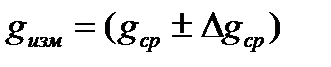
3. Контрольные вопросы

3.1. Какие колебания называется гармоническими? Напишите уравнение гармонических колебаний.

3.2. Дайте определение математического маятника.

3.3. Выведите формулу периода колебаний математического маятника. Почему этой формулой можно пользоваться только в том случае, когда амплитуда колебаний мала?

3.4. Почему в данной работе для определения ускорения силы тяжести измеряют периоды и разность длин двух математических маятников.

3.5. Выведите формулы (16) и (17) в соответствии с правилами обработки результатов косвенных измерений.

ЛАБОРАТОРНАЯ РАБОТА № 3

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ

ПРУЖИННОГО МАЯТНИКА

Цель работы: Экспериментальное изучение гармонических колебаний с

помощью пружинного маятника.

Определение ускорения силы тяжести при помощи пружинного

маятника.

Приборы и принадлежности :

1. Пружинный маятник.

2. Дополнительные грузы.

3. Секундомер.

4. Метрическая шкала.

Материал для изучения :

Механические гармонические колебания.

Колебания под действием упругой силы.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Механические гармонические колебания под действием упругой силы, рассмотрим на примере вертикального пружинного маятника. Пружинный маятник представляет собой груз массы m (рис.1), подвешенный на абсолютно упругой пружине. Упругие свойства пружины характеризуются коэффициентом упругости k. Когда груз находится в равновесии его вес равен силе упругости пропорциональной удлинению пружины под действием силы тяжести

mg = kΔl (1)

Если груз оттянуть на величину x, то на него начнет действовать возвращающая сила F =- kx. По второму закону Ньютона , ma = F. Таким образом, уравнение движения пружинного маятника имеет вид:

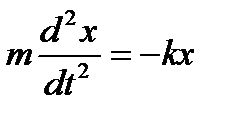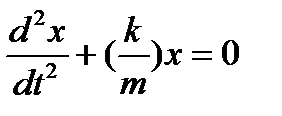или (2)

Это уравнение является дифференциальным уравнением гармонических колебаний, решением которого является 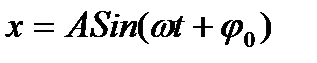, где ω циклическая частота собственных колебаний, равная ω²= k / m , а φ₀ начальная фаза колебаний. Следовательно период колебаний идеального пружинного маятника будет равен T =2 π / ω или

(3)

Полученное выражение для периода свободных колебаний пружинного маятника справедливо в предположении, что масса пружины много меньше массы груза, подвешенного на ней и амплитуда колебаний мала.

Дата добавления: 2021-02-10; просмотров: 1007; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!