Глава X ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Пусть функция f (х) определена на отрезке [а, b ]. Разделим отрезок [а, b ] на п произвольных частей точками а = х0 < х1 < x2 < ... < хп-1 < хп = b, выберем на каждом элементарном отрезке [xk-1, xk] произвольную точку ξk и найдем длину каждого такого отрезка:  .
.
Интегральной суммой для функции f ( x ) на отрезке [ a , b ] называется сумма вида  ,причем эта сумма имеет конечный предел I , если для каждого ε>0 найдется такое число δ>0, что при мах ∆ xk < δ неравенство |σ- I |< ε выполняется при любом выборе чисел ξk .
,причем эта сумма имеет конечный предел I , если для каждого ε>0 найдется такое число δ>0, что при мах ∆ xk < δ неравенство |σ- I |< ε выполняется при любом выборе чисел ξk .
Определенным интегралом or функции f (х) на отрезке [а, b ] (или в пределах от а до b) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков (мах ∆ xk) стремится к нулю:

Если функция f ( x ) непрерывна на [a, b ], то предел интегральной суммы существует и не зависит от способа разбиения отрезка [а, b ] на элементарные и от выбора точек ξk . (теорема существования определенного интеграла).
Числа a и b соответственно называются нижним и верхним пределами интегрирования.
Если f(x)>0 на [а, b ], то определенный интеграл  геометрически представляет собой площадь криволинейной трапеции — фигуры, ограниченной линиями y = f ( x ), x = a , х = b , у = 0 (рис. 42).
геометрически представляет собой площадь криволинейной трапеции — фигуры, ограниченной линиями y = f ( x ), x = a , х = b , у = 0 (рис. 42).
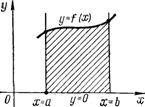
Рис. 42
Основные свойства определенного интеграла
1°. 
2°. 
3°. 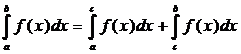
4°. 
5°.  , где С- постоянная
, где С- постоянная
6°. Оценка определенного интеграла: если  на [ a, b ], то
на [ a, b ], то
m ( b - a )<  < M ( b - a )
< M ( b - a )
Правила вычисления определенных интегралов
1. Формула Ньютона — Лейбница:

где F (х) — первообразная для f ( x ), т. е. F '( x )= f ( x ).
2. Интегрирование по частям:

где и = и(х), v = v (х) — непрерывно дифференцируемые функции на отрезке [а, b ].
3. Замена переменной:
где x =φ( t ) — функция, непрерывная вместе со своей производной φ ' ( t ) на отрезке  , a =φ( α ), b = φ( β ), f [φ( t )]— функция, непрерывная на [ α, β ].
, a =φ( α ), b = φ( β ), f [φ( t )]— функция, непрерывная на [ α, β ].
4. Если f (х) — нечетная функция, т. е. f (- х) =- f (х), то

Если f (х) — четная функция, т. е. f (- x )= f ( x ), то

1538. Вычислить интеграл 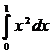 , как предел интегральной суммы.
, как предел интегральной суммы.
Решение. Здесь f ( x ) = x 2 , а = 0, b = 1; разделим отрезок [0, 1] на n равных частей, тогда 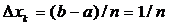 , выберем ξk =xk. Имеем:
, выберем ξk =xk. Имеем:
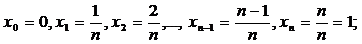
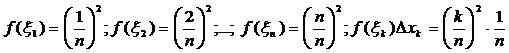 ;
;
Следовательно,

Здесь использована формула суммы квадратов натуральных чисел.
1539. Вычислить  по формуле Ньютона — Лейбница.
по формуле Ньютона — Лейбница.
Решение.
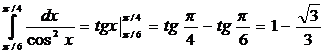
1 540 . Оценить интеграл 
Решение. Так как |cos x|≤1, то при x>10 получим неравенство  <10-2. Следовательно,
<10-2. Следовательно,
 <8* 10-2< 10- 1, т. е.
<8* 10-2< 10- 1, т. е.  <0,1
<0,1
1541. Оценить интеграл 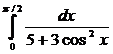
Решение. Поскольку 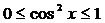 , имеем
, имеем
 и
и 
15 42 . Вычислить  .
.
Решение. Воспользуемся методом интегрирования по частям. Положим и = х, dv = e - x dx , откуда du = dx , v = — е- x . Тогда
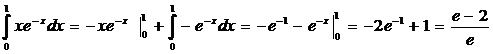
1543. Вычислить 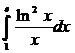
Решение. Положим ln x = t , тогда ( dx )/ x = dt, если x =1, то t =0; если x = e, то t =1
Следовательно,

1544. Вычислить 
Решение. Положим x = r sin t ; тогда dx = r cos t dt ; если x = 0, то t =0; если х = r , то t = π /2. Поэтому

1545. Вычислить 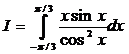
Решение. Подынтегральная функция — четная, а потому 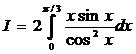
Интегрируем по частям, полагая и = х,  ; тогда du = dx , v =1/ cosx
; тогда du = dx , v =1/ cosx
Отсюда находим
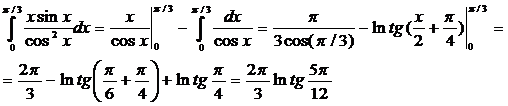
Следовательно,

1546. Вычислить  .
.
Решение. Подынтегральная функция—нечетная, следовательно, I= 0.
1547. Вычислить  как предел интегральной суммы.
как предел интегральной суммы.
1548. Вычислить  как предел интегральной суммы.
как предел интегральной суммы.
1549. Оценить интеграл  .
.
1550. Оценить интеграл 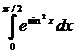 .
.
1551. Оценить интеграл  .
.
Вычислить интегралы:
1552.  1553 .
1553 . 
1554.  1555.
1555. 
1556.  1557.
1557. 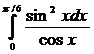
1558.  1559.
1559. 
1560.  1561.
1561. 
1562. 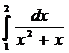 1563.
1563. 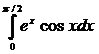
1564. 
Указание: использовать свойство нечетной функции.
1565. 
Указание: использовать свойство четной функции.
15 66 . Доказать, что



( m и n —целые положительные числа).
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
1. Основные понятия. Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций.
Несобственный интеграл от функции f ( x ) в пределах от a до + ∞ определяется равенством

Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если же предел не существует или равен бесконечности, - расходящимся.
Аналогично
 и
и 
Если функция f (х) имеет бесконечный разрыв в точке с отрезка [а, b ] и непрерывна при а ≤ х < с и с < x ≤ b , то, по определению, полагают
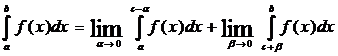
Несобственный интеграл 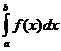 (где f (с)=∞, a < c < b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.
(где f (с)=∞, a < c < b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.
1567. Вычислить несобственный интеграл 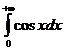 (или установить его расходимость).
(или установить его расходимость).
Решение. Имеем

т. е. предел не существует. Следовательно, несобственный интеграл расходится.
1568. Вычислить 
Решение. Найдем

т. е. несобственный интеграл сходится.
1569. Найти 
Решение. Подынтегральная функция— четная, поэтому 
Тогда

Таким образом,  , т. е. несобственный интеграл сходится.
, т. е. несобственный интеграл сходится.
1570. Найти 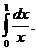
Решение. Подынтегральная функция f (х)= 1/х в точке x = 0 неограниченна, а потому имеем

т. е. несобственный интеграл расходится.
1571. Найти 
Решение. Имеем
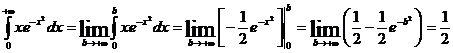
т. е. несобственный интеграл сходится.
Вычислить несобственные интегралы:
1572. 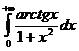 1573.
1573. 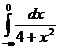
1574.  1575.
1575. 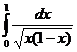 1576.
1576. 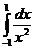
1577.  1578.
1578. 
2. Признаки сравнения. При исследовании сходимости несобственных интегралов пользуются одним из признаков сравнения.
1. Если функции f (х) и φ( x ) определены для всех х≥а и интегрируемы на отрезке [а, А], где А≥а, и если 0≤f(х)≤φ( x ) для всех х≥а, то из сходимости интеграла 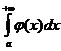 вытекает сходимость интеграла
вытекает сходимость интеграла  , причем
, причем
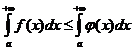
2. (а) Если при x→+∞ функция f ( x )≥0 является бесконечно малой порядка р > 0 по сравнению с 1/ x, то интеграл  сходится при р > 1 и расходится при р≤1.
сходится при р > 1 и расходится при р≤1.
(б) Если функция f ( x ) ≥0 определена и непрерывна в промежутке а ≤ х< b и является бесконечно большой порядка р по сравнению с1/( b - x ) при х→b — 0, то
интеграл 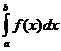 сходится при р < 1 и расходится при р≥ а
сходится при р < 1 и расходится при р≥ а
1579. Исследовать сходимость интеграла 
Решение. По определению

Допустим, что р>1; тогда 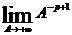 = 0. Значит, при р>1 интеграл сходится. Пусть р≤1; тогда
= 0. Значит, при р>1 интеграл сходится. Пусть р≤1; тогда  , т. е. интеграл
, т. е. интеграл  при р ≤ 1 расходится.
при р ≤ 1 расходится.
1580. Исследовать сходимость интеграла 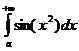 (интеграл Френеля).
(интеграл Френеля).
Решение. Пусть 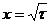 , тогда
, тогда  . Представим стоящий справа интеграл в виде суммы:
. Представим стоящий справа интеграл в виде суммы:

Первое слагаемое есть собственный интеграл, так как 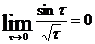 , а ко второму применим интегрирование по частям, полагая
, а ко второму применим интегрирование по частям, полагая  :
:

Последний интеграл сходится, так как  , а интеграл
, а интеграл 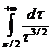 сходится.
сходится.
Поэтому 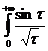 сходится на основании признака (2а), а следовательно, данный интеграл также сходится.
сходится на основании признака (2а), а следовательно, данный интеграл также сходится.
15 81 . Исследовать сходимость интеграла  .
.
Решение. Подынтегральная функция f ( x )=1/(1+ x 10 ) в промежутке интегрирования меньше, чем φ(х)=1/х10, а интеграл 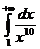 является сходящимся.
является сходящимся.
Следовательно, данный интеграл также сходится.
1582. Исследовать сходимость интеграла  ( a < b ).
( a < b ).
Решение. По определению

Если р<1, то  ; если же p> 1, то
; если же p> 1, то 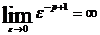 ; если, наконец, p = 1 , то
; если, наконец, p = 1 , то

Следовательно, при р<1 интеграл  сходится, а при р≥1 – расходится.
сходится, а при р≥1 – расходится.
1583. Исследовать сходимость интеграла 
Решение. Подынтегральная функция является бесконечно большой при х → 1 . Представим ее в следующем виде:
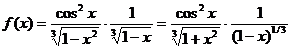
т. е. порядок этой бесконечно большой функции при х→1 по сравнению с 1/(1 - x ) равен р=1/3 < 1. Поэтому данный интеграл сходится на основании признака (2б).
1584. Исследовать сходимость интеграла  .
.
Решение. Подынтегральная функция f (х) в промежутке интегрирования положительна и f (х) → ∞ при х →0. Пользуясь теоремой об эквивалентных бесконечно малых, преобразуем числитель и знаменатель подынтегральной дроби: имеем 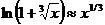 , а
, а  при х→0, откуда
при х→0, откуда

т. е. f (х) является бесконечно большой порядка р = 2/3 по сравнению с 1/х. Следовательно, по признаку (2б) заданный интеграл сходится.
Исследовать сходимость следующих несобственных интегралов:
1585.  1586.
1586. 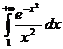 1587.
1587. 
1588. 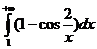 1589.
1589. 
1590.  1591.
1591. 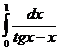
Дата добавления: 2021-01-20; просмотров: 109; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
