Векторное произведение в координатной форме.

a ´ b= (a_xi + a_yj + a_zk)×( b_xi + b_yj + b_zk)= a_x b_x i× i + a_x b_y i× j + a_x b_z i ×k +

+a_y b_x j×i + a_y b_y j×j + a_y b_z j×k + a_z b_x k×i + a_z b_y k× j + a_z b_z k×k=

= a_x b_y k – a_x b_z j- -a_y b_x k+ a_y b_z i+ a_z b_x j - a_z b_y i=

= i(a_y b_z - a_zb_y )- j( a_x b_z - a_z b_x)+ k(a_x b_y - a_y b_x )=

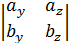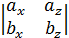=i  - j  + k .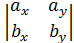

 .

 

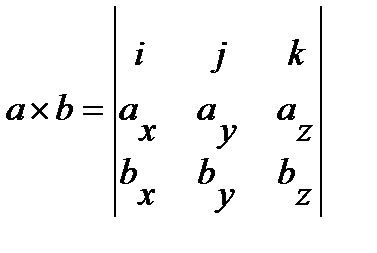Приложения векторного произведения.

1) Площадь параллелограмма, построенного на векторах a и b, как на сторонах, численно равна модулю векторного произведения a ´ b.

S _пар =│ a ´ b │.

Из геометрии: S _пар =│ a │·│ b │ sin φ.

Так как │ a ´ b │= │ a │·│ b │ sin φ, отсюда следует, что S _пар =│ a ´ b │.

Следствие: из геометрии S _пар =│ a ·│ h_a, ,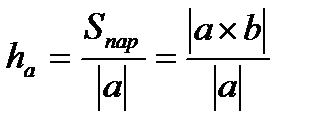

где h_a – высота, проведенная к стороне a .

2) .

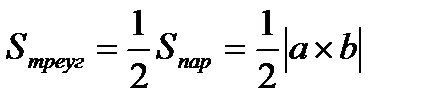ha

   

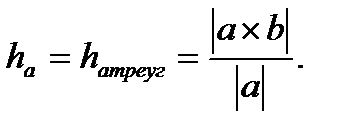
3) a║b. Отсюда следует, что a´b=0 (из условия коллинеарности двух векторов).

b

а

b

а

Ðj= 0°, sin 0°= 0   Ðj=180°, sin 180°= 0

│a´b│= │a│·│b│sin φ= 0,

│a´b│= 0.

Смешанное произведение трех векторов.

Определение: Смешанным произведением трех векторов a , b , c, взятых в таком порядке называется число, равное ( a ´ b )•с.

По определению: abc.

Чтобы вычислить смешанное произведение нужно:

1) вектор 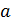умножить векторно на : a ´ b= вектор;

2) полученный вектор умножить на с скалярно: (a ´ b )•с= число.

 

Свойства смешанного произведения:

1° смешанное произведение вкруговую abc = - bac = bca = ...

2° ( λ a)bc= λ(abc).

3° (a+ b) cd= acd+ bcd.

4° ijk= (i×j)• k= k• k= │k│²= 1. ijk= 1.

 

Смешанное произведение в координатной форме.

Возьмем три вектора в координатной форме:

а= (а_х, а_у, а _z )= a_xi + a_yj + a_zk ;

b= (b_x, b_y, b_z)= b_xi + b_yj + b_zk;

с = ( с _x , с _y , с _z ) = c_xi + c_yj + c_zk.

abc= (a ´ b)• с.

 

.

 

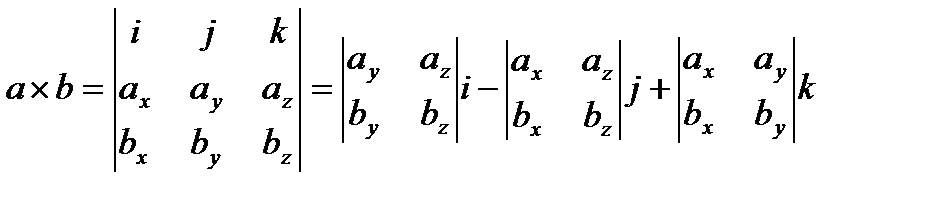
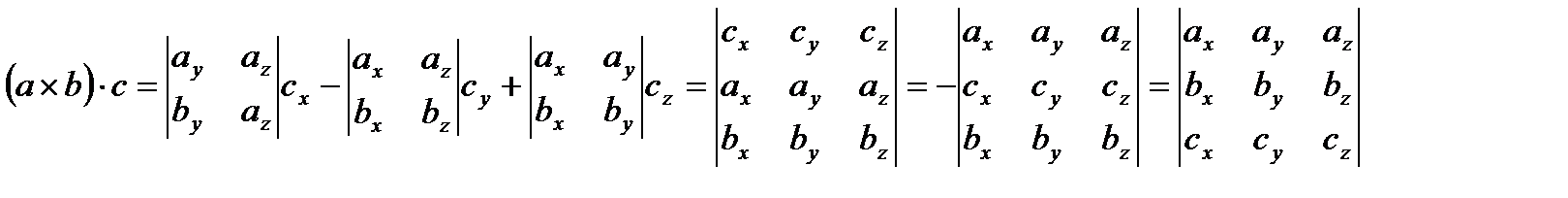
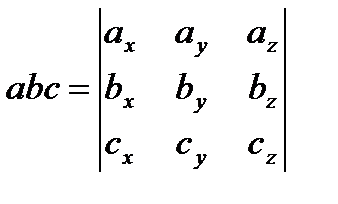Приложения смешанного произведения.

1) Модуль смешанного произведения численно равен объему параллелепипеда, построенного на трех векторах как на ребрах.

V _парал = │ abc │.

Из геометрии: V _парал = S _осн · h .

S _осн = S _пар =│ a ´ b │.

Из приложения векторного произведения:

h =│с│· cos φ .

V _парал = │ a ´ b │·│ c │· cos φ =│( a ´ b ) • с│=│ abc │.

Следствие: высота параллелепипеда h= .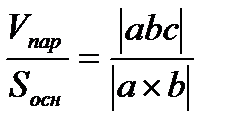

2) V _тетр = V _парал = │ abc │.

Из геометрии:  V _тетр = 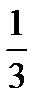S _осн · h; h _тетр = .

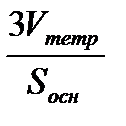3) Если смешанное произведение abc >0, то тройка векторов правая; если abc <0, то тройка векторов левая.

abc= (a ´ b) • с = │a ´ b│·│c│·cos φ.

abc >0, cos φ >0, Ðj- острый, abc - правая тройка.

abc <0, cos φ <0, Ðj- тупой, abc - левая тройка.

 

4) abc – компланарные, если параллельны одной плоскости или лежат в одной плоскости.

 

Условие компланарности: abc =0.

a ´ b ^ плоскости α.

a ´ b ^ с, ( a ´ b ) • с = 0 (условие перпендикулярности двух векторов), abc =0.

 

 

Задание вектора в пространстве.

Любой вектор в пространстве имеет длину и направление.

Длина вектора │а│= .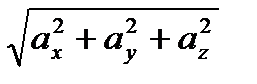

Направление вектора задают три направляющих косинуса: cos α, cos β, cos γ, где Ðα- угол между 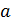 и ОХ, Ðβ- угол между a и ОУ, Ðγ- угол между a и OZ.

i

β

y

O

х

j

γ

k

z

α

Ð α = Ð (a,i), Ð β = Ð (a,j), Ð γ = Ð (a,k).

cos α= , cos β= 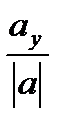, cos γ= .

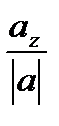Свойство направляющих косинусов:

cos² α+ cos² β+ cos² γ= 1.

Определение: Единичный вектор, имеющий своими координатами направляющие косинусы вектора a называется единичным вектором направления а и обозначается a₀= (cosα, cosβ, cosγ).

1

а

а0

 

Аналитическая геометрия.

Плоскость в пространстве.

Определение: Любой ненулевой вектор, перпендикулярный плоскости, называется вектором нормали к этой плоскости.

N = ( A , B , C ).

Пусть т. М₀ (x₀, y₀, z₀) - произвольная фиксированная точка плоскости α,

т. М (x, y, z) - произвольная нефиксированная точка плоскости α (текущая).

α

М0

М

 

Вектор М₀М=( x - x ₀ , y - y ₀ , z - z ₀ ) Є плоскости α.

Вектор N = ( A , B , C ) ^ плоскости α.

⇒ N ^ М₀М.

Из условия перпендикулярности двух векторов: N • М₀М= 0.

В координатной форме: A ( x - x ₀ )+ B ( y - y ₀ )+ C ( z - z ₀ )= 0 – уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

Раскроем в этом уравнении скобки и соберем свободные члены

Ax+By+Cz-Ax₀-By₀-Cz₀= 0.

Обозначим: D=-Ax₀-By₀-Cz₀.

Ax + By + Cz + D = 0 — общее уравнение плоскости, где  N ( A , B , C ) – координаты вектора нормали.

 

Анализ общего уравнения.

1) А= 0, B , C , D ≠ 0, т.е. нет х, нормаль N =(0, B , C ).

Скалярное произведение:  N • i = 0· 1+ B · 0+ C · 0= 0. ⇒ N ^ i , N ^ OX.

Т.о. плоскость параллельна оси OX , т.е. α ║OX .

Аналогично, В=0, нет у, плоскость α║ОУ;

                  С=0, нет z, плоскость α║OZ .

 

2) А= В= 0; нет х, у; плоскость α║XOY ;

A = C = 0; нет x , z; плоскость α║XOZ ;

В= С= 0; нет y , z; плоскость α║YOZ.

 

3) D = 0: Ax + By + Cz = 0.

т. О (0, 0, 0) удовлетворяет уравнению, плоскость проходит через начало координат т. О(0, 0, 0).

 

4) A = D = 0, B ≠ C ≠ 0, т.е. нет х и проходит через т. О. ⇒ плоскость α проходит через ОХ.

Аналогично, B = D = 0, плоскость α проходит через ОУ;

                 C = D = 0, плоскость α проходит через OZ .

 

5) х= 0 - уравнение координатной плоскости YOZ ;

y = 0 - уравнение координатной плоскости XOZ;

z = 0 - уравнение координатной плоскости XOY .

 

---

Дата добавления: 2019-09-13; просмотров: 194; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!