Скалярное произведение векторов в ортонормированном базисе.
Определение: Два вектора Евклидова пространства называются ортогональными, если их скалярное произведение равно нулю.
Определение: Базис Евклидова пространства l 1 , l 2 , ... , ln называется ортонормированным, если векторы l 1 , l 2 , ... , ln попарно ортогональны и длина каждого вектора равна 1, т.е.
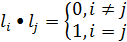 .
.
Пусть вектора x, y заданы своими координатами в ортонормированном базисе l 1 , l 2 , ... , ln:
х =(α1, α2,… α n )= α1 l 1 + α2 l 2 + ... +α n ln, у = (β1, β2, … β n )= β1 l 1 + β2 l 2 +…+β n ln.
Найдем их скалярное произведение:
x • y =(α1, α2,… α n )•(β1, β2, … β n )= (α1 l 1 + α2 l 2 + ... +α n ln )•( β1 l 1 + β2 l 2 +…+β n ln )=
= α1 l 1 •β1 l 1 + α1 l 1 •β2 l 2 +…+ α1 l 1 •β n ln + α2 l 2 •β1 l 1 + α2 l 2 •β2 l 2 +…+
+α2 l 2 •β n ln +…+ α n ln •β1 l 1 + α n ln •β2 l 2 +…+ α n ln •β n ln =
= α1 β1 ( l 1 • l 1 )+ α1 β2( l 1 • l 2 )+…+ α1 β n ( l 1 • ln )+ α2 β1( l 2 • l 1 )+ α2 β2( l 2 • l 2 )+…+
+ α2 β n ( l 2 • ln )+…+ α n β1( ln • l 1 )+ α n β2( ln • l 2 )+…+ α n β n ( ln • ln )=
=(учтем, что вектора l 1 , l 2 , ... , ln – ортонормированный базис)=
= α1 β1+ α2 β2+…+ α n β n.
Т.о. скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат.
Декартовая система координат.
Рассмотрим три ненулевых, не коллинеарных вектора в пространстве l 1 , l 2 , l 3- это базис ЛП V3. Приведем эти векторы к общему началу в точке О и расположим их по осям.
| l3 |
| l2 |
| z |
| у |
|
|
|
| O |
| l1 |
| х |
Определение: Совокупность точки и базиса называется декартовой системой координат.
Определение: Если базисные вектора взаимно перпендикулярны, длины их равны 1, то такой базис называется ортонормированным. Базисные вектора называются ортами и обозначаются i , j , k, а система координат называется декартовой прямоугольной системой координат.
| y |
| i |
| O |
| х |
| j |
| 1 |
| k |
| z |
Свойство орт:
1) i ┴ j, i ┴ k, j ┴ k;
2) │i│= │j│= │k│= 1.
Декартовых систем координат бесконечное множество.
Определение: Тройка векторов a , b , c называется правой, если кратчайший поворот от вектора a к b , видимый с конца вектора с будет против часовой стрелки.
Если такой поворот по часовой стрелке, то тройка векторов называется левой.
| правая тройка |
| с |
| b |
| а |
| а |
| b |
| с |
| левая тройка |
Мы будем рассматривать такие системы координат, в которых базисные вектора образуют только правую тройку.
Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора.
Возьмем в пространстве произвольную точку М(х, у, z ). Первая координата х – абсцисса ‒ это проекция т. М на ось ОХ. Вторая у – ордината – это проекция т. М на ось ОУ. Третья z – аппликата – на ось OZ.
|
|
|
| М |
| α |
| N |
Проекция т. М на α
Чтобы найти проекцию точки на прямую, нужно через точку провести плоскость перпендикулярно этой прямой.
| p |
| х |
| z |
| у |
| О |
| М (х, у, z) |
Определение: Вектор, соединяющий начало координат т. О с произвольной точкой пространства называется радиус- вектор этой точки.
Радиус- вектор т. М – ОМ.
Найдем координаты радиус-вектора ОМ:
ОА= xi , ОВ= yj , ОС= zk .
OM= OP+ PM= OA+ OB+ OC= xi+ yj+ zk= (x, y, z).
Вывод: координаты радиус-вектора точки совпадают с координатами самой точки ОМ= (x, y, z).
Вектор ОМ является диагональю параллелепипеда, по свойству диагоналей d2= a2+ b2+ c2 . Отсюда следует, что │ОМ│2= x2+ y2+ z2. Извлекая, квадратный корень получаем длину 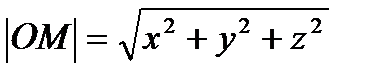 .
.
Возьмем две произвольные точки т. А(x1, y1, z1) и т. В (x2, y2, z2). Соединим АВ.
| B |
| А |
| z |
| х |
| y |
| O |
Вспомогательные векторы: ОА= (x1, y1, z1), ОВ= (x2, y2, z2).
АВ= ОВ - ОА= (x2, y2, z2)- (x1, y1, z1)= (x2- x1, , y2- y1, z2- z1).
Вывод: чтобы найти координаты вектора нужно из координат конца вектора вычесть соответствующие координаты начала вектора.
АВ = (x2- x1, , y2- y1, z2- z1).
Пример . Даны 3 точки т. А(2,-1,3), т. В(4,0,1), т. С(-1,2,1). Найти АВ и его длину │АВ│, m= AB- 2BC.
|
|
|
Проекция вектора на ось.
Определение: Проекцией вектора на ось называется число, модуль которого равен проекции на эту ось отрезка, задающего вектор, причем число берется со знаком «+», если координата конца вектора больше координаты начала вектора, и со знаком «-», если координата начала больше координаты конца.
Через т. А и т. В проведем плоскости перпендикулярныеоси l, и найдем точки пересечения плоскости с осью.
Перенесем вектор АВ в точку А1. А1В1(проекция)=АВ. Из прямоугольного треугольника следует, что проекция АВ на ось l будет равна:
│АВ│· cos φ= пр l AB.
пр l AB=│АВ│· cos φ, где φ - это угол между вектором и осью.
Возможны 3 случая:
1) Ðφ- острый, пр l AB> 0, т.к. cos φ> 0.
| l |
| φ |
| В |
| А |
2) Ðφ- тупой, пр l AB< 0, т.к. cos φ< 0.
| A |
| B |
| φ |
| l |
3) Ðφ= 90°, пр l AB= 0, т.к. cos φ= 0.
| A |
| B |
| φ |
| l |
Теоремы о проекциях.
Теорема 1. пр l(а + b)= пр l a + пр l b.
Теорема 2. пр l (λа)= λ пр l а.
Дата добавления: 2019-09-13; просмотров: 310; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
