Ответы к заданиям с кратким ответом
Геометрия
| № задания | Ответ |
| 1 | 12 |
| 2 | 5 |
| 3 | 10 |
| 4 | 0,8 |
| 5 | 2 |
| 6 | 3 |
| 7 | 0,28 |
| 8 | 24 |
| 9 | 32 |
| 10 | 164 |
| 11 | 4000 |
| 12 | 0,5 |
| 13 | 10 |
| 14 | 96 |
| 15 | 4 |
| 16 | 40 |
| 17 | 27 |
| 18 | 262 |
| 19 | 125 |
| 20 | 108 |
Решения и критерии оценивания заданий с развёрнутым ответом
| 21 |
В кубе 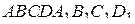 все рёбра равны 4. На его ребре
все рёбра равны 4. На его ребре  отмечена
отмечена
точка 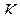 так, что
так, что  . Через точки
. Через точки 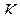 и
и  проведена плоскость
проведена плоскость 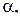 параллельная прямой
параллельная прямой 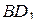 .
.
а) Докажите, что 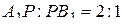 , где
, где  — точка пересечения плоскости
— точка пересечения плоскости 
с ребром  .
.
б) Найдите угол наклона плоскости  к плоскости грани
к плоскости грани 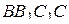 .
.
Решение.
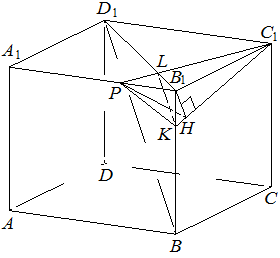
|
а) Проведём через точку  прямую, параллельную
прямую, параллельную 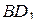 . Пусть эта прямая пересекает плоскость грани
. Пусть эта прямая пересекает плоскость грани 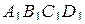 в точке
в точке 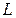 . Прямая
. Прямая 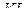 лежит
лежит
в плоскости 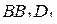 , значит, точка
, значит, точка 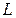 лежит на диагонали
лежит на диагонали  . Более того,
. Более того, 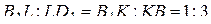 .
.
Прямая 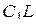 пересекает ребро
пересекает ребро 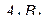
в точке  , принадлежащей плоскости
, принадлежащей плоскости  . Треугольники
. Треугольники 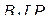 и
и 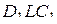 подобны, поэтому
подобны, поэтому 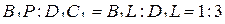 . Значит,
. Значит, 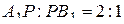 .
.
б) Опустим из точки 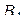 перпендикуляр
перпендикуляр 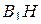 на
на 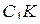 . По теореме о трёх перпендикулярах прямые
. По теореме о трёх перпендикулярах прямые 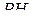 и
и 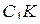 перпендикулярны. Значит, угол
перпендикулярны. Значит, угол  искомый. Поскольку
искомый. Поскольку 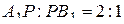 , получаем
, получаем 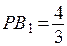 . В прямоугольном треугольнике
. В прямоугольном треугольнике 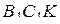 :
:
 .
.
Значит, 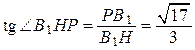 .
.
Ответ: б) 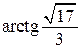 .
.
| 22 |
В правильной треугольной пирамиде 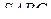 сторона основания
сторона основания 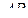 равна 60,
равна 60,
а боковое ребро 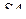 равно 37. Точки
равно 37. Точки 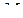 и
и  — середины рёбер
— середины рёбер 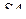 и
и 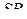 соответственно. Плоскость
соответственно. Плоскость 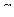 содержит прямую
содержит прямую 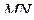 и перпендикулярна плоскости основания пирамиды.
и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость 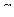 делит медиану
делит медиану 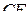 основания в отношении
основания в отношении 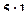 , считая от точки
, считая от точки 
|
|
|
б) Найдите расстояние от вершины  до плоскости
до плоскости 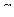 .
.
Решение.

|
а) Прямая 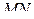 параллельна плоскости
параллельна плоскости 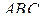 , поэтому сечение пересекает плоскость
, поэтому сечение пересекает плоскость 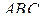 по прямой
по прямой 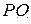 , параллельной
, параллельной 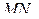 Рассмотрим плоскость
Рассмотрим плоскость 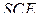 Пусть
Пусть 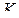 — точка пересечения этой плоскости и прямой
— точка пересечения этой плоскости и прямой 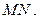
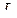 — точка пересечения этой плоскости и прямой
— точка пересечения этой плоскости и прямой 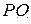 ,
, 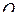 — центр основания пирамиды. Плоскости
— центр основания пирамиды. Плоскости  и
и  перпендикулярны плоскости
перпендикулярны плоскости 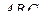 поэтому прямая
поэтому прямая 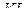 перпендикулярна плоскости
перпендикулярна плоскости 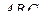 а значит, параллельна прямой
а значит, параллельна прямой 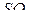 Поскольку
Поскольку 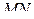 — средняя линия треугольника
— средняя линия треугольника  точка
точка 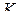 является серединой
является серединой  Следовательно,
Следовательно, 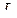 — середина
— середина 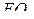 Медиана
Медиана 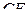 треугольника
треугольника 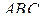 делится точкой
делится точкой 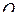 в отношении
в отношении  . Значит,
. Значит,  .
.
б) Прямая 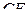 перпендикулярна
перпендикулярна 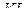 и
и 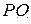 , поэтому прямая
, поэтому прямая 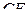 перпендикулярна плоскости
перпендикулярна плоскости  . Прямые
. Прямые 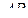 и
и 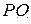 параллельны, значит, расстояние от вершины
параллельны, значит, расстояние от вершины  до плоскости сечения равно расстоянию
до плоскости сечения равно расстоянию
от точки 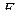 до плоскости сечения, то есть
до плоскости сечения, то есть 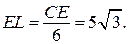
Ответ: б) 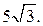
| 23 |
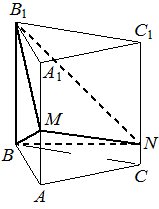
Основанием прямой треугольной призмы 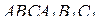 является равнобедренный прямоугольный треугольник
является равнобедренный прямоугольный треугольник 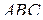 с прямым углом
с прямым углом 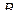 , катеты которого равны 6. Боковые рёбра призмы равны 6. На рёбрах
, катеты которого равны 6. Боковые рёбра призмы равны 6. На рёбрах 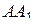
и  отмечены точки
отмечены точки 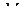 и
и 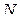 соответственно, причём
соответственно, причём 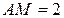 ,
, 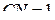 .
.
а) Докажите, что плоскость 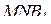 разбивает призму на два многогранника, объёмы которых равны.
разбивает призму на два многогранника, объёмы которых равны.
|
|
|
б) Найдите объём тетраэдра  .
.
Решение.
|
а) Площадь основания призмы равна 18, а объём призмы равен 108.
В четырёхугольной пирамиде 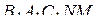 высота совпадает с высотой основания призмы
высота совпадает с высотой основания призмы 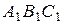 , опущенной на сторону
, опущенной на сторону  , и равна
, и равна 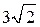 .
.
Основание 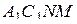 пирамиды
пирамиды 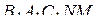 является трапецией, площадь которой равна
является трапецией, площадь которой равна 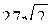 . Значит, объём пирамиды
. Значит, объём пирамиды 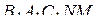 равен 54, то есть составляет половину объёма призмы. Поэтому объёмы многогранников
равен 54, то есть составляет половину объёма призмы. Поэтому объёмы многогранников 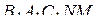 и
и  равны.
равны.
б) В четырёхугольной пирамиде 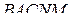 высота совпадает с высотой основания призмы
высота совпадает с высотой основания призмы 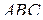 , опущенной на сторону
, опущенной на сторону 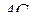 , и равна
, и равна 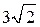 . Основание пирамиды
. Основание пирамиды  является трапецией, площадь которой
является трапецией, площадь которой
равна 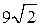 . Объём пирамиды
. Объём пирамиды  равен 18.
равен 18.
Многогранник  состоит из двух частей:
состоит из двух частей:  и
и  . Значит, объём тетраэдра
. Значит, объём тетраэдра  равен 36.
равен 36.
Ответ: б) 36.
| 24 |
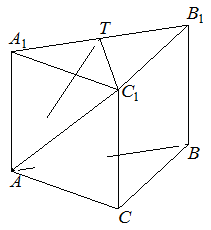
Дана правильная треугольная призма 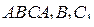 , все рёбра которой равны 4. Точка
, все рёбра которой равны 4. Точка 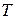 — середина ребра
— середина ребра 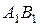 .
.
а) Докажите, что сечение призмы плоскостью 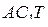 является прямоугольным треугольником.
является прямоугольным треугольником.
б) Найдите угол между плоскостями 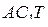 и
и 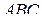 .
.
Решение.
|
а) Найдём стороны треугольника 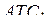 :
:
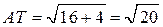 ,
,
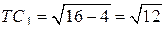 ,
,
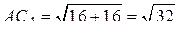 .
.
Заметим, что
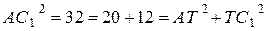 .
.
Следовательно, по теореме, обратной теореме Пифагора, треугольник 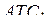 является прямоугольным.
является прямоугольным.
б) Так как прямая  перпендикулярна прямым
перпендикулярна прямым  и
и 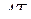 , угол
, угол 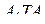 искомый:
искомый:
|
|
|
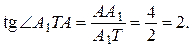
Ответ: б)  .
.
| 25 |
Ребро куба 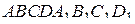 равно 6. Точки
равно 6. Точки 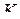 ,
,  и
и 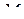 — центры
— центры
граней 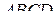 ,
, 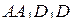 и
и 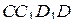 соответственно.
соответственно.
а) Докажите, что 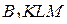 — правильная пирамида.
— правильная пирамида.
б) Найдите объём пирамиды 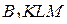 .
.
Решение.
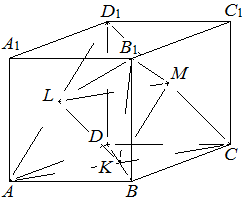
|
а) Рассмотрим правильный тетраэдр  . В нём
. В нём 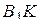 ,
, 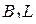 и
и 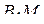 — медианы боковых граней. Значит,
— медианы боковых граней. Значит, 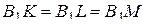 .
.
Основание  пирамиды
пирамиды 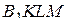 является правильным треугольником, поскольку
является правильным треугольником, поскольку 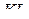 ,
, 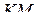 и
и  — средние линии в правильном треугольнике
— средние линии в правильном треугольнике 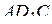 .
.
Таким образом, 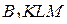 — правильная пирамида.
— правильная пирамида.
б) Объём пирамиды 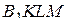 равен четверти объёма пирамиды
равен четверти объёма пирамиды  , поскольку площади треугольников
, поскольку площади треугольников  и
и 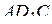 относятся как
относятся как  ,
,
а высота, проведённая из вершины 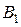 , — общая для этих пирамид.
, — общая для этих пирамид.
С другой стороны, куб 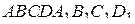 составлен из пирамид
составлен из пирамид  ,
, 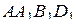 ,
, 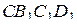 ,
, 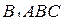 и
и 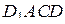 . Пусть объём куба равен
. Пусть объём куба равен 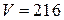 . Тогда объём каждой из пирамид
. Тогда объём каждой из пирамид 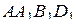 ,
, 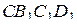 ,
, 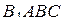
и 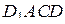 равен
равен 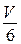 . Значит, объём пирамиды
. Значит, объём пирамиды  равен
равен 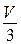 , а объём
, а объём
пирамиды 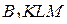 равен
равен  .
.
Ответ: б) 18.
| 26 |
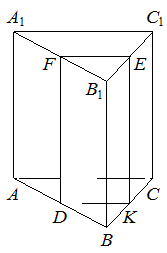
В основании правильной треугольной призмы 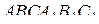 лежит правильный треугольник со стороной 2. Высота призмы равна 3. Точка
лежит правильный треугольник со стороной 2. Высота призмы равна 3. Точка 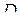 — середина ребра
— середина ребра 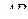 , точка
, точка  — середина ребра
— середина ребра  . Через точки
. Через точки 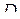 и
и 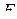 проведена плоскость
проведена плоскость 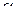 , параллельная ребру
, параллельная ребру  .
.
а) Докажите, что сечение призмы плоскостью 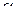 — прямоугольник.
— прямоугольник.
|
|
|
б) Найдите площадь сечения пирамиды плоскостью 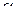 .
.
Решение.
|
а) Обозначим точки пересечения плоскости 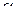
с ребрами 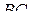 и
и 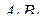 буквами
буквами 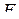 и
и 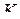 (см. рис.). Плоскость
(см. рис.). Плоскость 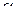 пересекает грани
пересекает грани 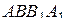 и
и 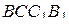
по прямым  и
и 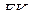 соответственно, параллельным ребру
соответственно, параллельным ребру  . Отрезки
. Отрезки  и
и 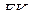 параллельны и равны друг другу. Значит, четырёхугольник
параллельны и равны друг другу. Значит, четырёхугольник  — параллелограмм. Прямая
— параллелограмм. Прямая  перпендикулярна плоскости
перпендикулярна плоскости 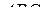 , поэтому прямая
, поэтому прямая  перпендикулярна прямой
перпендикулярна прямой 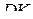 .
.
Следовательно, у параллелограмма  прямые углы, а значит, четырёхугольник
прямые углы, а значит, четырёхугольник 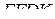 — прямоугольник.
— прямоугольник.
б) Точка 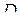 — середина ребра
— середина ребра 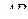 , а точка
, а точка 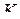 — середина ребра
— середина ребра  . Значит, отрезок
. Значит, отрезок 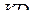 — средняя линия треугольника
— средняя линия треугольника 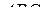 , поэтому
, поэтому 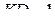 . Поскольку
. Поскольку  , площадь сечения равна
, площадь сечения равна 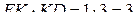 .
.
Ответ: б) 3.
Дата добавления: 2019-09-13; просмотров: 147; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
