Вычисление длины дуги плоской кривой.
Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой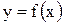 
, где 
.
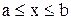Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Если функция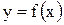 
и ее производная 
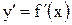непрерывны на отрезке 
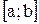, то кривая АВ имеет длину, равную 
.
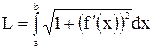Если уравнение прямой АВ задано в параметрической форме
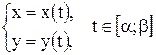, где 
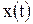и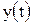 
- непрерывные функции с непрерывными производными и 
, 
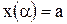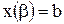, то длина L кривой АВ находится по формуле 
.
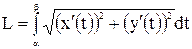Пусть кривая АВ задана уравнением в полярных координатах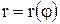 
, 
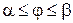. Предположим, что 
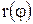и 
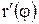непрерывны на отрезке 
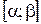, тогда 
.
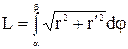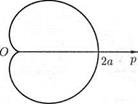
Пример 1. Найти длину кардиоиды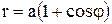 
.
Кардиоида симметрична относительно полярной оси. Найдём половину длины кардиоиды:
Значит, 
.
Вычисление объёма тела.
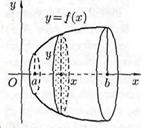Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией 
, отрезком 
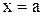и прямыми 
и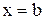 
. Полученная от вращения фигура называется телом вращения.
Формула объёма тела вращения имеет вид: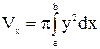 
.
Если криволинейная трапеция ограничена графиком непрерывной функции 
и прямыми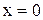 
, 
, 
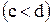., то объём тела, образованного вращением этой трапеции вокруг оси Оу равен: 
.
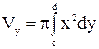Вычисление площади поверхности вращения.
Пусть кривая АВ является графиком функции , где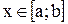 
, а функция 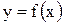и ее производная 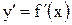непрерывны на этом отрезке. Тогда площадь поверхности S, образованной вращением кривой АВ вокруг оси Ох, находим по формуле: 
.
|
|
|
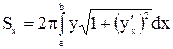Если кривая АВ задана параметрическими уравнениями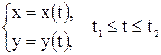 
, то формула для площади поверхности вращения принимает вид: 
.
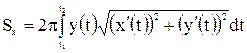Пример 1. Дана циклоида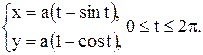 
Найти площадь поверхности, образованной вращением её вокруг оси Ох.
При вращении половины дуги циклоиды вокруг оси Ох площадь поверхности вращения равна
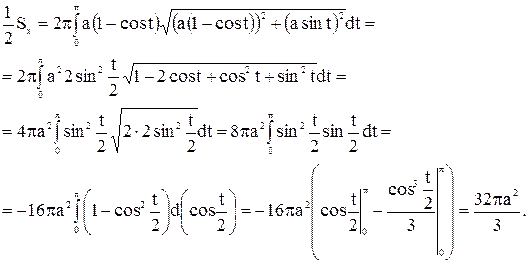
Следовательно,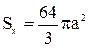 
.
Работа переменной силы.
Пусть материальная точка перемещается из точки а оси Ох в точку b этой оси под действием силы F, параллельной оси Ох. Будем считать, что эта сила является функцией от х, определённой на сегменте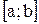 
. Пусть Т – разбиение сегмента 
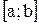точками 
. Выберем на каждом частичном сегменте 
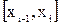точку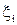 
и будем считать приближённым значением работы А переменной силы 
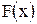на сегменте 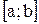выражение 
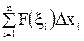. Согласуясь с этими предварительными рассуждениями, мы определим работу А переменной силы 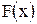на сегменте 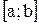как интеграл 
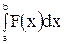. Таким образом,
.
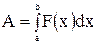Дата добавления: 2019-09-02; просмотров: 201; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!