Основные свойства определенного интеграла
Лекция 4. Определённый интеграл.
Определённый интеграл.
Интегральные суммы. Интегрируемость.
Пусть функция 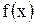 задана на сегменте
задана на сегменте 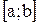 ,
, 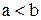 . Обозначим символом Т разбиение сегмента
. Обозначим символом Т разбиение сегмента 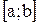 при помощи некоторых, не совпадающих друг с другом точек
при помощи некоторых, не совпадающих друг с другом точек  на
на 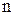 частичных сегментов
частичных сегментов 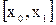 ,
,  [x0, x1], . . .,
[x0, x1], . . ., 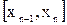 . Точки
. Точки 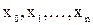 будем называть точками разбиения T. Пусть
будем называть точками разбиения T. Пусть 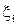 - произвольная точка частичного сегмента
- произвольная точка частичного сегмента 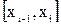 ,
, 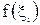 - значение функции в ней. Обозначим через
- значение функции в ней. Обозначим через 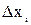 - разность
- разность 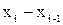 ,которую мы в дальнейшем будем называть длиной частичного сегмента
,которую мы в дальнейшем будем называть длиной частичного сегмента 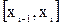 .
.
Определение 1. Число  , где
, где
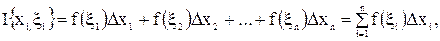
называется интегральной суммой функции 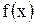 , соответствующей данному разбиению Т сегмента
, соответствующей данному разбиению Т сегмента 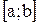 и данному выбору промежуточных точек
и данному выбору промежуточных точек 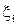 на частичных сегментах
на частичных сегментах 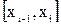 .
.
В дальнейшем через D мы будем обозначать длину максимального частичного сегмента разбиенияТ, то есть 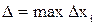 .
.
Выясним геометрический смысл интегральной суммы. Для этого рассмотрим криволинейную трапецию, т. е. фигуру, ограниченную графиком функции 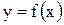 (для простоты будем считать эту функцию непрерывной), двумя ординатами, проведенными в точках а и b оси абсцисс, и осью абсцисс (рис. 1). Очевидно, интегральная сумма
(для простоты будем считать эту функцию непрерывной), двумя ординатами, проведенными в точках а и b оси абсцисс, и осью абсцисс (рис. 1). Очевидно, интегральная сумма  представляет собой площадь ступенчатой фигуры, заштрихованной на рис. 1.
представляет собой площадь ступенчатой фигуры, заштрихованной на рис. 1.
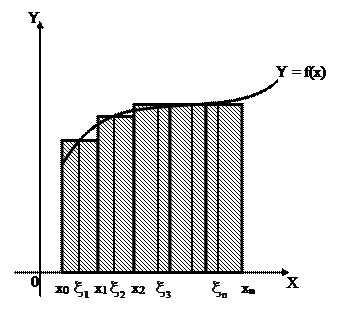
Рис. 1
Определение 2. Число I называется пределом интегральных сумм 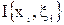 при
при 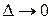 , если для любого положительного числа e можно указать такое положительное число d, что при
, если для любого положительного числа e можно указать такое положительное число d, что при 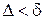 независимо от выбора точек
независимо от выбора точек 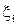 на сегментах
на сегментах 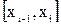 выполняется неравенство
выполняется неравенство
|
|
|
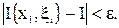
Для предела I интегральных сумм употребляется обозначение
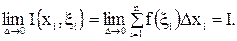
Определение 3. Функция 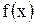 называется интегриру емой на сегменте
называется интегриру емой на сегменте 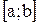 , если существует конечный предел I интегральных сумм этой функции при
, если существует конечный предел I интегральных сумм этой функции при 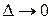 . Указанный предел I называется определенным интегралом от функции
. Указанный предел I называется определенным интегралом от функции 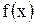 по сегменту
по сегменту 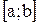 и обозначается следующим образом:
и обозначается следующим образом:
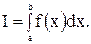
Наглядные геометрические представления показывают, что определенный интеграл численно равен площади криволинейной трапеции, определяемой графиком функции 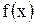 на сегменте
на сегменте 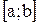 .
.
Выясним вопрос об интегрируемости неограниченных на сегменте [а, b] функций.
Докажем следующее утверждение: неограниченная на сегменте 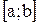 функция
функция 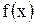 не интегрируема на этом сегменте.
не интегрируема на этом сегменте.
Доказательство. Пусть функция 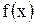 не ограничена на сегменте
не ограничена на сегменте 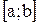 . Тогда она не ограничена на некотором частичном сегменте
. Тогда она не ограничена на некотором частичном сегменте 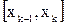 любого данного разбиения Т сегмента
любого данного разбиения Т сегмента 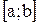 . Поэтому слагаемое
. Поэтому слагаемое  интегральной суммы
интегральной суммы  , отвечающей этому разбиению Т, может быть сделано как угодно большим по абсолютной величине за счет выбора точки
, отвечающей этому разбиению Т, может быть сделано как угодно большим по абсолютной величине за счет выбора точки 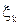 . Отсюда вытекает, что интегральные суммы
. Отсюда вытекает, что интегральные суммы  , отвечающие любому разбиению T, не ограничены и поэтому не существует конечного предела интегральных сумм.
, отвечающие любому разбиению T, не ограничены и поэтому не существует конечного предела интегральных сумм.
|
|
|
Сообразуясь с доказанным утверждением, будем рассматривать лишь ограниченные на сегменте 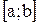 функции. Возникает вопрос: всякая ли ограниченная на сегменте
функции. Возникает вопрос: всякая ли ограниченная на сегменте 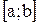 функция является интегрируемой на этом сегменте? Следующий пример показывает, что это, вообще говоря, не так. Убедимся, что заведомо ограниченная на сегменте
функция является интегрируемой на этом сегменте? Следующий пример показывает, что это, вообще говоря, не так. Убедимся, что заведомо ограниченная на сегменте 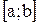 функция Дирихле, значения которой в рациональных точках равны единице, а в иррациональных - нулю, не интегрируема на сегменте
функция Дирихле, значения которой в рациональных точках равны единице, а в иррациональных - нулю, не интегрируема на сегменте 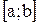 . Действительно, если для любого разбиения Т со сколь угодно малым D выбрать точки
. Действительно, если для любого разбиения Т со сколь угодно малым D выбрать точки 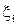 рациональными, то, очевидно,
рациональными, то, очевидно, 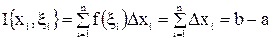 , если же для того же разбиения Т точки
, если же для того же разбиения Т точки 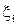 выбрать иррациональными, то
выбрать иррациональными, то 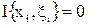 . Поэтому для функции Дирихле не существует предела интегральных сумм, т. е. эта функция не интегрируема.
. Поэтому для функции Дирихле не существует предела интегральных сумм, т. е. эта функция не интегрируема.
Числа  и
и 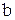 называются нижним и верхним пределами интегрирования,
называются нижним и верхним пределами интегрирования, 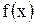 - подынтегральной функцией,
- подынтегральной функцией, 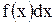 - подынтегральным выражением,
- подынтегральным выражением, 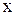 - переменной интегрирования, отрезок
- переменной интегрирования, отрезок 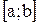 - областью интегрирования.
- областью интегрирования.
Функция 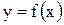 , для которой на отрезке
, для которой на отрезке 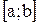 существует определённый интеграл
существует определённый интеграл 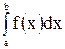 , называется интегрируемой на этом отрезке.
, называется интегрируемой на этом отрезке.
Сформулируем теперь теорему существования определенного интеграла.
|
|
|
Теорема 1 (Коши). Если функция 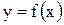 непрерывна на отрезке
непрерывна на отрезке 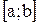 , то определенный интеграл
, то определенный интеграл 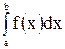 существует.
существует.
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Основные свойства определенного интеграла
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения.
Определенный интеграл не зависит от обозначения переменной интегрирования: 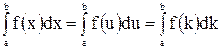 .
.
Эго следует из того, что интегральная сумма, а, следовательно, и ее предел не зависят от того, какой буквой обозначается аргумент данной функции.
Докажем справедливость следующих свойств определенного интеграла:
1°. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
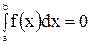 . (1)
. (1)
Отметим, что формула (1) должна рассматриваться как соглашение. Её нужно рассматривать как естественное распространение понятия определенного интеграла на сегмент нулевой длины.
2°. Мы будем считать, что при a < b
|
|
|
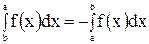 . (2)
. (2)
Эта формула также должна рассматриваться как соглашение. Она представляет собой естественное обобщение понятия интеграла на случай, когда сегмент 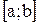 при
при 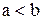 пробегается в направлении от b к а (в этом случае в интегральной сумме все разности
пробегается в направлении от b к а (в этом случае в интегральной сумме все разности 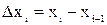 имеют отрицательный знак).
имеют отрицательный знак).
3°. Пусть функции 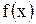 и
и 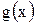 интегрируемы на сегменте
интегрируемы на сегменте 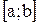 . Тогда функции
. Тогда функции 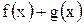 ,
, 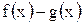 ,
, 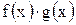 также интегрируемы на этом сегменте, причем
также интегрируемы на этом сегменте, причем
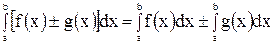 . (3)
. (3)
Докажем сначала интегрируемость функции 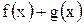 и справедливость формулы (3). При любом разбиении сегмента
и справедливость формулы (3). При любом разбиении сегмента 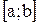 и любом выборе точек
и любом выборе точек 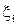 для интегральных сумм справедливо соотношение
для интегральных сумм справедливо соотношение
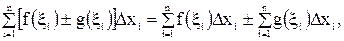
а поэтому из существования предела правой части следует существование предела левой части. Следовательно, функция 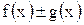 интегрируема и имеет место формула (3).
интегрируема и имеет место формула (3).
4°. Если функция 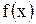 интегрируема на сегменте
интегрируема на сегменте 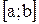 , то функция
, то функция 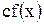
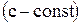 интегрируема на этом сегменте, причем
интегрируема на этом сегменте, причем
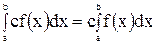 . (4)
. (4)
Действительно, интегральные суммы функций 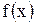 и
и 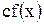 отличаются постоянным множителем с. Поэтому функция
отличаются постоянным множителем с. Поэтому функция  интегрируема и справедлива формула (4).
интегрируема и справедлива формула (4).
5°. Пусть функция 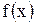 интегрируема на сегменте
интегрируема на сегменте 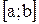 . Тогда эта функция интегрируема на любом сегменте
. Тогда эта функция интегрируема на любом сегменте 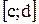 , содержащемся в сегменте
, содержащемся в сегменте  .
.
6°. Пусть функция 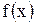 интегрируема на сегментах
интегрируема на сегментах 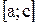 и
и 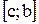 . Тогда эта функция интегрируема на сегменте
. Тогда эта функция интегрируема на сегменте  , причем
, причем
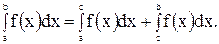 (5)
(5)
То есть интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определённого интеграла.
Если точка с лежит вне сегмента  , то сегмент
, то сегмент  есть часть сегмента
есть часть сегмента 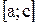 (или
(или 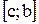 ) и поэтому, в силу свойства 5°, функция f(x) интегрируема на
) и поэтому, в силу свойства 5°, функция f(x) интегрируема на 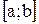 . Рассмотрим случай a < b < c. Тогда
. Рассмотрим случай a < b < c. Тогда
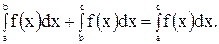
7°. «Теорема о среднем». Если функция  непрерывна на отрезке
непрерывна на отрезке 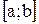 , то существует точка
, то существует точка 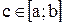 , такая что
, такая что 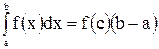 .
.
Данное свойство при 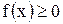 имеет простой геометрический смысл: значение определённого интеграла равно, при некотором
имеет простой геометрический смысл: значение определённого интеграла равно, при некотором 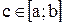 площади прямоугольника с высотой
площади прямоугольника с высотой 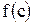 и основанием
и основанием 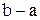 . Число
. Число 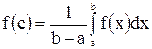 - называется средним значением функции
- называется средним значением функции  на отрезке
на отрезке  .
.
9°. Если функция  сохраняет знак на отрезке
сохраняет знак на отрезке  , где
, где 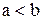 , то интеграл
, то интеграл  имеет тот же знак, что и функция. Так, если
имеет тот же знак, что и функция. Так, если  на отрезке
на отрезке 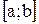 , то
, то 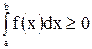 .
.
9°. Неравенство между непрерывными функциями на отрезке 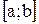 ,
, 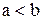 можно интегрировать. Так, если
можно интегрировать. Так, если 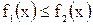 при
при 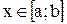 , то
, то 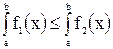 .
.
10°. Оценка интеграла. Если m и M - соответственно наименьшее и наибольшее значения функции 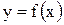 на отрезка
на отрезка  , (
, ( 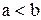 ), то
), то 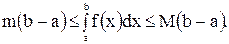
 Если
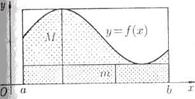
Если  , то свойство 9° иллюстрируется геометрически: площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть
, то свойство 9° иллюстрируется геометрически: площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть 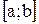 , а высоты равны m и M (рис. 2).
, а высоты равны m и M (рис. 2).
11°. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции: 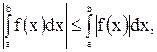
 .
.
Дата добавления: 2019-09-02; просмотров: 175; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
