Лекция 18. Экстремум функции двух переменных.
Основные вопросы:
1. Основные понятия.
2. Необходимое и достаточное условия существования экстремума.
3. Наибольшее и наименьшее значение функции в замкнутой области.
Обзор лекции:
В данной лекции рассматриваются понятие экстремума функции двух переменных; необходимое и достаточное условия существования экстремума, алгоритмом нахождения экстремума функции двух переменных, наибольшее и наименьшее значение функции в замкнутой области.
- Основные понятия.
Пусть функция z=f(x;у) определена на множестве D и точка М 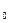 (х
(х 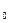 ;у
;у 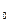 )
) 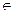 D. Если существует окрестность точки М
D. Если существует окрестность точки М 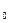 , которая принадлежит множеству D, и для всех отличных от М
, которая принадлежит множеству D, и для всех отличных от М 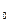 точек М выполняется неравенство
точек М выполняется неравенство
f(М)< f(М0) (f(М)> f(М0)),
то точку М 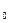 называют точкой локального максимума (минимума) функции z=f(x;у), а число f(М0) - локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
называют точкой локального максимума (минимума) функции z=f(x;у), а число f(М0) - локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
2. Необходимое и достаточное условия существования экстремума.
Теорема 1(необходимые условия экстремума). Если функция z=f(x;у) в точке
М  ( х
( х  ;у
;у  ) имеет локальный экстремум, то в этой точке частные производные
) имеет локальный экстремум, то в этой точке частные производные  равны нулю или не существуют.
равны нулю или не существуют. 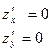
Точки, в которых 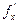 =
= 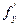 = 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
= 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
Пусть в стационарной точке М  ( х
( х  ;у
;у  ) и некоторой её окрестности функция z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:
) и некоторой её окрестности функция z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:
|
|
|
А=  ( х
( х  ;у
;у  ), В=
), В= 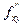 ( х
( х  ;у
;у  ), С=
), С= 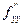 ( х
( х  ;у
;у  ),
), 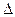 =АС-В2.
=АС-В2.
Теорема 2 (достаточные условия экстремума).
1. Если 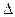 >0, то функция z=f(x;у) в точке М
>0, то функция z=f(x;у) в точке М  имеет экстремум, причём максимум при А<0 и минимум при А>0.
имеет экстремум, причём максимум при А<0 и минимум при А>0.
2. Если 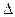 <0, то в точке М
<0, то в точке М  нет экстремума.
нет экстремума.
3. Если 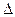 =0, то вопрос о наличии экстремума остается открытым.
=0, то вопрос о наличии экстремума остается открытым.
Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:
1°. Найти частные производные функции  и
и 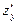
2°. Решить систему уравнений  =0,
=0, 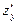 =0 и найти критические точки функции.
=0 и найти критические точки функции.
3°. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
4°. Найти экстремумы(экстремальные значения) функции.
3. Наибольшее и наименьшее значение функции в замкнутой области.
Пусть в замкнутой и ограниченной области D задана непрерывная функция z=f(x;у). По теореме Вейершрасса функция достигает своего наименьшего и наибольшего значения.
Теорема (свойство непрерывных функций в замкнутой и ограниченной области). Если функция z=f(x;у) непрерывна в замкнутой и ограниченной области, то в этой области существуют такие точки, в которых функция достигает своего наименьшего и наибольшего значения.
|
|
|
Пусть функция u = f ( x1 , x2 ,…, xn) определена и непрерывна в некотором ограниченном и замкнутом множестве D и имеет на этом множестве конечные частные производные (за исключением, быть может, отдельных точек). Тогда эта функция достигает на D своего наибольшего и наименьшего значения. Если это значение достигается во внутренней точке множества, то, очевидно, эта точка должна быть стационарной; кроме того, наибольшее и наименьшее значение может достигаться на границе множества D. Поэтому для определения наибольшего и наименьшего значений функции на множестве D требуется:
1) найти стационарные точки функции, принадлежащие D, и вычислить значения функции в этих точках;
2) найти наибольшее и наименьшее значение, принимаемое функцией на границе множества D;
3) выбрать наименьшее и наибольшее из полученных чисел, которые и будут являться наименьшим и наибольшим значениями функции на всем множестве D.
Контрольные вопросы:
- Сформулируйте определение локального экстремума функции двух переменных
- Сформулируйте необходимое и достаточное условие экстремума функции двух переменных.
- Алгоритм исследования функции двух переменных на наличие экстремума
- Алгоритм нахождения наибольшего и наименьшего значения функции двух переменных в замкнутой области
|
|
|
Тесты
Числовые последовательности. Предел последовательности
1. Последовательность 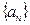 , заданная формулой
, заданная формулой  го члена
го члена 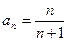 является:
является:
а) возрастающей; б) убывающей; в) неограниченной; г) невозрастающей.
2. Последовательность 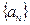 , заданная формулой
, заданная формулой  го члена
го члена  является:
является:
а) возрастающей; б) неубывающей; в) неограниченной; г) ограниченной.
3. Предел последовательности 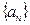 , заданной формулой
, заданной формулой  го члена
го члена 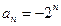 равен:
равен:
а) 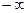 ; б)
; б) 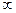 ; в) 0; г) -2.
; в) 0; г) -2.
4. Предел последовательности 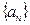 , заданной формулой
, заданной формулой  го члена
го члена 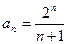 равен:
равен:
а) 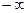 ; б)
; б) 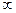 ; в) 0; г) -2.
; в) 0; г) -2.
5. Предел последовательности 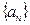 , заданной формулой
, заданной формулой  го члена
го члена 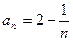 равен:
равен:
а) 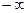 ; б)
; б) 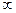 ; в) 0; г) 2.
; в) 0; г) 2.
6. Предел последовательности 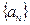 , заданной формулой
, заданной формулой  го члена
го члена  равен:
равен:
а) 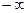 ; б)
; б) 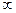 ; в) 0; г) 2.
; в) 0; г) 2.
7. Предел последовательности 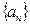 , заданной формулой
, заданной формулой  го члена
го члена 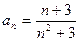 равен:
равен:
а) 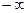 ; б)
; б) 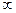 ; в) 0; г) 2.
; в) 0; г) 2.
8. Среди перечисленных вариантов ответов выбрать значение предела 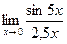 :
:
а) 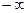 ; б) 2; в) 3; г) 0.
; б) 2; в) 3; г) 0.
9. Среди перечисленных вариантов ответов выбрать значение предела 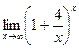 :
:
а) 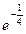 ; б)
; б)  ; в)
; в) 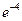 ; г)
; г) 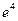 .
.
10. Среди перечисленных вариантов ответов выбрать значение предела 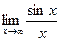 :
:
|
|
|
а) 1; б) 0; в) 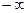 ; г)
; г) 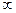 .
.
Функция одной переменной
11. Указать числовой промежуток, на котором определена функция  :
:
а)  ; б)
; б)  ; в)
; в) 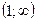 ; г)
; г) 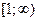 .
.
12. Указать числовой промежуток, на котором определена функция 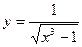 :
:
а) 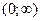 ; б)
; б)  ; в)
; в) 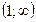 ; г)
; г) 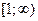 .
.
13. Указать числовой промежуток, на котором определена функция 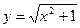 :
:
а) 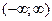 ; б)
; б)  ; в)
; в) 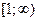 .
.
14. Какова область значений функции 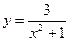 :
:
а) 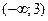 ; б)
; б) 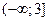 ; в)
; в) 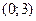 ; г)
; г) 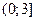 .
.
15. Какова область значений функции  :
:
а) 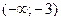 ; б)
; б) 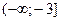 ; в)
; в) 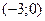 ; г)
; г) 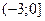 .
.
16. Какова область значений функции 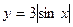 :
:
а) 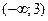 ; б)
; б) 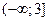 ; в)
; в)  ; г)
; г)  .
.
17. Какое из перечисленных свойств относится к функции  :
:
а) функция является чётной; б) функция является нечётной; в) функция является функцией общего вида; г) функция является периодической.
18. Какое из перечисленных свойств относится к функции 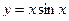 :
:
а) функция является чётной; б) функция является нечётной; в) функция является функцией общего вида; г) функция является периодической.
19. Какая из перечисленных функций является обратной для функции 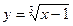 на промежутке
на промежутке 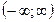 :
:
а) 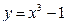 ; б)
; б) 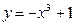 ; в)
; в) 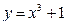 ; г)
; г) 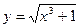 .
.
20. Какая из перечисленных линий является графиком функции 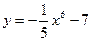 :
:
а) кубическая парабола; б) квадратичная парабола; в) гипербола; г) экспонента.
21. Какая из перечисленных линий является графиком функции 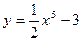 :
:
а) кубическая парабола; б) квадратичная парабола; в) гипербола; г) экспонента.
22. Какое из перечисленных утверждений истинно? Функция  на всей области определения является:
на всей области определения является:
а) неубывающей; б) невозрастающей; в) неотрицательной; г) неположительной.
Пределы функций
23.  Указать ВСЕ утверждения, справедливые для графика функции, изображенного на рис.:
Указать ВСЕ утверждения, справедливые для графика функции, изображенного на рис.:
| а) | 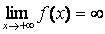
| б) | 
| в) | 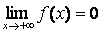
|
| г) | 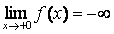
| д) | 
| е) | 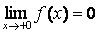
|
24. Значение предела 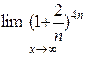 равно:
равно:
А) 1 Б) е8 В) 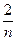 Г) е4
Г) е4
25. Вычислить предел 
А) ∞ Б) 2 В) - ∞ Г) 1
26. Вычислить 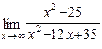
А) 35 Б) 12 В) ∞ Г) 1
27. Вычислить 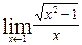
А) 2 Б) 0 В) ∞ Г) 5
Непрерывность функции. Производная функции
28. Для функции  точка
точка  является:
является:
а) точкой непрерывности; б) точкой устранимого разрыва; в) точкой разрыва первого рода (скачка); г) точкой разрыва второго рода (бесконечного).
29. Для функции 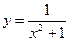 точка
точка  является:
является:
а) точкой непрерывности; б) точкой устранимого разрыва; в) точкой разрыва первого рода (скачка); г) точкой разрыва второго рода (бесконечного).
30. Если функция дифференцируема в точке x 0, то в этой точке функция будет
А) иметь экстремум; Б) иметь производную; В) непрерывна; Г) Другой ответ.
31. Какое из ниже перечисленных предложений определяет производную функции (когда приращение аргумента стремится к нулю)?
а) Отношение приращения функции к приращению аргумента; б) Предел отношения функции к приращению аргумента; в) Отношение функции к пределу аргумента; г) Отношение предела функции к аргументу; д) Предел отношения приращения функции к приращению аргумента.
32. Первая производная функции показывает
а) скорость изменения функции; б) направление функции; в) приращение функции;
г) приращение аргумента функции.
33. Угловой коэффициент касательной, проведенной к графику функции в некоторой точке, равен
а) отношению значения функции к значению аргумента в этой точке; б) значению производной функции в этой точке; в) значению дифференциала функции в этой точке; г) значению функции в этой точке; д) значению тангенса производной функции в этой точке.
34.  На рисунке изображен график функции
На рисунке изображен график функции 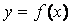 . Тогда производная
. Тогда производная 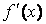 это ...
это ...
а) TK/МК;
б) NK/МК;
в) NК;
г) MK/ТК;
д) MN/МК;
е) MN.
35. Дифференциал функции равен
а) отношению приращения функции к приращению аргумента; б) произведению приращения функции на приращение аргумента; в) произведению производной на приращение аргумента;
г) приращению функции; д) приращению аргумента.
36. Дифференциал постоянной равен…
а) этой постоянной; б) произведению данной постоянной на величину Dx;
в) бесконечно большой величине; г) нулю; д) невозможно определить.
37. На рисунке изображен график функции y=f(x) . Какой отрезок на этом рисунке соответствует дифференциалу dy?
 а) TK;
а) TK;
б) NK;
в) NT;
г) MK;
д) MN;
е) другой ответ.
38. Если функция у(х) непрерывна на [a;b], дифференцируема на (a;b) и y(a) = y(b), то на (a ; b) можно найти хотя бы одну точку, в которой
а) функция не определена; б) производная функции не существует; в) нельзя провести касательную к графику функции; г) производная функции обращается в ноль.
39. Дифференциал функции 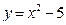 равен
равен
А) d 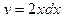 ; Б) d
; Б) d 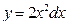 ; В) d
; В) d 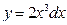 ; Г) Другой ответ.
; Г) Другой ответ.
40. Приближённое значение функции 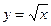 , вычисленное с помощью дифференциала в точке x0=3 равно:
, вычисленное с помощью дифференциала в точке x0=3 равно:
А) 1,9; Б) 1,75; В) 2; Г) Другой ответ.
41. Производная функции 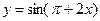 равна
равна
А) 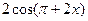 ; Б)
; Б) 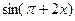 ; В)
; В) 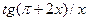 ; Г) Другой ответ.
; Г) Другой ответ.
42. Пусть функция 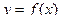 имеет в точке
имеет в точке 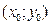 конечную производную. Тогда уравнение касательной к функции в этой точке имеет вид:
конечную производную. Тогда уравнение касательной к функции в этой точке имеет вид:
А) 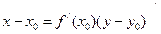 ; Б)
; Б) 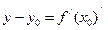 ; В)
; В) 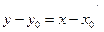 ;
;
Г) 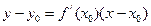 .
.
43. Производная функции  равна:
равна:
А) 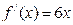 ; Б)
; Б)  ; В)
; В)  ; Г)
; Г) 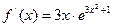 .
.
44. Производная функции 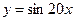 равна
равна
А) 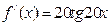 ; Б)
; Б)  ; В)
; В) 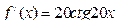 ;
;
45. Найти угловой коэффициент касательной к графику функции 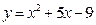 в точке
в точке 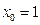 .
.
А) 5 Б) 6 В) 7 Г) 8
46. Найти производную функции  ..
..
А) 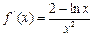 ; Б)
; Б) 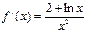 ; В)
; В)  ; Г)
; Г) 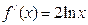 .
.
47. Найти вторую производную функции  в точке
в точке 
А) 16 Б) 17 В) 18 Г) 19
48. Функция у = х3+х …
а) возрастает на ( – ∞; 0), убывает на (0; +∞); б) убывает на ( – ∞; 0), возрастает на (0; +∞);
в) всюду убывает; г) всюду возрастает; д) другой ответ.
49. Сколько точек перегиба имеет функция у = х4 + 4х?
а) ни одной; б) одну; в) две; г) три; д) больше трех.
50. Укажите точки экстремума непрерывной на всей числовой прямой функции у( х), если 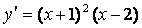 :
:
а) х = 2 – точка max; б) х = 2 – точка min; в) х = –1 – точка max; г) х = –1 – точка min; д) точек экстремума нет.
51. Для дифференцируемой функции f(x) из приведенных условий выберите достаточное условие убывания:
а)  ; б)
; б) 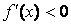 ; в)
; в) 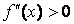 ; г)
; г)  ; д)
; д) 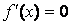
52. Какой из графиков на рисунке соответствует функции y = f(x), удовлетворяющей условиям f '( x ) < 0; f ''( x ) > 0?

53. Для функции, изображенной на рисунке, укажите:

А) точки на (a; b), в которых функция не дифференцируема.
Б) точки, в которых функция имеет максимум.
В) точки на [a; b], в которых функция принимает наименьшее значение.
Г) точки на (a; b) в которых производная функции обращается в ноль.
Заключение
Математический анализ является одной из наиболее значительных частей математики. Характерной чертой этого раздела можно назвать его тесную связь с практикой.
Как и любая математическая дисциплина, математический анализ имеет свой объект исследования и свой метод исследования, опирающийся на первоначальные понятия множества и функции. Объектом исследования в математическом анализе являются функции, их свойства и операции над ними (дифференцирование, интегрирование и другие). Метод исследования — предельный переход.
Дата добавления: 2019-07-15; просмотров: 282; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
