Лекция 8-9. Непрерывность функций

Основные вопросы:

1. Односторонние пределы

Непрерывность функции в точке и на интервале.

3. Точки разрыва функции и их классификация.

4. Кусочно-непрерывные функции

Основные теоремы о непрерывных функциях. Непрерывность элементарных функций.
Свойства функций, непрерывных на отрезке.

Обзор лекции:

В данной лекции рассматриваются односторонние пределы функции, понятие непрерывности функции в точке и на интервале, свойства непрерывных функций, классификация точек разрыва функции, кусочно-непрерывные функции.

1. Односторонние пределы.

Под односторонним пределом числовой функции подразумевают «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) (рис. 1) и правосторонним пределом (пределом справа)

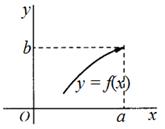
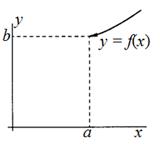
Определение. Число А называется пределом функции у = f(x) при х, стремящемся к х₀ слева (справа), если 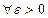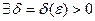такое, что |f(x)-A|<ε при x₀– х < δ (х - х₀< δ).

Обозначения: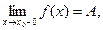

Теорема (второе определение предела). Функция y=f(x) имеет при х, стремящемся к х₀, предел, равный А, в том и только в том случае, если оба ее односторонних предела в этой точке существуют и равны А.

2. Непрерывность функции в точке и на интервале.

Определение. Функция y=f(x) называется непрерывной в точке х₀, если

Замечание. Из этого определения следует, во-первых, что функция определена при х = = х₀, и во-вторых, что при х→х₀ существует конечный предел функции.

Свойства непрерывных функций.

1. Если функции f(x) и g(x) непрерывны при х = х₀, то f(x)+g(x) тоже непрерывна при х = х₀.

2. Если функции f(x) и g(x) непрерывны при х = х₀, то f(x)g(x) тоже непрерывна при х = х₀.

3. Если функции f(x) и g(x) непрерывны при х = х₀, то f(x)/g(x) тоже непрерывна при х = х₀ при условии, что g(x₀) ≠ 0.

4. Если u=φ(x) непрерывна при х = х₀, а f(u) непрерывна при u = u(x₀), то сложная функция f(φ(x)) непрерывна при х = х₀.

3. Точки разрыва и их классификация.

Определение. Пусть функция f(x) определена в некоторой окрестности точки х₀, за исключением, возможно, самой этой точки. Тогда х₀ называется точкой разрыва функции f(x), если она либо не определена при х = х₀, либо не является непрерывной в точке х₀.

Определение. Если существует конечный предел f(x) при х→х₀, но не равный f(x₀), точка разрыва х₀ называется устранимой особенностью.

Замечание. Термин «устранимая особенность» связан с тем, что, доопределив функцию в точке разрыва значением ее предела в этой точке, мы сделаем ее непрерывной при х = х₀, то есть устраним разрыв в рассматриваемой точке.

Определение. Если существуют конечные односторонние пределы f(x) при х→х₀, точка х₀ называется точкой разрыва 1-го рода.

Определение. Все остальные точки разрыва называются точками разрыва 2-го рода.

Примеры.

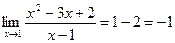1. Функция не определена при х = 1, а для остальных значений аргумента может быть представлена как у = х - 2. Следовательно, , то есть х = 1 – устранимая особенность.

2. 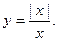Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом 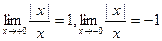. Следовательно, х = 0 –точка разрыва 1-го рода.

3. 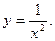Функция не определена при х = 0 , и 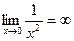. Поэтому х = 0 – точка разрыва 2-го рода.

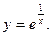
4. 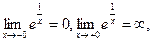то есть правосторонний предел не является конечным. Значит, х = 0 – точка разрыва 2-го рода.

5. 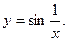Функция не определена при х = 0 и не имеет предела при х→0. Следовательно, х = 0 – точка разрыва 2-го рода.

4.Кусочно-непрерывные функции

Еще раз подчеркнем, что непрерывность функции в любой точке области определения гарантируется лишь для элементарных функций.

Основные теоремы о непрерывных функциях. Непрерывность элементарных функций.

Теорема 1. Сумма конечного числа непрерывных функций является непрерывной функцией.

Пусть функции 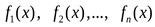непрерывны в точкех₀ и

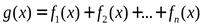Тогда имеем

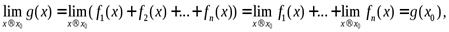ч.т.д.

Теорема 2. Произведение конечного числа непрерывных функций является непрерывной функцией.

Доказательство аналогично.

Теорема 3. Частное двух непрерывных функций является непрерывной функцией, если знаменатель в рассматриваемой точке не равен нулю.

Доказательство аналогично.

Теорема 4. Пусть функция 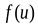непрерывна в точкеи₀, а функция непрерывна в точкех₀ и пусть 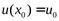. Тогда сложная функция 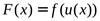непрерывна в точкех₀.

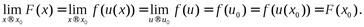
Здесь была использована подстановка 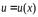и условие непрерыв-ности функции 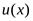в точкех₀.

В результате доказательств этих теорем и непрерывности основных элементарных функций приходим к важной обобщающей теореме:

Теорема 5. Все элементарные функции непрерывны в своей области определения.

Свойства функций, непрерывных на отрезке.

Первая теорема Больцано-Коши. Пусть функция определена и непрерывна на 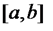, а на концах сегмента принимает значения разных знаков, то есть 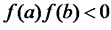Тогда существует такая точка , что .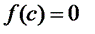

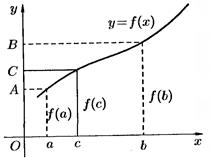
Геометрический смысл: График непрерывной на промежутке и принимающей в двух точках этого промежутка значения разных знаков пересекает ось абсцисс по крайней мере в одной точке: f(a)<0, f(b)>0, f(c)=0.

Теорема (вторая теорема Больцано - Коши) Если функция f непрерывна на [a, b] и в двух его точках a и b: f(a)=A, B=f(b), то для всякой точки с∈[а, b] между точками a и b найдется хотя бы одна точка c, что f(c)=C.

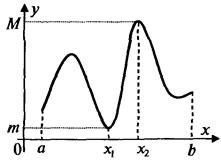
Первая теорема Вейерштрасса (об ограниченности непрерывной функции).

Если функция f непрерывна на [a, b], то она ограничена на нем, т.е. существует такое число M, что |f(x)| ≤ M, при всех x ∈ [a, b].

Теорема (вторая теорема Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на нем свое наибольшее и наименьшее значения.

Контрольные вопросы:

1. Как определяется непрерывность функции в точке?

2. Что такое непрерывная на интервале (отрезке) функция?

3. Каковы основные свойства функций, непрерывных на отрезке?

4. Какая точка называется точкой разрыва функции?

5. Какая точка называется точкой устранимого разрыва функции?

6. Какая точка называется точкой разрыва I рода функции?

7. Какая точка называется точкой разрыва II функции?

Дата добавления: 2019-07-15; просмотров: 223; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!