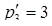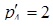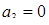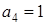Восстановление позиционного представления числа по его остаткам
Система остаточных классов обладает одной особенностью, которую можно отнести к недостаткам этой системы: нельзя визуально определить величину числа, представленного в СОК, а следовательно затруднительно и выполнение таких операций, как сравнение чисел, определение знака числа. Один из путей решения этой проблемы состоит в преобразовании чисел из СОК в позиционную систему счисления. Оценим существующие способы перевода, как традиционные: метод ортогональных базисов; перевод числа в обобщенную позиционную систему (ОПС), так и недавно появившиеся интервальные методы перевода.
1). Метод восстановления числа по его остаткам был найден еще в Китае две тыс. лет назад. Основой этого метода является теорема, названная, поэтому Китайской теоремой об остатках (КТО).
Теорема. Пусть  – попарно взаимно простые числа,
– попарно взаимно простые числа,  =
=  ,
, 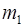 ,
, 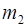 , …,
, …, 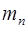 подобраны так, что
подобраны так, что 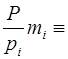 1
1  ,
,  =
= 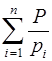
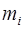
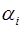 ,
, 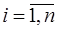 . Тогда решение системы
. Тогда решение системы 
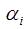
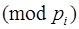 ,
, 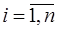 , будет иметь вид:
, будет иметь вид: 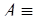

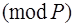 .
.
Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления.
Пусть основания системы остаточных классов 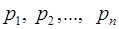 ;
; 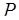 = =
= = 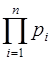 – объем диапазона системы. С выбором системы определяются ее основные константы – базисы
– объем диапазона системы. С выбором системы определяются ее основные константы – базисы  ,
, 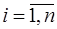 . Задача перевода числа
. Задача перевода числа 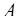 = =(
= =( 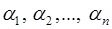 ) в ПСС заключается в определении таких чисел
) в ПСС заключается в определении таких чисел 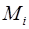 ,
, 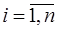 , чтобы
, чтобы 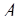 =
= 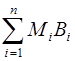 . Для однозначного определения
. Для однозначного определения 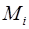 на базисы системы
на базисы системы 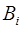 накладывается ряд ограничений и показывается, что таким свойством обладают базисы
накладывается ряд ограничений и показывается, что таким свойством обладают базисы
|
|
|
 = (1, 0, 0, …, 0, 0),
= (1, 0, 0, …, 0, 0), 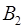 =(0, 1, 0, …, 0, 0),
=(0, 1, 0, …, 0, 0), 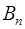 = (0, 0, 0, …, 0, 1),
= (0, 0, 0, …, 0, 1),
которые называются ортогональными.
Тогда в случае ортогональных базисов 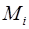 =
= 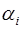 ,
, 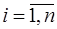 . Ортогональные базисы определяются по формуле
. Ортогональные базисы определяются по формуле
 =
= 
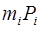 ,
, 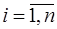 , (3.1´)
, (3.1´)
где
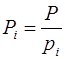 =
= 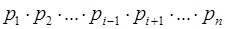 (3.2´)
(3.2´)
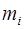 – целые положительные числа, которые называются весами базиса, их определяют из сравнений
– целые положительные числа, которые называются весами базиса, их определяют из сравнений
 º 1
º 1 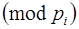 (3.3´)
(3.3´)
Тогда, по Китайской теореме, число
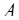 = (
= ( 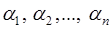 )
)  .
.
Таким образом, если найдены ортогональные базисы для системы оснований, то для перевода числа 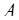 = (
= ( 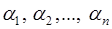 ) достаточно вычислить
) достаточно вычислить 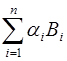 и ввести эту сумму в диапазон [0;
и ввести эту сумму в диапазон [0; 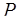 ) вычитанием величины, кратной
) вычитанием величины, кратной 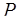 , т.е.
, т.е.
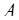 =
= 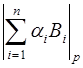 =
= 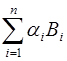 –
– 
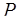 , (3.4´)
, (3.4´)
где  – ранг числа
– ранг числа 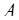 , показывающий сколько раз надо вычесть величину диапазона
, показывающий сколько раз надо вычесть величину диапазона 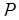 из полученного числа, чтобы вернуть его в диапазон.
из полученного числа, чтобы вернуть его в диапазон.
Пример. Пусть дана система оснований 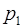 = 2,
= 2,  = 3,
= 3,  = 5,
= 5, 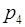 =7,
=7, 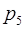 =11, объем диапазона
=11, объем диапазона 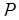 =2·3·5·7·11=2310. перевести число
=2·3·5·7·11=2310. перевести число 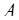 = (1, 2, 1, 4, 7) в позиционную систему.
= (1, 2, 1, 4, 7) в позиционную систему.
Вычислим ортогональные базисы.
Для этого найдем величины  :
:
 =1155,
=1155, 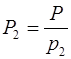 =770,
=770,  =462,
=462, 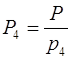 =330,
=330,
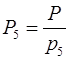 =210.
=210.
Ищем веса базисов:
1155 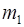 º 1(
º 1( 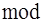 2),
2),  º 1(
º 1( 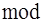 2).
2).
770 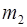 º 1(
º 1( 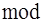 3),
3),  º 2(
º 2( 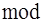 3).
3).
462  º 1(
º 1( 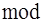 5),
5),  º 3(
º 3( 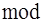 5).
5).
330 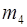 º 1(
º 1( 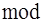 7),
7), 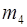 º 1(
º 1( 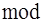 7).
7).
210 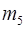 º 1(
º 1( 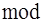 11),
11), 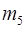 º 1(
º 1( 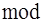 11).
11).
Тогда получаем сами базисы:
|
|
|
 =
= 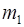 ·
· 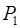 = 1·1155 =1155,
= 1·1155 =1155,
 =
=  ·
· 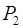 = 2·770 =1540,
= 2·770 =1540,
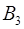 =
= 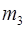 ·
· 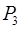 = 3·462 =1386,
= 3·462 =1386,
 =
= 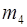 ·
· 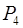 = 1·330 =330,
= 1·330 =330,
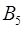 =
= 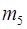 ·
·  = 1·210 =210.
= 1·210 =210.
Вычислим величину числа 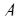 :
:
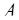 =
=  =
= 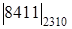 =1481.
=1481.
Так как ортогональные базисы 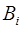 полностью определяются выбором оснований системы, то они могут быть заранее вычислены, причем единственный раз.
полностью определяются выбором оснований системы, то они могут быть заранее вычислены, причем единственный раз.
Недостаток рассмотренного метода заключается в том, что приходится иметь дело с большими числами  и, кроме того, действия сложения и умножения надо выполнять в позиционной системе счисления, а полученный результат необходимо вводить в диапазон вычитанием величины кратной
и, кроме того, действия сложения и умножения надо выполнять в позиционной системе счисления, а полученный результат необходимо вводить в диапазон вычитанием величины кратной 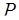 .
.
2). Другой метод определения величины числа связан с переводом числа из системы остаточных классов в ОПС. Для того чтобы рассмотреть этот метод, выявим связь между представлением некоторого числа 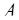 в этих двух системах. Пусть по-прежнему СОК задается основаниями
в этих двух системах. Пусть по-прежнему СОК задается основаниями  и
и  = (
= ( 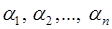 ) – число в этой системе. И пусть
) – число в этой системе. И пусть 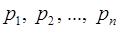 – также основания ОПС, тогда число
– также основания ОПС, тогда число 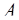 можно представить в виде
можно представить в виде
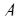 =
= 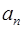
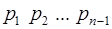 +
+ 
 +…+
+…+
+ 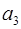
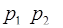 +
+ 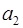
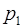 +
+ 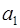 , (3.5´)
, (3.5´)
где 0 £ 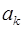 <
< 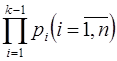 – коэффициенты (цифры) ОПС.
– коэффициенты (цифры) ОПС.
Очевидно, что диапазоны чисел, представимых в СОК и ОПС совпадают, т.е. можно говорить о наличии взаимооднозначного соответствия между множеством представлений чисел в СОК и ОПС.
Равенство (3.5´) можно переписать в виде
|
|
|
 =
= 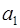 +
+ 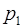 (
( 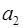 +
+  (
( 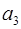 +…+
+…+ 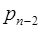 (
(  +
+ 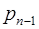
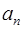 )…)),
)…)),
откуда следует, что цифры ОПС могут быть получены из соотношений:
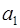 =
= 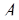 –
– 
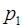 =
= 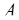 –
– 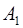
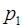 , где
, где 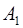 =
=  ,
,
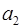 =
=  –
– 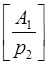
 =
= 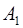 –
– 
 , где
, где  =
= 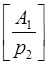 , (3.6´)
, (3.6´)
…
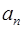 =
= 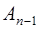 –
– 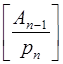
 =
= 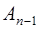 –
– 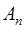
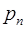 , где
, где 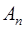 =
= 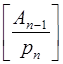 .
.
Причем при определении цифр 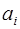 по формулам (3.6´) все вычисления можно вести в СОК.
по формулам (3.6´) все вычисления можно вести в СОК.
Действительно, из (3.6´) следует, что 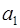 =
=  , т.е.
, т.е. 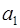 – первая СОК цифра или
– первая СОК цифра или 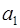 =
= 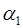 . Для получения
. Для получения 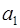 , сперва
, сперва 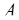 –
– 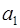 представим в остаточном коде. Очевидно
представим в остаточном коде. Очевидно 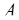 –
– 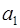 делится на
делится на 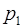 . Более того,
. Более того, 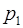 взаимно просто со всеми другими модулями. Следовательно, для нахождения цифры
взаимно просто со всеми другими модулями. Следовательно, для нахождения цифры 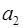 может быть использована процедура деления без остатка:
может быть использована процедура деления без остатка: 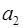 =
= 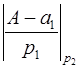 . Таким путем, с помощью вычитаний и делений в остаточной записи все цифры ОПС могут быть получены. При этом замечено, что
. Таким путем, с помощью вычитаний и делений в остаточной записи все цифры ОПС могут быть получены. При этом замечено, что 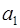 =
=  ,
, 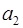 =
= 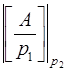 ,
,
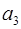 =
= 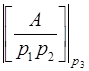 и, вообще, для
и, вообще, для 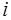 > 1
> 1 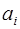 =
= 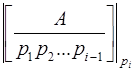 .
.
Перевод, осуществляемый согласно алгоритму (3.6´),содержит всего 2( 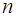 –1) остаточные арифметические операции вычитания и деления без остатка, где
–1) остаточные арифметические операции вычитания и деления без остатка, где 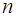 – число модулей системы. Можно предложить некоторую модификацию, т. е. операция деления заменить операцией умножения. Для этого предварительно вычисляется
– число модулей системы. Можно предложить некоторую модификацию, т. е. операция деления заменить операцией умножения. Для этого предварительно вычисляется 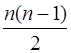 констант
констант 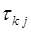 , которые удовлетворяют условию
, которые удовлетворяют условию
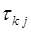
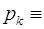 1(
1( 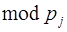 ), 1 ≤
), 1 ≤  <
<  ≤
≤ 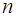 . (3.7´)
. (3.7´)
Эти константы можно, например получить из расширенного алгоритма Евклида
|
|
|
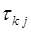
 = 1 (3.8´)
= 1 (3.8´)
Здесь следует заметить тот факт, что константы 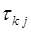 полностью определяются выбранной системой оснований, поэтому могут быть вычислены заранее и храниться в некоторой таблице. В приложении к [90] для модулей
полностью определяются выбранной системой оснований, поэтому могут быть вычислены заранее и храниться в некоторой таблице. В приложении к [90] для модулей 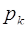 и
и 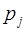 не превосходящих 31 представлена таблица величин
не превосходящих 31 представлена таблица величин 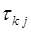 .
.
Если константы 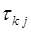 вычислены, то вычисление цифр
вычислены, то вычисление цифр 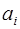 ОПС по алгоритму (3.6´) может быть переписано в виде:
ОПС по алгоритму (3.6´) может быть переписано в виде:
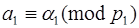 ,
,
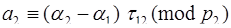 , (3.9´)
, (3.9´)
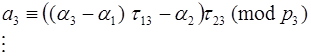 ,
,
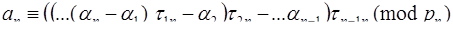 .
.
Константы 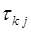 принято также записывать в виде
принято также записывать в виде 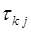 =
=  и называть обратными элементами по умножению для чисел
и называть обратными элементами по умножению для чисел 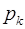 по модулю
по модулю 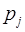 (multiplicative inverse).
(multiplicative inverse).
Рассмотрим алгоритм (3.9´) на примере.
Пример. Пусть дана система оснований 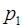 = 2,
= 2,  = 3,
= 3,  = 5,
= 5, 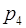 = 7,
= 7, 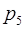 = 11. Объем диапазона
= 11. Объем диапазона 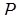 = 2310. переведем число
= 2310. переведем число 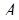 =(1, 1, 3, 5, 4) в ОПС.
=(1, 1, 3, 5, 4) в ОПС.
Найдем сначала константы 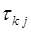 :
:
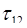 =
=  =2,
=2, 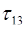 =
= 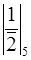 =3,
=3,  =
= 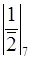 =4,
=4, 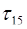 =
=  =6,
=6,
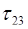 =
= 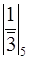 =2,
=2, 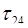 =
=  =5,
=5, 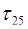 =
= 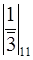 =4,
=4,
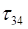 =
= 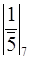 =3,
=3,  =
= 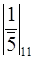 =9,
=9,
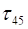 =
=  =8.
=8.
Для удобства константы 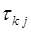 запишем в виде матрицы
запишем в виде матрицы 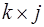 :
:

Выполнение алгоритма (3.9´) представлено в таблице
Перевод числа из СОК в ОПС
|
Действия | Модули |
Цифры ОПС | ||||
 = 2 = 2
| 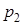 = 3 = 3
| 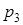 = 5 = 5
|  = 7 = 7
| 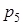 = 11 = 11
| ||
 –
–

| 1
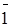
| 2 1 | 1 1 | 4 1 | 7 1 | 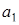 = =  =1 =1
|
 – – 
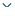

| 0 | 1 2 | 0 3 | 3 4 | 6 6 | |
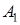 –
–
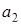
| – | 2 2 | 0 2 | 5 2 | 3 2 | 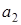 = 2 = = 2 = 
|
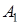 – – 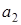
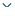
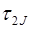
| 0 | 3 2 | 3 5 | 1 4 | ||
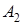 –
–
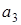
| – | 1
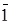
| 1 1 | 4 1 | 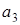 = 1 = = 1 = 
| |
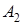 – – 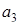
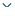

| 0 | 0 3 | 3 9 | |||
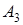 –
–
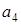
| 0

| 5 0 | 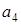 = 0 = = 0 = 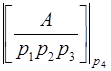
| |||
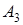 – – 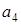
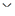
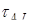
| 0 | 5 8 | ||||
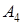
| 7 – | 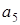 = 7 = = 7 = 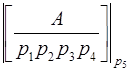
| ||||
Таким образом,
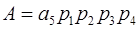 +
+ 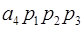 +
+  +
+  +
+ 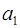 =
=
= 7 · 2 · 3 ·5 · 7 + 0 · 2 · 3 · 5 + 1 · 2 · 3 + 2 · 2 + 1 = 1481.
Преимущество рассмотренного метода перед методом ортогональных базисов состоит в том, что все вычисления выполняются в модулярной арифметике, причем в отдельных каналах, соответствующих модулям 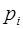 , правда, к сожалению, не параллельно. Рассмотрим некоторые модификации изложенного метода.
, правда, к сожалению, не параллельно. Рассмотрим некоторые модификации изложенного метода.
Один из вариантов уменьшения числа операций в рассмотренном алгоритме может быть достигнут путём особого выбора системы оснований. Выберем систему оснований СОК следующим образом:
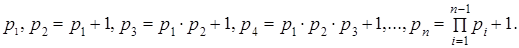
Очевидно, что основания такой системы взаимно простые числа. Эта система обладает той особенностью, что 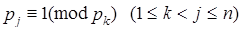 , т.е. из сравнений
, т.е. из сравнений 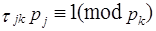 получаем, что все константы
получаем, что все константы 
 = 1. При таком выборе системы оснований алгоритм можно видоизменить следующим образом: вычисления начинают со старших модулей, тогда, т.к. константы
= 1. При таком выборе системы оснований алгоритм можно видоизменить следующим образом: вычисления начинают со старших модулей, тогда, т.к. константы 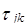 = 1, то в алгоритме отпадает необходимость умножать на
= 1, то в алгоритме отпадает необходимость умножать на 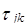 , т.е.
, т.е.
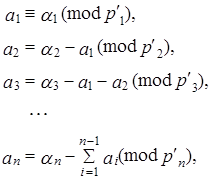 (3.10´)
(3.10´)
где 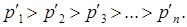
Пример. Выберем систему оснований по указанному принципу:
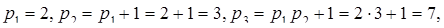
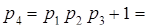
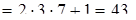 Объём диапазона
Объём диапазона 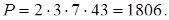
Введем новые обозначения
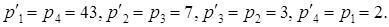
Пусть в системе оснований 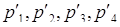 задано число
задано число 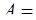 (27, 0, 1, 1). Переведём его в ОПС с той же системой оснований.
(27, 0, 1, 1). Переведём его в ОПС с той же системой оснований.
Метод перевода чисел из СОК в ОПС на основе выбора системы оснований
| Действия | Модули | Цифры ОПС | ||||||||

|
|
|
| |||||||
– 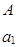
| 27 27 | 0 6 | 1 0 | 1 1 |
| |||||
– 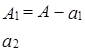
| – |
| 1 1 | 0 1 |
| |||||
– 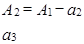
|
| –
|
| 1 0 |
| |||||
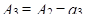
|
|
| – | 1 |
| |||||
Таким образом,
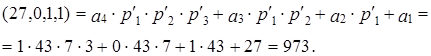
Как видно, при указанном выборе системы оснований число операций уменьшается вдвое, т.к. необходимо для осуществления перевода совершить 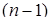 операцию вычитания, против
операцию вычитания, против 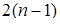 операций в общем случае. Кроме того отпадает необходимость вычислять и хранить константы
операций в общем случае. Кроме того отпадает необходимость вычислять и хранить константы 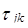 . Похожим свойством обладают системы оснований
. Похожим свойством обладают системы оснований
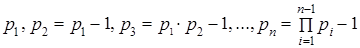 ,
,
для которых все константы  . Однако, главный недостаток указанных систем состоит в быстром росте оснований системы, так как
. Однако, главный недостаток указанных систем состоит в быстром росте оснований системы, так как 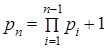 . Один из способов достижения компромисса в создавшемся положении это выбор такой системы оснований, для которой лишь часть констант
. Один из способов достижения компромисса в создавшемся положении это выбор такой системы оснований, для которой лишь часть констант 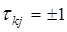 .
.
Другая модификация алгоритма (3.9´) основывается на факте, что если в процессе перевода появляется определенная комбинация цифр, то оставшиеся цифры числа в ОПС можно сразу определить и процесс перевода может быть завершен. К условиям, которые могут завершить процесс перевода до выполнения последнего шага алгоритма (3.9´) можно отнести следующие:
1. Если при определении цифры  оказалось, что все другие остаточные цифры равны
оказалось, что все другие остаточные цифры равны 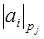 , где
, где  – другие основания СОК (
– другие основания СОК ( 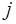 <
< 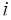 ), тогда остальные цифры ОПС будут нули.
), тогда остальные цифры ОПС будут нули.
2. Если при определении цифры  оказалось, что все другие остаточные цифры равны
оказалось, что все другие остаточные цифры равны 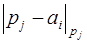 , где
, где  – другие основания СОК (
– другие основания СОК ( 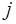 >
> 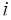 ), тогда
), тогда 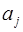 =
=  –1.
–1.
Рассмотрим примеры, иллюстрирующие эти случаи.
Пример. Пусть основания системы 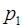 = 2,
= 2, 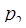 = 3,
= 3, 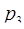 = 5,
= 5, 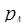 = 7,
= 7, 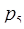 = 11 объем диапазона
= 11 объем диапазона 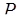 = 2310.
= 2310.
Переведем числа 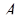 =(1, 2, 3, 2, 1) и
=(1, 2, 3, 2, 1) и 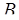 =(1, 0, 2, 4, 8) в ОПС с той же системой оснований. Учтем, что константы
=(1, 0, 2, 4, 8) в ОПС с той же системой оснований. Учтем, что константы 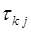 для этой системы вычислены ранее, выпишем их в виде матрицы
для этой системы вычислены ранее, выпишем их в виде матрицы 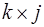 :
:

Для числа 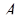 получаем
получаем
Метод перевода числа 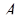 в ОПС по условию получения комбинации цифр
в ОПС по условию получения комбинации цифр
|
Действия | Модули |
Цифры ОПС | ||||
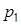 = 2 = 2
| 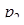 = 3 = 3
|  = 5 = 5
|  = 7 = 7
| 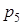 = 11 = 11
| ||
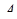 –
–
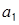
| 1
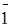
| 2 1 | 3 1 | 2 1 | 1 1 | 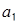 =1 =1
|
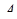 – – 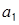

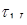
| 0 | 1 2 | 2 3 | 1 4 | 0 6 | |
 –
–

| 2
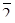
| 1 2 | 4 2 | 0 2 | 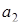 = 2 = 2
| |
 – – 

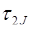
| 0 | 4 2 | 2 5 | 9 4 | ||
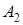
| 3 | 3 | 3 | 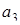 = 3 = 3
| ||
Тогда согласно пункту 1, 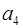 =
= 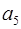 = 0. Таким образом,
= 0. Таким образом,
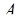 =(1, 2, 3, 2, 1)= = 0 · 2 · 3 ·5 · 7 + 0 · 2 · 3 · 5 + 3 · 2 · 3 + 2 · 2 + 1 = 23.
=(1, 2, 3, 2, 1)= = 0 · 2 · 3 ·5 · 7 + 0 · 2 · 3 · 5 + 3 · 2 · 3 + 2 · 2 + 1 = 23.
Для числа 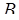 получаем
получаем
Метод перевода числа  в ОПС по условию получения комбинации цифр
в ОПС по условию получения комбинации цифр
|
Действия | Модули |
Цифры ОПС | ||||
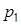 = 2 = 2
| 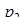 = 3 = 3
| 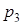 = 5 = 5
| 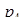 = 7 = 7
| 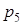 = 11 = 11
| ||
 –
–
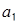
| 1
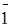
| 0 1 | 2 1 | 4 1 | 8 1 |
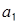 =1 =1
|
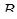 – – 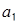

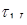
| 0 | 2 2 | 1 3 | 3 4 | 7 6 | |
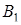 –
–
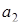
| 1
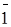
| 3 1 | 5 1 | 9 1 | 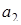 = 1 = 1
| |
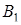 – – 

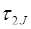
| 0 | 2 2 | 4 5 | 8 4 | ||
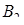
| 4 | 6 | 10 | 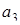 = 4 = 4
| ||
Тогда согласно пункту 2, 
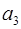 = 4,
= 4,  = 6,
= 6, 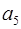 = 10.
= 10.
Таким образом
, 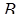 = (1, 0, 2, 4, 8) = 10 · 2 · 3 ·5 · 7 + 6 · 2 · 3 · 5 + 4 · 2 · 3 + 1 · 2 + 1 = 2307.
= (1, 0, 2, 4, 8) = 10 · 2 · 3 ·5 · 7 + 6 · 2 · 3 · 5 + 4 · 2 · 3 + 1 · 2 + 1 = 2307.
При использовании предложенного метода число операций в процессе перевода чисел в ОПС уменьшается. Причем наибольшая выгода наблюдается при небольших по абсолютной величине основаниях системы. Было подсчитано, что при использовании рассмотренных приемов число операций в процессе перевода числа из СОК в ОПС, например, для системы модулей 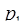 = 13,
= 13, 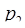 = 11,
= 11, 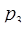 = 7,
= 7, 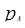 = 5,
= 5,  = 3,
= 3, 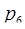 = 2, будет в среднем 6,4, против 10 остаточных операций при применении стандартного метода. Однако, для проверки условий, позволяющих завершить процесс перевода. Потребуется наличие дополнительных логических устройств.
= 2, будет в среднем 6,4, против 10 остаточных операций при применении стандартного метода. Однако, для проверки условий, позволяющих завершить процесс перевода. Потребуется наличие дополнительных логических устройств.
Еще можно отметить, что специальный выбор оснований СОК может позволить вычисление констант 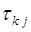 . Так, при кодировании остатков в двоичной системе бывает удобно выбирать модули СОК в виде
. Так, при кодировании остатков в двоичной системе бывает удобно выбирать модули СОК в виде
 =
= 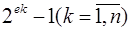 . (3.11´)
. (3.11´)
Тогда для определения констант 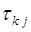 существует достаточно простая формула
существует достаточно простая формула
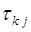 = 1+
= 1+ 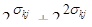 +…+
+…+ 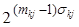 , (3.12´)
, (3.12´)
где целые числа 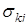 и
и 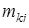 подбираются из условий
подбираются из условий
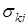
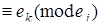 ,
, 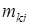
 . (3.13´)
. (3.13´)
3). Достаточно эффективными методами перевода чисел из СОК в ПСС являются интервальные методы, основанные на интервальных характеристиках чисел. Одна из таких характеристик – номер интервала.
Рассмотрим СОК, заданную системой оснований 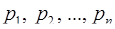 , с объёмом диапазона
, с объёмом диапазона  . Выберем дробящий модуль
. Выберем дробящий модуль  и проведём дробление заданного диапазона на интервалы путём деления
и проведём дробление заданного диапазона на интервалы путём деления  на модуль
на модуль 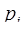 . Тогда количество интервалов
. Тогда количество интервалов 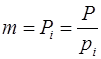 , а длина интервала определяется величиной модуля. В результате величину любого числа
, а длина интервала определяется величиной модуля. В результате величину любого числа 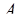 , заданного в СОК по выбранным основаниям можно определить по номеру интервала:
, заданного в СОК по выбранным основаниям можно определить по номеру интервала:
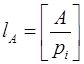 , (3.14´)
, (3.14´)
в котором находится число 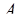 и по цифре
и по цифре 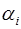 числа
числа 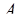
 в СОК по модулю
в СОК по модулю 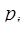 , т.е.
, т.е.
 . (3.15´)
. (3.15´)
Так как ( 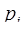 ,
, 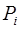 ) = 1, то по теореме Эйлера:
) = 1, то по теореме Эйлера:
 , (3.16´)
, (3.16´)
где 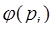 – функция Эйлера. Причём если
– функция Эйлера. Причём если 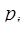 – простое число, то
– простое число, то  =
= 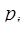 –1. Подставляя (3.15´) в (3.4´), учитывая (3.1´) и (3.4´) число
–1. Подставляя (3.15´) в (3.4´), учитывая (3.1´) и (3.4´) число 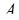 можно записать в виде
можно записать в виде
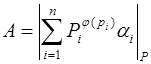 . (3.17´)
. (3.17´)
Для определения номера интервала  подставим (3.17´) в (3.14´):
подставим (3.17´) в (3.14´):
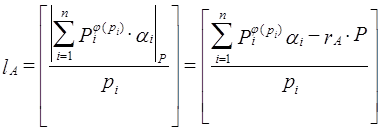 . (3.18´)
. (3.18´)
Учитывая, что 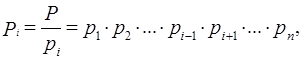 перепишем (3.18´) в виде
перепишем (3.18´) в виде
 . (3.19´)
. (3.19´)
Так как 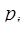 является делителем чисел
является делителем чисел 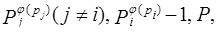 то
то

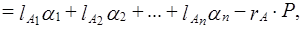
где
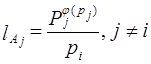 и
и 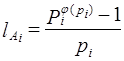 –
–
постоянные коэффициенты, определённые системой оснований.
Таким образом,
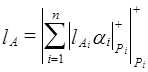 . (3.20´)
. (3.20´)
Подставляя (3.20´) в (3.15´), получим позиционное представление числа 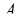
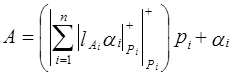 . (3.21´)
. (3.21´)
В качестве дробирующего модуля целесообразнее выбирать наибольший из модулей системы. В этом случае модульные операции выполняются при меньшей величине модуля, что ведёт к меньшим временным и аппаратурным затратам. Целесообразно также для упрощения вычислений и минимизации времени выполнения операций выбирать в качестве дробирующего модуля  наибольшие модули системы, представляющие числа Мерсенна
наибольшие модули системы, представляющие числа Мерсенна 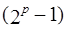 или Ферма
или Ферма 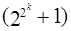 . При этом предпочтение отдаётся числам Мерсенна, так как арифметика по этим модулям проще.
. При этом предпочтение отдаётся числам Мерсенна, так как арифметика по этим модулям проще.
Проиллюстрируем рассмотренный метод на примере.
Пример. Пусть дана система оснований  тогда
тогда 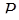 = 210. Пусть надо перевести число
= 210. Пусть надо перевести число 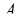 =(0,1,4,3). В качестве дробирующего модуля выберем
=(0,1,4,3). В качестве дробирующего модуля выберем 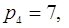 тогда
тогда  , номер интервала
, номер интервала  , а само число
, а само число  . Определим
. Определим 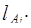 Так как
Так как
 то
то
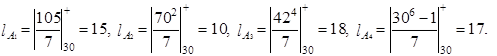
Тогда 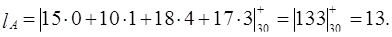
Таким образом,  13·7 + 3 = 94.
13·7 + 3 = 94.
На основе этой же характеристики числа – номера интервала, с применением теоремы Эйлера предлагается алгоритм перевода числа в ПСС. Разность между модулями можно представить в виде 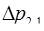 =
= 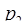 –
–  и тогда
и тогда
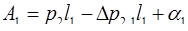 , (3.22´)
, (3.22´)
но с другой стороны
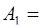
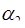 (
( 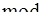
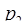 ). (3.23´)
). (3.23´)
Из (3.22´) и (3.23´) следует, что 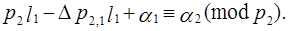
Так как 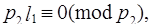
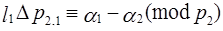 . (3.24´)
. (3.24´)
Решение сравнения (3.24´) можно записать в виде
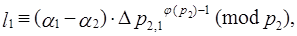 (3.25´)
(3.25´)
где 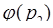 – функция Эйлера. Если
– функция Эйлера. Если 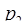 – простое число, то
– простое число, то  Поэтому в случае простого
Поэтому в случае простого 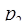 выражение (2.3.13) примет вид:
выражение (2.3.13) примет вид:
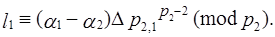
Перепишем (3.15´) с учётом (3.25´)
 (3.26´)
(3.26´)
где 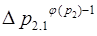 – константа, определяемая выбором оснований СОК. Нетрудно заметить, что
– константа, определяемая выбором оснований СОК. Нетрудно заметить, что 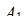 – наименьший неотрицательный вычет по составному модулю
– наименьший неотрицательный вычет по составному модулю 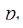 ·
· 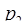 . Исходя из этого можно записать:
. Исходя из этого можно записать:
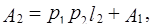 (3.27´)
(3.27´)
где 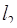 показывает, сколько раз произведение
показывает, сколько раз произведение 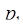 ·
· 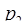 укладывается в числе
укладывается в числе 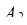 . Для нахождения
. Для нахождения 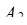 можно считать, что число
можно считать, что число 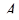 представлено в системе оснований
представлено в системе оснований 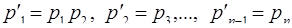 в виде
в виде 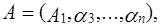 и после этого можно воспользоваться формулой (3.27´). Проводя аналогичные рассуждения, после преобразований получим:
и после этого можно воспользоваться формулой (3.27´). Проводя аналогичные рассуждения, после преобразований получим:
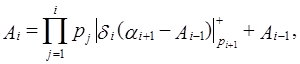 (3.28´)
(3.28´)
Где
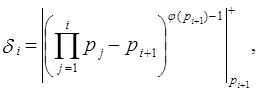
 (3.29´)
(3.29´)
Тогда искомая величина числа 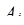 (
( 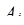 – наименьший неотрицательный вычет числа
– наименьший неотрицательный вычет числа 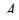 по составному модулю
по составному модулю 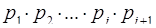 ) определяется за
) определяется за 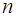 – 1 шагов, где
– 1 шагов, где 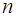 – число оснований СОК.
– число оснований СОК.
Пример. Пусть основания СОК 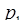 = 3,
= 3,  = 5,
= 5, 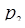 = 7,
= 7, 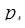 = 11, объём диапазона
= 11, объём диапазона 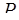 = 1155. Найдём величину числа
= 1155. Найдём величину числа 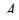 = (1,2,0,8).
= (1,2,0,8).
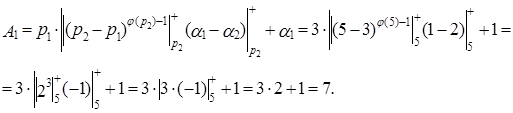
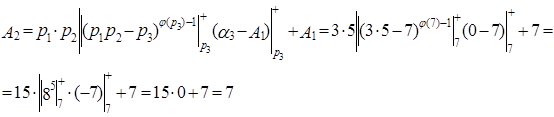
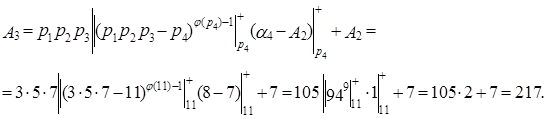
§ 4. Расширение диапазона представления чисел
Расширение системы оснований является одной из основных немодульных операций в СОК. Выполнение этой операции бывает необходимо при выполнении операции деления чисел, при вычислении позиционных характеристик, при обнаружении переполнения при выполнении сложения или умножения чисел.
Задачу расширения системы оснований можно сформулировать следующим образом: найти остаточное представление числа по новому основанию (новым основаниям), если известно представление числа по другим основаниям остатки от деления на другие числа.
Один из путей расширения системы оснований состоит в переводе числа в позиционную систему счисления и вычисления остатка от деления на новый модуль. Этот путь не является рациональным с точки зрения числа операций.
Другой метод расширения системы оснований позволяет определить цифру числа по новому основанию, базируясь на таких позиционных характеристиках числа, как ранг числа, след числа. Пусть вновь задана система оснований 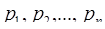 с диапазоном Р, ортогональными базисами
с диапазоном Р, ортогональными базисами 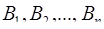 , веса которых
, веса которых 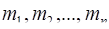 . По определению,
. По определению, 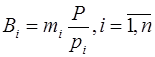 . Пусть в этой системе задано число
. Пусть в этой системе задано число 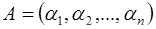 . Расширим систему оснований, добавляя основание
. Расширим систему оснований, добавляя основание  , тогда диапазон системы станет
, тогда диапазон системы станет 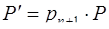 , ортогональные базисы системы
, ортогональные базисы системы 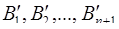 , их веса
, их веса 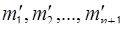 , причём
, причём 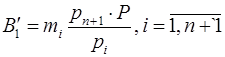 . Задача состоит в определении цифры
. Задача состоит в определении цифры 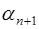 числа
числа 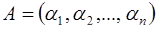 по основанию
по основанию  называют цифру
называют цифру 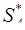 , при которой число
, при которой число 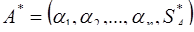 находится в интервале
находится в интервале 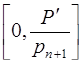 , и что число
, и что число 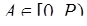 , то определение цифры по основанию
, то определение цифры по основанию  сводится к определению минимального следа числа А в расширенной системе оснований.
сводится к определению минимального следа числа А в расширенной системе оснований.
Чтобы получить формулы для цифры 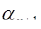 запишем выражение для числа А в основной и расширенной системах:
запишем выражение для числа А в основной и расширенной системах:
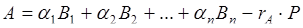 и
и 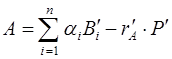 ,
,
где 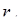 и
и  - ранги числа А в основной и расширенной системах.
- ранги числа А в основной и расширенной системах.
Приравнивая правые части этих выражений, определяем 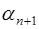 :
:
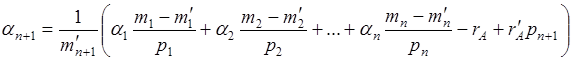
, или обозначая через 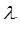 целое число
целое число 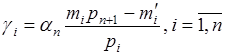 , а через
, а через  величину
величину  , получаем
, получаем 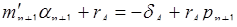 . Наконец, представляя
. Наконец, представляя  в виде
в виде 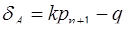 , где k , q – целые неотрицательные числа и
, где k , q – целые неотрицательные числа и 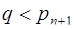 , получаем
, получаем
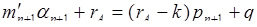 , или
, или
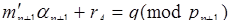 . (4.1´)
. (4.1´)
Формула (4.1´) и есть формула расширения диапазона чисел.
Для практической реализации этой формулы поступают следующим образом:
1. Вычисляют параметры основной и расширенной систем (ортогональные базисы, их веса, минимальные псевдоортогональные числа с их рангами и кратности).
2. Конструируют число 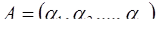 из минимальных псевдоортогональных чисел
из минимальных псевдоортогональных чисел 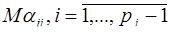 ,
, 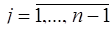 , с рангами
, с рангами  , которые однозначно определяются выбранной системой оснований
, которые однозначно определяются выбранной системой оснований 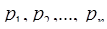 . В результате, получают число
. В результате, получают число 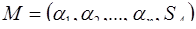 , где
, где  - след числа, а его ранг находят по теореме о ранге суммы:
- след числа, а его ранг находят по теореме о ранге суммы:
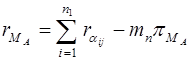 , (4.2´)
, (4.2´)
где 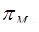 - число переходов по основанию
- число переходов по основанию 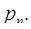
3. Расширяют число 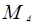 по формуле расширения (4.1´). Пользуясь величиной ранга
по формуле расширения (4.1´). Пользуясь величиной ранга 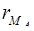 , вычисленной по формуле (4.2´), получают число
, вычисленной по формуле (4.2´), получают число 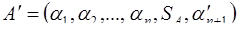 , которое отличается от искомого числа А цифрами по двум последним основаниям.
, которое отличается от искомого числа А цифрами по двум последним основаниям.
4. Если 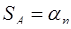 , то
, то 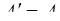 , т. е.
, т. е. 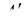 - искомое расширение числа А.
- искомое расширение числа А.
5. Если 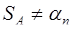 , то прибавляют к числу
, то прибавляют к числу 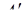 такое из минимальных псевдоортогональных чисел
такое из минимальных псевдоортогональных чисел 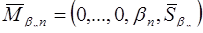 кратности
кратности 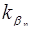 , где
, где 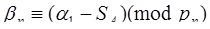 , которое превратит цифру по основанию
, которое превратит цифру по основанию 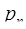 в
в 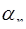 . В результате, получают число
. В результате, получают число 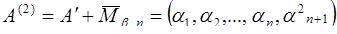 .
.
6. Если кратность 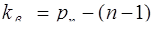 , то число
, то число 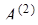 является искомым расширением числа А, так как к числу
является искомым расширением числа А, так как к числу 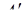 , не превышающему
, не превышающему 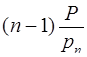 прибавили число
прибавили число 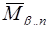 , не превышающее
, не превышающее 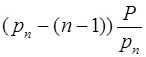 , т. е.
, т. е.  не превышает Р, т. е. величины 1-го интервала.
не превышает Р, т. е. величины 1-го интервала.
7. Если  , то число
, то число 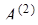 может располагаться либо в последних
может располагаться либо в последних 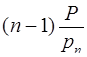 частях 1-го интервала [0; P), либо в младших
частях 1-го интервала [0; P), либо в младших 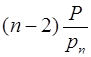 частях второго интервала [P; 2P), а тогда искомым является число
частях второго интервала [P; 2P), а тогда искомым является число 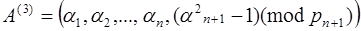 .
.
Еще один путь решения поставленной задачи представляет собой перевод числа из СОК в ОПС с дополнительным финальным шагом. Рассмотрим этот метод.
Пусть СОК состоит из оснований 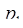 ,
,  , …,
, …, 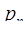 . Объем диапазона этой системы будет
. Объем диапазона этой системы будет  . Добавим к числу оснований СОК новое основание
. Добавим к числу оснований СОК новое основание  . Объем диапазона этой системы
. Объем диапазона этой системы 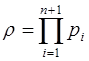 . Тогда любое число
. Тогда любое число 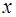 из диапазона [0;
из диапазона [0;  ) в обобщенной позиционной системе счисления представимо в виде
) в обобщенной позиционной системе счисления представимо в виде 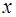 =
= 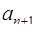
 +
+ 
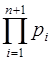 +…+
+…+ 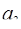
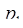
 +
+ 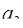
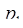 +
+ 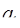 . Если число
. Если число 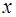 будет лежать в первоначальном диапазоне [0;
будет лежать в первоначальном диапазоне [0; 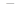 ), то в ОПС цифра
), то в ОПС цифра 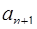 = 0. Этот факт и используется для получения остатка от деления числа
= 0. Этот факт и используется для получения остатка от деления числа 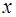 на новое основание СОК
на новое основание СОК 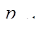 .
.
Пусть число 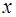 имело представление (
имело представление ( 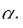 ,
, 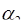 , …,
, …,  ) по основаниям
) по основаниям 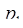 ,
,  , …,
, …, 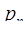 . Добавляем новое основание
. Добавляем новое основание 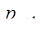 , тогда число
, тогда число 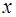 =(
=( 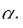 ,
,  , …,
, …,  ,
, 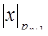 ) в системе оснований
) в системе оснований 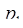 ,
,  , …,
, …, 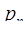 ,
, 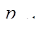 , где
, где 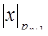 – остаток от деления числа
– остаток от деления числа 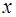 на
на 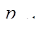 , т.е. искомая цифра по новому основанию.
, т.е. искомая цифра по новому основанию.
Для определения этой цифры рассматриваем алгоритм перевода числа из СОК в ОПС, включая неизвестную цифру 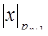 в проводимые операции. При этом мы последовательно будем получать цифры ОПС
в проводимые операции. При этом мы последовательно будем получать цифры ОПС 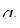 ,
, 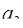 , …,
, …,  и выражение для цифры
и выражение для цифры 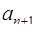 . Но так как по предположению число
. Но так как по предположению число 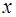
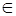 [ 0;
[ 0;  ), то цифра
), то цифра 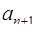 = 0. Из полученного соотношения и определяем искомую цифру
= 0. Из полученного соотношения и определяем искомую цифру 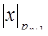 .
.
Пример. Пусть задана система модулей 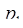 = 2,
= 2, 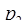 = 3,
= 3,  = 5,
= 5, 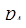 = 7, тогда
= 7, тогда  = 2·3·5·7=210. И пусть задано число
= 2·3·5·7=210. И пусть задано число 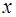 = 157= (1, 1, 2, 3). Расширим систему оснований, добавляя
= 157= (1, 1, 2, 3). Расширим систему оснований, добавляя 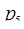 = 11. Пусть
= 11. Пусть 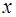 = (1, 1, 2, 3,
= (1, 1, 2, 3, 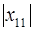 ) в системе оснований
) в системе оснований 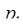 = 2,
= 2, 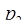 = 3,
= 3,  = 5,
= 5, 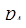 = 7,
= 7, 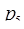 = 11. Набор констант
= 11. Набор констант  =
=  задается матрицей
задается матрицей
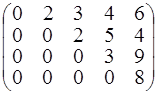
Процесс решения задачи покажем
Расширение оснований модулярного кода
| Действия | Модули | Цифры СОК | ||||
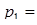 2 2
|  3 3
| 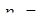 5 5
|  7 7
|  11 11
| ||
| _ х а1 | 1 1 | 1 1 | 2 1 | 3 1 | 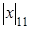 1
1
| а1=0 |
х-а1
´
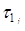
| 0 | 0 2 | 1 3 | 2 4 | 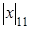 -1
6 -1
6
| |
| _ х1 а2 | 0 0 | 3 0 | 1 0 | 6 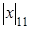 -6
0 -6
0
| а2=0 | |
х1-а2
´

| 0 | 3 2 | 1 5 | 6 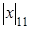 -6
4 -6
4
| ||
| _ х2 а3 | 1 1 | 5 1 | 2 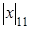 -2
1 -2
1
| а3=1 | ||
х2-а3
´
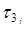
| 0 | 4 3 | 2 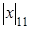 -3
9 -3
9
| |||
| _ х3 а4 | 5 5 | 7 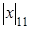 -5
5 -5
5
| А4=5 | |||
х3-а4
´

| 0 | 7 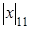 -10
8 -10
8
| ||||
| x4 | 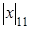 -3 -3
| а5= 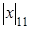 -3 -3
| ||||
Таким образом, а5 = 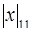 – 3, но по условию а5 = 0, т.е.
– 3, но по условию а5 = 0, т.е. 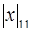 – 3 = 0, откуда
– 3 = 0, откуда 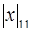 = 3. Получим расширенное представление числа
= 3. Получим расширенное представление числа 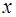 = 157 = (1, 1, 2, 3, 3) по основаниям
= 157 = (1, 1, 2, 3, 3) по основаниям
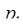 = 2,
= 2, 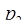 = 3,
= 3, 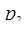 = 5,
= 5, 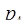 = 7,
= 7, 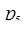 = 11.
= 11.
Этот алгоритм может быть несколько видоизменен за счет следующего свойства:

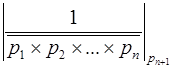 .
.
Фактически величина 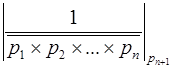 используется только на последнем шаге определения цифры
используется только на последнем шаге определения цифры  . Поэтому в столбце по новому основанию
. Поэтому в столбце по новому основанию 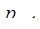 с самого начала можно записать ноль и применить алгоритм перевода числа из СОК в ОПС.
с самого начала можно записать ноль и применить алгоритм перевода числа из СОК в ОПС.
Пусть по этому алгоритму будет получено что  =
=  для числа (
для числа ( 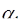 ,
, 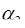 , …,
, …,  , 0). Тогда
, 0). Тогда  для числа
для числа 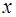 можно найти из соотношения:
можно найти из соотношения:
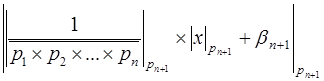 = 0.
= 0.
Рассмотрим на том же примере эту модификацию алгоритма.
Модифицированный метод расширения оснований модулярного кода
| Действия | Модули | Цифры СОК | ||||
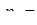 2 2
| 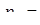 3 3
| 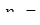 5 5
| 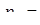 7 7
| 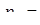 11 11
| ||
| _ х а1 | 1 1 | 1 1 | 2 1 | 3 1 | 0 1 | А1=1 |
х-а1
´

| 0 | 0 2 | 1 3 | 2 4 | 10 6 | |
| _ х1 а2 | 0 0 | 3 0 | 1 0 | 5 0 | А2=0 | |
х1-а2
´

| 0 | 3 2 | 1 5 | 5 4 | ||
| _ х2 а3 | 1 1 | 5 1 | 9 1 | А3=1 | ||
х2-а3
´
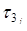
| 0 | 4 3 | 8 9 | |||
| _ х3 а4 | 5 5 | 6 5 | А4=5 | |||
х3-а4
´

| 0 | 1 8 | 
| |||
| x4 | 8 | 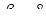
| ||||
Тогда 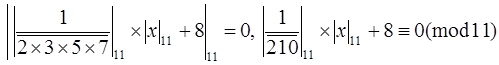 ,
,
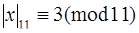 . Заметим также, что последние умножение на
. Заметим также, что последние умножение на 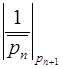 можно не проводить.
можно не проводить.
Тогда финальный шаг для определения цифры по новому основанию может быть записан как 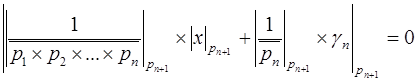 , или умножая на
, или умножая на  , получим
, получим 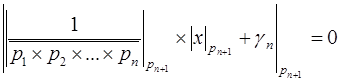 , где
, где 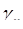 - цифра, полученная по основанию
- цифра, полученная по основанию 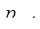 после вычитания цифры
после вычитания цифры  . В нашем примере
. В нашем примере 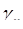 = 1. Таким образом, искомую цифру можно определить из соотношения:
= 1. Таким образом, искомую цифру можно определить из соотношения: 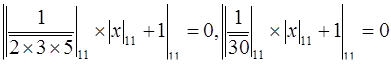 , откуда
, откуда
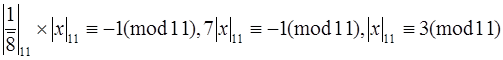 .
.
Так как результат образования цифры в СОК по новому основанию 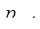 зависит только от первых цифр, то операцию расширения можно проводить сразу по нескольким основаниям.
зависит только от первых цифр, то операцию расширения можно проводить сразу по нескольким основаниям.
Пример. Пусть задана система оснований
 ,
,
объем диапазона 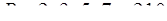 . И пусть задано число
. И пусть задано число 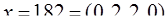 в этой системе оснований.
в этой системе оснований.
Найдем расширенное представление этого числа, добавляя модули 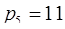 и
и 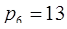 .
.
Для этого запишем нули в качестве неизвестных цифр и примем вышерассмотренный алгоритм расширения системы оснований.
Константы 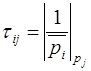 вычислены заранее и записаны в виде матрицы
вычислены заранее и записаны в виде матрицы
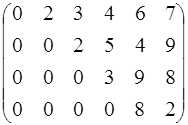
Тогда получаем
Расширение модулярного кода по нескольким основаниям
| Действия | Модули | Цифры СОК | |||||
| 
| 
| 
| 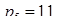
| 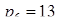
| ||
| _ х а1 | 0 0 | 2 0 | 2 0 | 0 0 | 0 0 | 0 0 | а1=0 |
х-а1
´
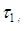
| 0 | 2 2 | 2 3 | 0 4 | 0 6 | 0 7 | |
| _ х1 а2 | 1 1 | 1 1 | 0 1 | 0 1 | 0 1 | а2=1 | |
х1-а2
´

| 0 | 0 2 | 6 5 | 10 4 | 12 9 | ||
| _ х2 а3 | 0 0 | 2 0 | 7 0 | 4 0 | а3=0 | ||
х2-а3
´
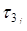
| 0 | 2 3 | 7 9 | 4 8 | |||
| _ х3 а4 | 6 6 | 8 6 | 6 6 | а4=6 | |||
х3-а4
´

| 0 | 2 8 | 0 2 | ||||
| x4 | 5 | 0 | |||||
Цифры по основаниям  и
и 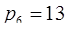 находим из соотношений:
находим из соотношений:
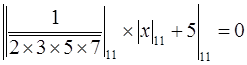 и
и 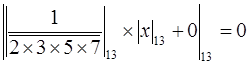 ,
,
откуда получаем 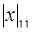 = 6 и
= 6 и 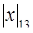 = 0.
= 0.
Таким образом, число 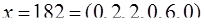 в этой системе оснований
в этой системе оснований
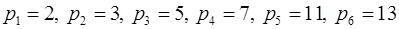 .
.
Преимущества метода расширения системы основания с помощью перевода в ОПС состоит в том, что:
во-первых, все вычисления идут в параллельных каналах по определенным модулям;
во-вторых, не требуется вычисление большого количества дополнительных величин (необходимо наличие в памяти только констант 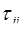 );
);
в-третьих, возможно получение расширенного представления числа сразу по нескольким дополнительным основаниям, что не влияет на быстродействие всей операции.
Дата добавления: 2019-07-15; просмотров: 243; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!