Теорема о делении с остатком. Алгоритм Евклида
Введение
Инженеры и программисты, а также математики знакомы с таким понятием как цифровая обработка сигналов. Напомним некоторые факты.
Сигнал называется цифровым, если область значений последовательности ограничена конечным множеством действительных или комплексных чисел.
Обработка сигналов универсальными цифровыми вычислительными машинами или специализированными цифровыми процессорами осуществляется путём выполнения ряда вычислительных операций над последовательностями чисел. В настоящее время существует несколько алгоритмов, предназначенных для использования в области цифровой обработки сигналов. Здесь же немалую роль играет система остаточных классов, основанная на элементарной теории чисел.
Вообще, идею теории чисел для получения алгоритмов вычислений используют в 2-х наиболее важных направлениях обработки сигналов:
- в вычислении свёртки;
- в вычислении дискретного преобразования Фурье.
Цель же дипломной работы:
- установить взаимосвязь СОК и теории чисел;
- изучить СОК и методы перевода чисел из ПСС в СОК и обратно;
- разработать и выполнить программы на языке Paskal, содержащие различные методы перевода чисел из ПСС в СОК и обратно.
Дипломная работа состоит из введения, трёх глав и списка литературы.
Во введении даётся краткое обоснование поставленных задач.
Первая глава содержит известные факты теории чисел в той мере, в какой они будут применяться в дальнейшем. Здесь излагаются самые элементарные понятия теории чисел, в частности, сравнения и их свойства, различные теоремы. А также главная теорема в СОК – китайская теорема об остатках.
|
|
|
Вторая глава посвящена представлению чисел в СОК и различным методам перевода чисел из СОК в ПСС и от ПСС в СОК.
Третья глава содержит программные разработки методов перевода чисел из ПСС в СОК и обратно.
Глава 1. Теоретико-числовая база построения СОК
Сравнения и их основные свойства
Возьмём произвольное фиксированное натуральное число p и будем рассматривать остатки при делении на р различных целых чисел.
При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.
Определение. Целые числа а и b называются сравнимыми по модулю р, если разность чисел а – b делится на р, то есть, если 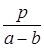 . Соотношение между а, b и р запишем в виде:
. Соотношение между а, b и р запишем в виде:
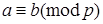 (1.1)
(1.1)
запись mod p будет означать, что 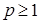 , числа а и b – вычеты.
, числа а и b – вычеты.
Если разность а – b не делится на р, то запишем:
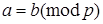 .
.
Согласно определению 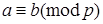 означает, что а делится на р.
означает, что а делится на р.
Примеры:
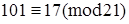 , т. к. 101 – 17 = 84, а
, т. к. 101 – 17 = 84, а  или
или 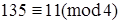 , т. к. числа 135 и 11 при делении на 4 дают остаток 3.
, т. к. числа 135 и 11 при делении на 4 дают остаток 3.
|
|
|
Теорема. а сравнимо с b тогда и только тогда, когда а и b имеют одинаковые остатки при делении на р, поэтому в качестве определения сравнения можно взять следующее:
Определение: Целые числа а и b называются сравнимыми по модулю р, если остатки от деления этих чисел на р равны.
Дадим основные свойства сравнений:
1. Рефлексивность отношения сравнимости:
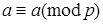
2. Симметричность отношения сравнимости:
если, 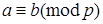 , то
, то  .
.
3. Транзитивность отношения сравнимости:
если  ,
, 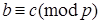 , то
, то 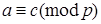 .
.
4. Если  и k – произвольное целое число, то
и k – произвольное целое число, то 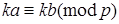 .
.
5. Если 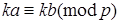 и (k, p) = 1, то
и (k, p) = 1, то 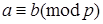 .
.
6. Если  и k – произвольное натуральное число, то
и k – произвольное натуральное число, то  .
.
7. Если 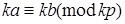 , где k и р – произвольные натуральные числа, то
, где k и р – произвольные натуральные числа, то  .
.
8. Если 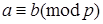 ,
, 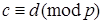 , то
, то 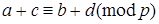 и
и 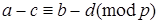 .
.
9. Если 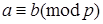 ,
, 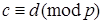 , то
, то 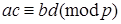 .
.
10. Если  , то при любом целом n > 0,
, то при любом целом n > 0, 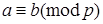 .
.
11. Если  и
и 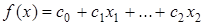 - произвольный многочлен с целыми коэффициентами, то
- произвольный многочлен с целыми коэффициентами, то 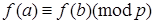 .
.
12. Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть.
13. Если 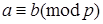 и
и 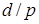 , то
, то  .
.
14. Если  , то множество общих делителей а и р совпадает с множеством общих делителей b и р. В частности,
, то множество общих делителей а и р совпадает с множеством общих делителей b и р. В частности, 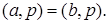
15. Если 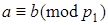 ,
, 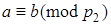 , …,
, …, 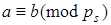 , то
, то 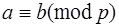 , где
, где 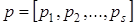 .
.
При делении целого числа на модуль р в остатке получается 0, 1, 2, 3,…, р – 1 чисел.
Отнесём все целые числа, дающие при делении на р один и тот же остаток в один класс, поэтому получится р – различных классов по модулю р.
|
|
|
В один класс попадут равноостаточные числа, они называются вычетами друг друга.
Обозначим через А0 – класс вычетов, которые при делении на р дают остаток 0.
Например, числа вида 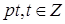 .
.
Через А1 – числа, дающие при делении остаток 1.
Например, числа вида  .
.
Через А2 – числа, дающие при делении остаток 2.
Например, числа вида 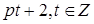 .
.
Через Ар-1 – числа, дающие при делении остаток р – 1.
Например, числа вида 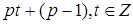 .
.
Полной системой вычетов по модулю р называется совокупность р-целых чисел, содержащая точно по одному представителю из каждого класса вычетов по модулю р. Каждый класс вычетов по модулю р содержит в точности одно из чисел совокупности всех возможных остатков от деления на р: 0, 1, …, р – 1. Множество {0, 1, …, р – 1} называется полной системой наименьших неотрицательных вычетов по модулю р. Можно легко доказать, что любая совокупность р чисел (р >1), попарно несравнимых по модулю р, есть полная система вычетов по модулю р. Часто рассматривают полную систему наименьших положительных вычетов: 1, 2, …, р; полную систему наименьших по абсолютной величине вычетов:
 при чётном р и
при чётном р и
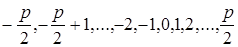 при р нечётном.
при р нечётном.
|
|
|
Можно ввести в рассмотрение приведённую систему вычетов по модулю р, т. е. систему чисел, взятых по одному и только по одному из каждого класса, взаимно простого с модулем.
Число классов, взаимно простых с модулем р, равно значению функции Эйлера φ(р).
Теорема о делении с остатком. Алгоритм Евклида
Рассмотрим пример. Пусть р = 6.
Тогда имеем шесть классов разбиения множества целых чисел по модулю 6:
 r = 0;
r = 0;
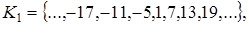 r = 1;
r = 1;
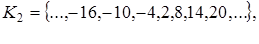 r = 2;
r = 2;
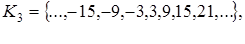 r = 3;
r = 3;
 r = 4;
r = 4;
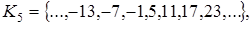 r = 5;
r = 5;
где через r обозначен остаток от деления целого числа на 6.
Напомним теорему о делении с остатком:
Теорема: Разделить число 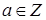 на число
на число 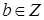 ,
, 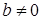 , с остатком, значит, найти пару целых чисел q и r, таких, что выполняются следующие условия:
, с остатком, значит, найти пару целых чисел q и r, таких, что выполняются следующие условия: 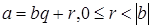 .
.
Легко доказывается, что для любых целых чисел а и 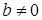 деление с остатком возможно и числа q и r определяются однозначно. В нашем примере полная система наименьших неотрицательных вычетов есть множество {0, 1, 2, 3, 4, 5}; полная система наименьших положительных вычетов – множество {0, 1, 2, 3, 4, 5, 6}; полная система наименьших по абсолютной величине вычетов – множество {-2,-1, 0, 1, 2, 3}; приведённая система вычетов – множество {1,5}, так как
деление с остатком возможно и числа q и r определяются однозначно. В нашем примере полная система наименьших неотрицательных вычетов есть множество {0, 1, 2, 3, 4, 5}; полная система наименьших положительных вычетов – множество {0, 1, 2, 3, 4, 5, 6}; полная система наименьших по абсолютной величине вычетов – множество {-2,-1, 0, 1, 2, 3}; приведённая система вычетов – множество {1,5}, так как 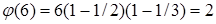 ; фактор-множество
; фактор-множество 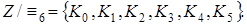
Один из методов выполнения арифметических операций над данными целыми числами основан на простых положениях теории чисел. Идея этого метода состоит в том, что целые числа представляются в одной из непозиционных систем – в системе остаточных классов. А именно: вместо операций над целыми числами оперируют с остатками от деления этих чисел на заранее выбранные простые числа – модули 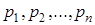 . Чаще всего числа
. Чаще всего числа  выбирают из множества простых чисел.
выбирают из множества простых чисел.
Пусть 
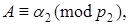 …,
…, 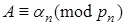 .
.
Так как в кольце целых чисел имеет место теорема о делении с остатком, т. е.  где
где 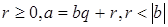 , то кольцо Z, по определению, является евклидовым. Таким образом, в качестве чисел
, то кольцо Z, по определению, является евклидовым. Таким образом, в качестве чисел 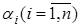 можно выбрать остатки от деления числа А на р i соответственно.
можно выбрать остатки от деления числа А на р i соответственно.
Рассмотрим гомоморфное отображение:
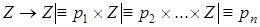 .
.
Тогда каждому целому числу А можно поставить в соответствие кортеж  наименьших неотрицательных вычетов по одному из соответствующих классов.
наименьших неотрицательных вычетов по одному из соответствующих классов.
Важно отметить, что при том нет никакой потери информации при условии, что 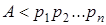 , так как всегда, зная
, так как всегда, зная 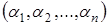 можно восстановить, как мы увидим позже само число А. Поэтому кортеж
можно восстановить, как мы увидим позже само число А. Поэтому кортеж 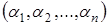 можно рассматривать как один из способов представления целого числа А в компьютере – модулярное представление или представление в системе остаточных классов (СОК).
можно рассматривать как один из способов представления целого числа А в компьютере – модулярное представление или представление в системе остаточных классов (СОК).
Для дальнейшего нам требуется расширенный алгоритм Евклида или его аналог – алгоритм нахождения линейного представления наибольшего общего делителя целых чисел: если числа а и b одновременно не равны нулю, то существуют целые числа х и у, такие, что 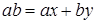 .
.
Действительно, пусть d – наименьшее целое положительное число вида 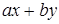 , например,
, например,  , где числа х0 и у0 не обязательно определены однозначно. Существование числа d следует только из принципа полной упорядоченности. Очевидно, что d > 0. Остаётся показать, что
, где числа х0 и у0 не обязательно определены однозначно. Существование числа d следует только из принципа полной упорядоченности. Очевидно, что d > 0. Остаётся показать, что 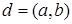 . Для этого надо проверить выполнение двух условий: а)
. Для этого надо проверить выполнение двух условий: а) 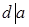 и
и  ; б) если
; б) если 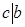 и
и 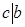 , то
, то 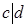 . Допустим, что свойство а) не выполняется и для определённости положим, что |
. Допустим, что свойство а) не выполняется и для определённости положим, что | 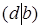 . Тогда по теореме о делении с остатком
. Тогда по теореме о делении с остатком 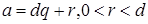 , и, следовательно,
, и, следовательно,
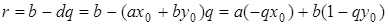 ,
,
что противоречит минимальности d. Выполнение свойства б) проверяется непосредственно:

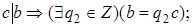
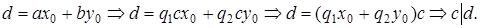
Рассмотрим теперь расширенный алгоритм Евклида для нахождения линейного представления наибольшего общего делителя 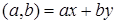 . Значения х и у вычисляются в серии шагов, в каждом из которых мы выражаем а i (вычисленное в процессе работы алгоритма Евклида) в форме
. Значения х и у вычисляются в серии шагов, в каждом из которых мы выражаем а i (вычисленное в процессе работы алгоритма Евклида) в форме 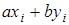 . А именно, рассмотрим последовательность
. А именно, рассмотрим последовательность
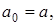
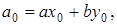
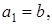
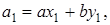
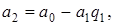
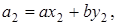

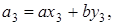
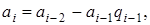
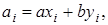
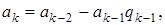
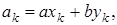
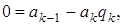
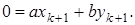
В левом столбце алгоритма записана последовательность делений, которая получается в результате работы алгоритма Евклида и которая разрешена относительно остатков. Согласно теореме Ламе (1844 г.) число делений, которое необходимо выполнить для нахождения (а, b), не превосходит числа цифр в меньшем из чисел а и b, умноженного на 5 (оценка наихудшего случая для алгоритма Евклида). Теорема Ламе доказывается на основе последовательности Фибоначчи.
Там же доказывается, что время выполнения алгоритма Евклида оценивается равенством 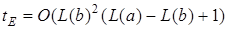 , где L(a) и L(b) – число цифр в а и b соответственно. В правом столбце этого алгоритма каждый остаток выражен через
, где L(a) и L(b) – число цифр в а и b соответственно. В правом столбце этого алгоритма каждый остаток выражен через 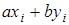 . Надо вычислить
. Надо вычислить 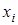 и
и 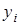 . Очевидно, что
. Очевидно, что 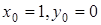 и
и  . Сравнивая обе части на i-м шаге, получим
. Сравнивая обе части на i-м шаге, получим
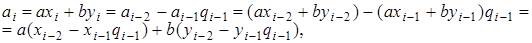
откуда получается следующая индуктивная процедура вычисления  и
и
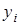 :
: 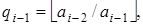

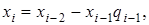
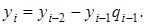
Пример. Применим расширенный алгоритм Евклида к числам а = 342, b = 612. Весь алгоритм представим в виде следующей таблицы.
Расширенный алгоритм Евклида
| Номер итерации | q | A0 | a1 | x0 | x1 | Y0 | y1 |
| 0 | - | 342 | 612 | 1 | 0 | 0 | 1 |
| 1 | 0 | 612 | 342 | 0 | 1 | 1 | 0 |
| 2 | 1 | 342 | 270 | 1 | -1 | 0 | 1 |
| 3 | 1 | 270 | 72 | -1 | 2 | 1 | -1 |
| 4 | 3 | 72 | 54 | 2 | -7 | -1 | 4 |
| 5 | 1 | 54 | 18 | -7 | 9 | 4 | -5 |
| 6 | 3 | 18 | 0 | 9 | -34 | -5 | 19 |
Заметим, что равенство 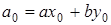 выполняется на каждом шаге итерации. Алгоритм выдаёт d = 18, x = 9, y = -5 и тогда 18=342∙9 + 612∙(-5).
выполняется на каждом шаге итерации. Алгоритм выдаёт d = 18, x = 9, y = -5 и тогда 18=342∙9 + 612∙(-5).
Дата добавления: 2019-07-15; просмотров: 309; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
