Теоремы Эйлера и Ферма, их роль в вычислении мультипликативных обратных элементов по данному модулю
Вернёмся теперь к вопросу о мультипликативных обратных элементах в фактор-кольце Zp.
Теорема. Пусть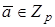 
, тогда класс 
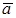имеет мультипликативный обратный элемент по модулю р тогда и только тогда, когда ( 
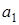, р) = 1.
Теорема. Характеристика λ конечного поля – простое число.
Рассмотрим два способа вычисления обратных мультипликативных элементов. Первый способ основан на рассмотренном выше алгоритме Евклида, второй – на теореме Эйлера.
Первый способ. Из условия (а, р) = 1 получаем ах + ру = 1 или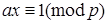 
и, следовательно, х – мультипликативный обратный к а по модулю р.
Второй способ. Предварительно напомним теорему Эйлера:
(а, р) = 1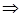 
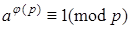, доказательство которой достаточно простое и мы его не приводим, так как его можно найти в любой книге по теории чисел. Частным случаем теоремы Эйлера является малая теорема Ферма.
Малая теорема Ферма. Если р – простое число и а – произвольное целое число, не делящееся на р, то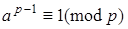 
.
Следствие. В кольце Zp классов вычетов по модулю р из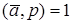 
следует, что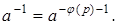 
Таким образом, для вычисления мультипликативного обратного к классу 
по модулю р в случае, когда 
, достаточно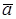 
возвести в степень k, где k = р – 2, если р – простое число, и 
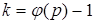в противном случае.
Ясно, что при таком методе вычисления мультипликативного обратного элемента задача сводится к цепочке умножений и делений с остатком на модуль р. Эта задача решается без особых трудностей, если наименьший положительный вычет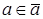 
, где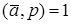 
, представлен в СОК. Однако возникает вопрос об эффективности этого метода. Другими словами, является ли 
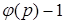наименьшим показателем степени, для которого 
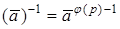? Оказывается, что нет.
|
|
|
Из китайской теореме об остатках следует следующее
Утверждение. Пусть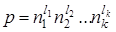 
- каноническое представление числа р. Тогда функция, которая каждому классу 
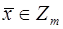ставит в соответствие кортеж 
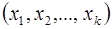, где 
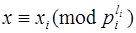для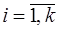 
, является кольцевым изоморфизмом кольца 
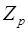класса вычетов по модулю р и кольца кортежей вида 
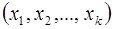, где 
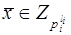для 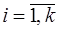. Более того, если обозначить через * любую из кольцевых операций + или · , то
Таким образом,
,
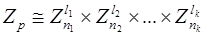т. е. кольцо классов вычетов по модулю р раскладывается в прямое произведение колец классов вычетов по модулям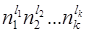 
. Это разложение колец индуцирует разложение групп их обратимых элементов:
.
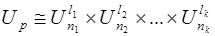Можно сделать вывод о том, что произвольное целое положительное число А, 0 < A < P, где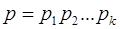 
и 
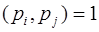для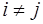 
, однозначно представимо своими наименьшими неотрицательными остатками по модулю 
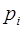, причём сложение (а, следовательно, и вычитание) и умножение выполняются покомпонентно.
Как следует из китайской теоремы об остатках, можно использовать любой соответствующий интервал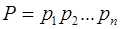 
целых чисел. Например, можно работать только с неотрицательными целыми числами, меньшими Р. С другой стороны, при выполнении операций сложения и вычитания, так же, как и умножения, обычно удобнее всего предположить, что все модули 
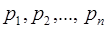являются нечётными целыми числами, так что и 
тоже нечётное, и можно работать с целыми числами из интервала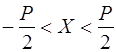 
, симметричного относительно нуля.
Дата добавления: 2019-07-15; просмотров: 177; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!