Задачи для самостоятельного решения

По данным индивидуального варианта выполните следующие задания.

1. Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений системы.

2. Определите метод оценки параметров модели.

3. Запишите приведенную форму модели.

Вариант 1

Модель денежного рынка:

где R – процентная ставка;

Y – ВВП;

М – денежная масса;

I – внутренние инвестиции;

t – текущий период.

Вариант 2

Модель Менгеса:

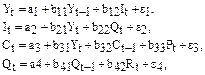
где Y – национальный доход;

С – расходы на личное потребление;

I – чистые инвестиции;

Q – валовая прибыль экономики;

Р – индекс стоимости жизни;

R – объем продукции промышленности;

t – текущий период;

t-1 – предыдущий период.

Вариант 3

Одна из версий модифицированной модели Кейнса имеет вид

где С – расходы на потребление;

Y – доход;

I – инвестиции;

G – государственные расходы;

t – текущий период;

t-1 – предыдущий период.

Вариант 4

Модель мультипликатора-акселератора:

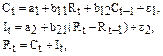
где С – расходы на потребление;

R – доход;

I – инвестиции;

t – текущий период;

t-1 – предыдущий период.

Вариант 5

Конъюнктурная модель имеет вид

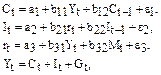
где С– расходы на потребление;

Y – ВВП;

I – инвестиции;

r – процентная ставка;

М – денежная масса;

G – государственные расходы;

t – текущий период;

t-1 – предыдущий период.

Вариант 6

Модель протекционизма Сальватора (упрощенная версия):

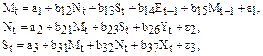
где М – доля импорта в ВВП; N – общее число прошений об освобождении от таможенных пошлин;

S – число удовлетворенных прошений об освобождении от таможенных пошлин;

Е – фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен,
и 0 – для всех остальных лет;

Y – реальный ВВП;

Х – реальный объем чистого экспорта;

t – текущий период,

t-1 – предыдущий период.

Вариант 7

Макроэкономическая модель (упрощенная версия модели Клейна):

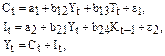
где С – потребление;

I – инвестиции;

Y – доход;

Т – налоги;

К – запас капитала;

t – текущий период;

t-1 – предыдущий период.

Вариант 8

Макроэкономическая модель экономики США (одна из версий):

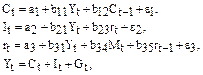
где С – потребление;

Y – ВВП;

I – инвестиции;

r – процентная ставка;

М – денежная масса;

G – государственные расходы;

t – текущий период;

t-1 – предыдущий период.

Вариант 9

Модель Кейнса (одна из версий):

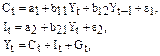
где С – потребление;

Y – ВВП;

I – валовые инвестиции;

G – государственные расходы;

t – текущий период;

t-l – предыдущий период.

Вариант 10

Модифицированная модель Кейнса:

где С – потребление;

Y – ВВП;

I – валовые инвестиции;

G – государственные расходы;

t – текущий период;

t-l – предыдущий период.

4. Временные ряды
в эконометрических исследованиях

Теоретическое введение

Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.

Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.

Каждый уровень временного ряда формируется из трендовой (Т), циклической (S) и случайной (Е) компонент.

Модели, в которых временной ряд представлен как сумма перечисленных компонент, – аддитивные модели, как произведение – мультипликативные модели временного ряда.

Аддитивная модель имеет вид: Y = T+ S + E.

M ультипликативная модель имеет вид: .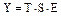

Построение аддитивной и мультипликативной моделей сводится к расчету значений Т, S и Е для каждого уровня ряда.

Построение модели включает следующие шаги:

1) выравнивание исходного ряда методом скользящей средней;

2) расчет значений сезонной компоненты S;

3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной (T+Е) или в мультипликативной ( 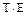) модели;

4) аналитическое выравнивание уровней (T+Е) или ( 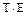) и расчет значений Т с использованием полученного уравнения тренда;

5) расчет полученных по модели значений (T+S) или ( );

6) расчет абсолютных и/или относительных ошибок.

Автокорреляция уровней ряда – это корреляционная зависимость между последовательными уровнями временного ряда:

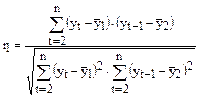где 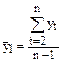; 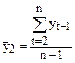– коэффициент автокорреляции уровней ряда первого порядка;

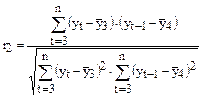где 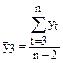; 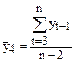– коэффициент автокорреляции уровней ряда второго порядка.

Формулы для расчета коэффициентов автокорреляции старших порядков легко получить из формулы линейного коэффициента корреляции.

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:

· линейная ;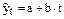

· гипербола ;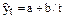

· экспонента ;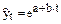

· степенная функция ;

· парабола второго и более высоких порядков

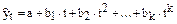Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время t = 1, 2, ..., n, а в качестве зависимой переменной – фактические уровни временного ряда у_t. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации .

При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.

Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например 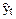и , и 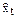расчет отклонений от трендов: и . Для дальнейшего анализа используют не исходные данные, а отклонения от тренда.

Метод последовательных разностей заключается в следующем: если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями:

;

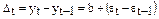если параболический тренд – вторыми разностями:

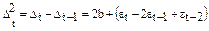В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.

Модель, включающая фактор времени, имеет вид

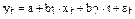Параметры а и b этой модели определяются обычным МНК.

Автокорреляция в остатках — корреляционная зависимость между значениями остатков e_t, за текущий и предыдущие моменты времени.

Для определения автокорреляции остатков используют критерий Дарбина - Уотсона и расчет величины:

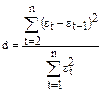, 0£d£4.

Коэффициент автокорреляции остатков первого порядка определяется по формуле

, .

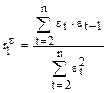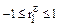Критерий Дарбина - Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением

Эконометрические модели, содержащие не только текущие, но и лаговые значения факторных переменных, называются моделями с распределенным лагом.

Модель с распределенным лагом в предположении, что максимальная величина лага конечна, имеет вид

Коэффициент регрессии b₀ при переменной х_t, характеризует среднее абсолютное изменение у_t, при изменении x_t на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.

В момент (t+1) воздействие факторной переменной х, на результат у_t составит (b₀+b₁) условных единиц; в момент времени (t+2) воздействие можно охарактеризовать суммой (b₀+b₁+b₂) и т.д. Эти суммы называют промежуточными мультипликаторами. Для максимального лага (t+l) воздействие фактора на результат описывается суммой (b₀+b₁+…+b_l=b), которая называется долгосрочным мультипликатором.

Величины

b_j=b_j/b, j=0,1,…,l

называются относительными коэффициентами модели с распределенным лагом. Если все коэффициенты b_j имеют одинаковые знаки, то для любого j

0<b_j<1 и .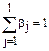

Величинa среднего лага модели множественной регрессии определяется по формуле средней арифметической взвешенной:

и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент t.

Медианный лаг – это период, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат:

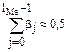
где l_Me – медианный лаг.

Оценку параметров моделей с распределенными лагами можно проводить согласно одному из двух методов: методу Койка или методу Алмон.

В распределении Койка делается предположение, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:

, l=0,1,2,…, 0<l<1.

Уравнение регрессии преобразуется к виду

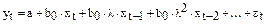После несложных преобразований получаем уравнение, оценки параметров которого приводят к оценкам параметров исходного уравнения.

В методе Алмон предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному распределению:

Уравнение регрессии примет вид

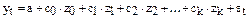где 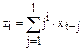, i=1,…,k; j=1,…,p.

Расчет параметров модели с распределенным лагом методом Алмон проводится по следующей схеме:

1) устанавливается максимальная величина лага l;

2) определяется степень полинома k, описывающего структуру лага;

3) рассчитываются значения переменных z₀,...,z_k;

4) определяются параметры уравнения линейной регрессии у_t от z_i;

5) рассчитываются параметры исходной модели с распределенным лагом.

Модели, содержащие в качестве факторов лаговые значения зависимой переменной, называются моделями авторегрессии, например:

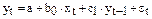Как и в модели с распределенным лагом, b₀ в этой модели характеризует краткосрочное изменение у_t под воздействием изменения х_t
на 1 ед. Долгосрочный мультипликатор в модели авторегрессии рассчитывается как сумма краткосрочного и промежуточных мультипликаторов:

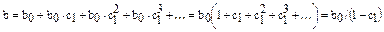Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.

Решение типовой задачи

Постановка задачи

Имеются следующие данные о величине дохода на одного члена семьи и расхода на товар А (таблица 4.1).

Таблица 4.1. Исходные данные задачи

Показатель	1985 г.	1986 г.	1987 г.	1988 г.	1989 г.	1990 г.
Расходы на товар А, руб.	30	35	39	44	50	53
Доход на одного члена семьи, % к 1985 г.	100	103	105	109	115	118

Требуется:

1. Определить ежегодные абсолютные приросты доходов и расходов и сделать выводы о тенденции развития каждого ряда.

2. Перечислить основные пути устранения тенденции для построения модели спроса на товар А в зависимости от дохода.

3. Построить линейную модель спроса, используя первые разности уровней исходных динамических рядов.

4. Пояснить экономический смысл коэффициента регрессии.

5. Построить линейную модель спроса на товар А, включив в нее фактор времени. Интерпретировать полученные параметры.

Решение задачи

1. Обозначим расходы на товар А через у, а доходы одного члена семьи – через х. Ежегодные абсолютные приросты определяются по формулам: , .

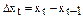Расчеты можно оформить в виде таблицы (таблица 4.2).

Таблица 4.2. Расчет абсолютных приростов

y_t	Dy_t	x_t	Dx_t
30		100
35	5	103	3
39	4	105	2
44	5	109	4
50	6	115	6
53	3	118	3

Значения Dу не имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда (линейной тенденции). Аналогичный вывод можно сделать и по ряду х: абсолютные приросты не имеют систематической направленности, они примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией.

2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар А в зависимости от дохода необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, т.е. Dу=f(Dх), если ряды динамики характеризуются линейной тенденцией.

Другой возможный путь учета тенденции при построении моделей – найти по каждому ряду уравнение тренда:

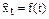
и отклонения от него:

; .

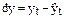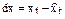Далее модель строится по отклонениям от тренда: dy=f(dx).

При построении эконометрических моделей чаще используется другой путь учета тенденции – включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельного фактора включается время, т.е. .

3. Модель имеет вид

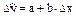Для определения параметров а и b применяется МНК. Система нормальных уравнений следующая:

Применительно к нашим данным имеем

Решая эту систему, получим:

а = 2,565 и b = 0,565,

откуда модель имеет вид

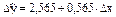4. Коэффициент регрессии b = 0,565 руб. Он означает, что с ростом прироста душевого дохода на 1%-ный пункт расходы на товар А увеличиваются со средним ускорением, равным 0,565 руб.

5. Модель имеет вид

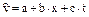Применяя МНК, получим систему нормальных уравнений:

Расчеты оформим в виде таблицы. 4.3.

Таблица 4.3. Расчетные данные

t	y	x	yx	y_t	x_t	x²	t²
1	30	100	3000	30	100	10000	1
2	35	103	3605	70	206	10609	4
3	39	105	4095	117	315	11025	9
4	44	109	4796	176	436	11881	16
5	50	115	5750	250	575	13225	25
6	53	118	6254	318	708	13924	36
21	251	650	27500	961	2340	70664	91

Система уравнений примет вид

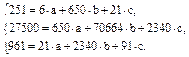
Решая ее, получим

а = –5,42; b = 0,322; с = 3,516.

Уравнение регрессии имеет вид

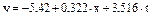Параметр b = 0,322 фиксирует силу связи у и х. Его величина означает, что с ростом дохода на одного члена семьи на 1%-ный пункт при условии неизменной тенденции расходы на товар А возрастают в среднем на 0,322 руб. Параметр с = 3,516 характеризует среднегодовой абсолютный прирост расходов на товар А под воздействием прочих факторов при условии неизменного дохода.

Дата добавления: 2019-02-26; просмотров: 289; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 Следующая ⇒

Мы поможем в написании ваших работ!