Миноры к-го порядка матрицы. Связь с рангом матрицы. Метод окаймляющих миноров

Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.

В матрице 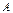размером вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы -го порядка, где . Определители таких подматриц называются минорами 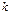-го порядка матрицы .

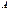Например, из матриц 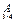можно получить подматрицы 1, 2 и 3-го порядка.

Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: или .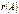

Из определения следует:

1) Ранг матрицы 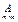не превосходит меньшего из ее размеров, т.е. .

2) 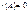тогда и только тогда, когда все элементы матрицы равны нулю, т.е. .

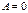3) Для квадратной матрицы n-го порядка тогда и только тогда, когда матрица - невырожденная.

Поскольку непосредственный перебор всех возможных миноров матрицы , начиная с наибольшего размера, затруднителен (трудоемок), то пользуются элементарными преобразованиями матрицы, сохраняющими ранг матрицы.

Определение ранга ч-з минор. Метод окаймляющих миноров.

Рангом матрицы называется наибольший порядок минора, отличного от нуля.

Отсюда – метод окаймляющих миноров.

Утверждение:

Определитель кВ матрицы =0 в том и только том случае, если между его строками есть линейная зависимость.

Метод окаймляющих миноров.

В матрице находим элемент, не равный нулю. Если такого нет, то определитель = 0, и rang = 0. Добавляем строку к столбец к элементу, не равному 0, получаем окаймляющие миноры 2-го порядка, среди них ищем миноры, не = 0, Если такого нет, то rang=1. Если есть, то ищем окаймляющие миноры 3-го порядка и т.д. Порядок старшего минора, не =0 и есть ранг матрицы.

Пример.

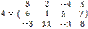
Rang(A) = 3

Системы линейных алгебраических уравнений

1. Системы линейных алгебраических уравнений. ~~Их равносильность~~. Элементарные преобразования. Метод Гаусса решения систем линейных уравнений.

Система трех линейных уравнений с тремя неизвестными 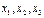имеет вид

(4)

где - коэффициенты системы, - свободные члены . Определитель третьего порядка Δ, составленный из коэффициентов при неизвестных, называется определителем системы.

Метод Гаусса.

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

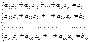
Разделим обе части 1–го уравнения на a₁₁ ¹ 0, затем:

1) умножим на а₂₁ и вычтем из второго уравнения

2) умножим на а₃₁ и вычтем из третьего уравнения

Получим:

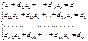, где d ₁ _j = a ₁ _j / a ₁₁ , j = 2, 3, …, n +1.

d_ij = a_ij – a_i1d_1j i = 2, 3, … , n; j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

Дата добавления: 2019-02-22; просмотров: 253; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 Следующая ⇒

Мы поможем в написании ваших работ!