Матрицы. Определение. Операции над матрицами, их свойства
Комплексные числа
1. Определение комплексного числа. Операции над комплексными числами, их свойства. Геометрическая интерпретация комплексных чисел.
1°. Определение. Алгебраическая форма записи.
Определение 1. Комплексными числами называются упорядоченные пары  действительных чисел
действительных чисел 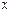 и
и 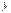 , если для них определены понятие равенства, операции сложения и умножения, удовлетворяющие следующим аксиомам:
, если для них определены понятие равенства, операции сложения и умножения, удовлетворяющие следующим аксиомам:
1°. Два числа 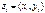 и
и 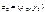 равны тогда и только тогда, когда
равны тогда и только тогда, когда 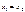 ,
, 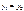 , т.е.
, т.е.
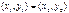 Û Û  , , 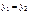 .(1) .(1)
|
2°. Суммой комплексных чисел  и
и 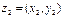 называется число, обозначаемое
называется число, обозначаемое 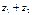 и равное
и равное  , т.е.
, т.е.
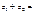 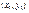 + + 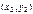 = = 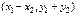 .(2) .(2)
|
3°. Произведением комплексных чисел 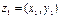 и
и 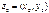 называется число, обозначаемое
называется число, обозначаемое 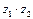 и равное
и равное 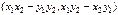 , т.е.
, т.е.
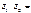 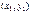 ∙ ∙ 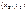 = = 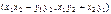 .(3) .(3)
|
Множество комплексных чисел обозначается С. 
Формулы (2),(3) для чисел вида 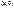 принимают вид
принимают вид
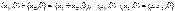 ,
,
откуда следует, что операции сложения и умножения для чисел вида  совпадают со сложением и умножением для вещественных чисел Þ комплексное число вида
совпадают со сложением и умножением для вещественных чисел Þ комплексное число вида  отождествляется с вещественным числом
отождествляется с вещественным числом 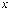 .
.
Комплексное число 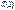 называется мнимой единицей и обозначается
называется мнимой единицей и обозначается 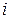 , т.е.
, т.е. 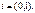 Тогда из (3) Þ
Тогда из (3) Þ 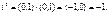 .
.
Из (2),(3) Þ что 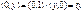 и значит
и значит

|
Выражение (4) называется алгебраической формой записи комплексного числа.
В алгебраической форме записи операции сложения и умножения принимают вид:
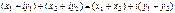
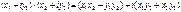 .
.
Комплексное число обозначают 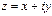 ,
, 
 – вещественная часть,
– вещественная часть,  – мнимая часть,
– мнимая часть,  – чисто мнимое число. Обозначение
– чисто мнимое число. Обозначение  ,
, 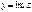 .
.
|
|
|
Определение 2. Комплексное число 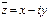 называется сопряженным с комплексным числом
называется сопряженным с комплексным числом 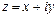 .
.
Свойства комплексного сопряжения.
1°. 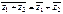 .
.
2°. 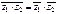 .
.
3°. Если 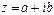 , то
, то 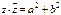 .
.
4°. 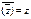 .
.
5°.  – вещественное число.
– вещественное число.
Доказательство проводится непосредственным вычислением.
Определение 3. Число 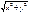 называется модулем комплексного числа
называется модулем комплексного числа 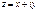 и обозначается
и обозначается  .
.
Очевидно, что 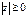 , причем
, причем 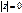

 . Также очевидны формулы:
. Также очевидны формулы: 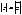 и
и 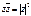 .
.
2°. Свойства операций сложения и умножения.
1°. Коммутативность: 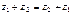 ,
,  .
.
2°. Ассоциативность: 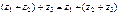 ,
, 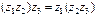 .
.
3°. Дистрибутивность: 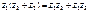 .
.
Доказательство 1° - 3° проводится непосредственными вычислениями на основе аналогичных свойств для вещественных чисел.
4°. 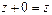 ,
, 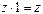 .
.
5°. 
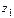 ,
, 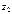
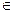 C
C 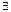 !
! 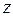 , удовлетворяющее уравнению
, удовлетворяющее уравнению  . Такое
. Такое
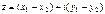 .
.
6°. 
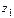 ,
, 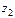
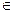 C,
C, 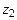
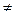 0,
0, 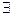 !
! 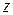 :
:  . Такое
. Такое 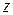 находится умножением уравнения на
находится умножением уравнения на 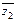
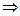

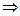
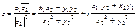 .
.
Пример. Представим комплексное число 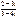 в алгебраической форме. Для этого умножим числитель и знаменатель дроби на число, сопряженное знаменателю. Имеем:
в алгебраической форме. Для этого умножим числитель и знаменатель дроби на число, сопряженное знаменателю. Имеем: 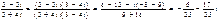
3°. Геометрическая интерпретация комплексных чисел. Тригонометрическая и показательная форма записи комплексного числа.
Пусть на плоскости задана прямоугольная система координат. Тогда 
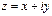
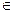 C можно поставить в соответствие точку на плоскости с координатами
C можно поставить в соответствие точку на плоскости с координатами 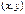 . Очевидно, что такое соответствие является взаимно однозначным. При этом действительные числа лежат на оси абсцисс, а чисто мнимые − на оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат − мнимой осью. Плоскость, на которой лежат комплексные числа, называется комплексной плоскостью.
. Очевидно, что такое соответствие является взаимно однозначным. При этом действительные числа лежат на оси абсцисс, а чисто мнимые − на оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат − мнимой осью. Плоскость, на которой лежат комплексные числа, называется комплексной плоскостью.
|
|
|
Отметим, что 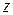 и
и 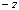 симметричны относительно оси Oy, а
симметричны относительно оси Oy, а 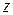 и
и 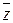 симметричны относительно Ox.
симметричны относительно Ox.
Каждому комплексному числу (т.е. каждой точке на плоскости) можно поставить в соответствие вектор с началом в точке O и концом в точке  . Соответствие между векторами и комплексными числами является взаимно однозначным. Поэтому вектор, соответствующий комплексному числу
. Соответствие между векторами и комплексными числами является взаимно однозначным. Поэтому вектор, соответствующий комплексному числу 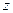 , обозначается той же буквой
, обозначается той же буквой 
Длина вектора 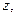 соответствующего комплексному числу
соответствующего комплексному числу 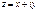 , равна
, равна 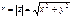 , причем
, причем  ,
, 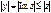 .
.
С помощью векторной интерпретации можно видеть, что вектор 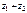 − сумма векторов
− сумма векторов  и
и 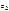 , а
, а 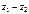 − сумма векторов
− сумма векторов  и
и 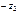 . Поэтому справедливо неравенство:
. Поэтому справедливо неравенство:  .
.
|
|
|
Наряду с длиной 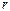 вектора
вектора  введем в рассмотрение угол
введем в рассмотрение угол 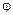 между вектором
между вектором  и осью Ox, отсчитываемый от положительного направления оси Ox: если отсчет ведется против часовой стрелки, то знак величина угла рассматривается положительной, если по часовой стрелке – то отрицательной. Этот угол называется аргументом комплексного числа и обозначается
и осью Ox, отсчитываемый от положительного направления оси Ox: если отсчет ведется против часовой стрелки, то знак величина угла рассматривается положительной, если по часовой стрелке – то отрицательной. Этот угол называется аргументом комплексного числа и обозначается 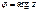 . Угол
. Угол 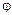 определяется не однозначно, а с точностью
определяется не однозначно, а с точностью 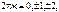 … . Для
… . Для 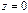 аргумент не определяется.
аргумент не определяется.
При этом
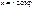 , , 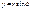 . .
|
Следовательно, любое комплексное число  можно представить в виде
можно представить в виде
 . .
|
Формулы (6) задают так называемую тригонометрическую форму записи комплексного числа.
Из (5) следует, что если 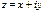 и
и 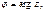 то
то
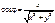 , ,  . .
|
Из (5) 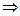 что по
что по  и
и 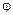 комплексное число определяется однозначно. Обратное неверно: а именно, по комплексному числу
комплексное число определяется однозначно. Обратное неверно: а именно, по комплексному числу 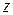 его модуль
его модуль  находится однозначно, а аргумент
находится однозначно, а аргумент 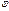 , в силу (7), − с точностью
, в силу (7), − с точностью 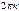 . Также из (7) следует, что аргумент
. Также из (7) следует, что аргумент 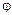 может быть найден как решение уравнения
может быть найден как решение уравнения

Однако не все решения этого уравнения являются решениями (7).
Среди всех значений аргумента комплексного числа выбирается одно, которое называется главным значением аргумента и обозначается  . Обычно главное значение аргумента выбирается либо в интервале
. Обычно главное значение аргумента выбирается либо в интервале 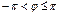 , либо в интервале
, либо в интервале 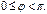
|
|
|
В тригонометрической форме удобно производить операции умножения и деления.
Теорема 1. Модуль произведения комплексных чисел 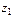 и
и 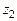 равен произведению модулей, а аргумент – сумме аргументов, т.е.
равен произведению модулей, а аргумент – сумме аргументов, т.е.
 , а
, а 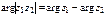 .
.
Аналогично
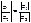 ,
,  .
.
Доказательство.Пусть 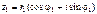 ,
, 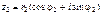 .Тогда непосредственным умножением получаем:
.Тогда непосредственным умножением получаем:
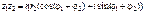 .
.
Аналогично
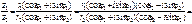
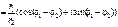
Следствие (формула Муавра). Для 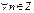 справедлива формула Муавра
справедлива формула Муавра
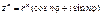 .
.
Пример. Пусть  Найдем геометрическое местоположение
Найдем геометрическое местоположение
точки 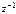 . Из теоремы 1 следует, что
. Из теоремы 1 следует, что  .
.
Поэтому для ее построение необходимо вначале построить точку 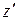 , являющуюся инверсией
, являющуюся инверсией 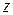 относительно единичной окружности, а затем найти точку, симметричную ей относительно оси Ox.
относительно единичной окружности, а затем найти точку, симметричную ей относительно оси Ox.
Пусть 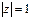 , т.е.
, т.е. 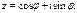 . Комплексное число
. Комплексное число 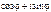 обозначается
обозначается  , т.е.
, т.е. 
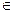 R справедлива формула Эйлера
R справедлива формула Эйлера

|
Так как  , то
, то 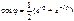 ,
, 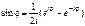 . Из теоремы 1
. Из теоремы 1 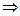 что с функцией
что с функцией 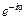 можно работать как с обычной показательной функцией, т.е. справедливы равенства
можно работать как с обычной показательной функцией, т.е. справедливы равенства
 ,
,  ,
, 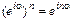 .
.
Из (8) 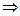 показательная форма записи комплексного числа
показательная форма записи комплексного числа
 , где
, где 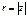 ,
, 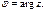
Пример.  .
.
4°. Корни n-ой степени из комплексного числа.
Рассмотрим уравнение
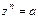 , ,  С, С, 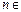 N . N .
|
Пусть 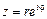 , а решение уравнения (9) ищется в виде
, а решение уравнения (9) ищется в виде 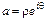 . Тогда (9) принимает вид
. Тогда (9) принимает вид 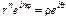 , откуда находим, что
, откуда находим, что  ,
, 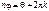 , т.е.
, т.е.
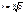 ,
,  ,
,  .
.
Таким образом, уравнение (9) имеет корни
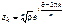 , , 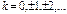 . .
|
Покажем, что среди (10) ровно 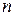 различных корней. Действительно,
различных корней. Действительно, 
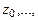
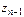 различны, т.к. их аргументы
различны, т.к. их аргументы  различны и отличаются меньше, чем на
различны и отличаются меньше, чем на 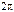 . Далее,
. Далее, 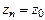 , т.к.
, т.к. 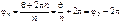 . Аналогично
. Аналогично 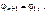 .
.
Таким образом, уравнение (9) при 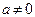 имеет ровно
имеет ровно 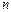 корней
корней 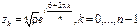 расположенных в вершинах правильного n-угольника, вписанного в окружность радиуса
расположенных в вершинах правильного n-угольника, вписанного в окружность радиуса 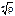 с центром в т. O.
с центром в т. O.
Таким образом, доказана
Теорема 2. Извлечение корня n-ой степени из комплексного числа 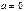 всегда возможно. Все значения корня n-ой степени из
всегда возможно. Все значения корня n-ой степени из 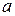 расположены в вершинах правильного n-угольника, вписанного в окружность с центром в нуле и радиуса
расположены в вершинах правильного n-угольника, вписанного в окружность с центром в нуле и радиуса 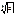 . При этом,
. При этом,
 .
.
Следствие. Корни n-ой степени из 1 выражаются формулой
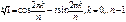 .
.
Произведение двух корней из 1 является корнем, 1 – корень n-ой степени из единицы, 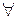 корня
корня 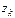
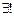
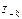 :
: 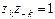 .
.
Матрицы
Матрицы. Определение. Операции над матрицами, их свойства
Определение. Матрицей размера 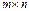 называется прямоугольная таблица, содержащая m строк и n столбцов.
называется прямоугольная таблица, содержащая m строк и n столбцов.
Матрицы широко применяются для описания экономических объектов и процессов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты.
Матрицы обозначают прописными (заглавными) буквами A , B , C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i - номер строки, j - номер столбца:
Виды матриц:
1) Матрица-строка: 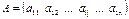 ;
;
2) Матрица-столбец:  ; 3) Нулевая матрица:
; 3) Нулевая матрица: 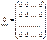 ;
;
4) Квадратная матрица – если 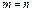 (например n = 2):
(например n = 2): 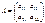 ;
;
5) Диагональная матрица (напр. 3-го порядка, где 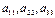 любые числа
любые числа 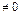 ):
): 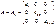 ;
;
6) Единичная матрица (например, 3-го порядка) 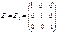
Операции над матрицами
1.Умножение матрицы на число.
Произведением матрицы A на число 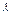 называется матрица
называется матрица 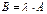 ,элементы которой
,элементы которой 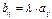 для
для 
Если 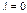 , то
, то 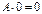 (нулевая матрица того же размера).
(нулевая матрица того же размера).
2.Сложение матриц.
Суммой матриц 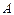 и
и 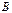 одинакового размера
одинакового размера 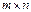 называется матрица
называется матрица  , элементы которой
, элементы которой  для
для 
Пример. Вычислить С = А + В, если 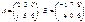 . Р е ш е н и е:
. Р е ш е н и е: 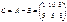 .
.
Вычитание матриц.
Разность матриц одинакового размера определяется как 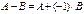 .
.
Умножение матриц.
Умножение матрицы 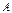 на матрицу
на матрицу 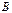 определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц
определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц 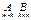 называется матрица
называется матрица 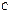 , каждый элемент которой
, каждый элемент которой 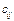 равен сумме произведений элементов
равен сумме произведений элементов 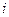 -ой строки матрицы
-ой строки матрицы 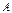 на соответствующие элементы
на соответствующие элементы 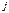 -го столбца матрицы
-го столбца матрицы 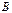 :
:
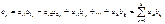 , где
, где 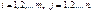
Пример. Вычислить произведение матриц 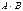 , где
, где 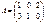 ,
, 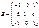 .
.
Р е ш е н и е.
Найдем размер матрицы произведения 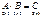 , следовательно, умножение возможно.
, следовательно, умножение возможно.
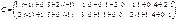 =
= 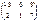 .
.
Дата добавления: 2019-02-22; просмотров: 128; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
