Свойства операций сложения и умножения матриц
1) 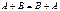 .
.
2) 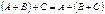 .
.
3) 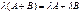 .
.
4) 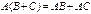 .
.
5) 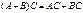
6) 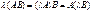
7) 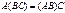
8) 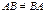 (в общем случае). Кроме того, если
(в общем случае). Кроме того, если 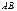 существует, то
существует, то 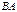 может вообще не существовать.
может вообще не существовать.
9) 
 , где
, где 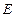 - единичная квадратная матрица.
- единичная квадратная матрица.
10) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. если 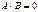 , то не следует, что
, то не следует, что 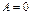 или
или 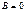 .
.
Пример. 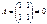 ,
, 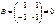 , но
, но 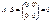 .
.
Возведение в степень.
Целой положительной степенью 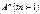 квадратной матрицы
квадратной матрицы 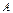 называют произведение
называют произведение 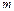 матриц, равных
матриц, равных 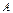 , т.е.
, т.е. 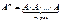 .
.
Транспонирование матриц.
Транспонирование матрицы есть переход матрицы 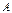 к матрице
к матрице 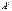 , в которой строки и столбцы поменялись местами с сохранением порядка.
, в которой строки и столбцы поменялись местами с сохранением порядка.
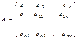 ,
, 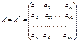 ,
,
т.е. если 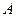 имеет размер
имеет размер 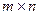 , то
, то 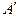 имеет размер
имеет размер 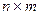 .
.
Свойства операции транспонирования.
1. 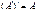 .
.
2. 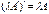 .
.
3. 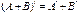
4. 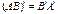
Обратная матрица. Определение. Свойства.
Обратная матрица
Для каждого числа 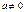 существует обратное число
существует обратное число 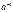 такое, что произведение
такое, что произведение 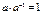 . Для квадратных матриц тоже вводится аналогичное понятие.
. Для квадратных матриц тоже вводится аналогичное понятие.
Определение. Матрица 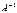 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 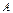 , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
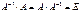 .
.
Только квадратная матрица может иметь обратную, однако не каждая квадратная матрица имеет обратную.
|
|
|
Определение. Матрица 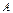 является невырожденной (неособенной), если
является невырожденной (неособенной), если  , в противном случае при
, в противном случае при  матрица
матрица 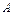 называется вырожденной (особенной).
называется вырожденной (особенной).
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 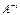 существует (и единственна) тогда и только тогда, когда исходная матрица является невырожденной (неособенной) и вычисляется по формуле
существует (и единственна) тогда и только тогда, когда исходная матрица является невырожденной (неособенной) и вычисляется по формуле
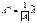 ,
,
где 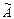 - присоединенная матрица, состоящая из алгебраических дополнений элементов транспонированной матрицы, т.е.
- присоединенная матрица, состоящая из алгебраических дополнений элементов транспонированной матрицы, т.е.  .
.
Необходимость. Пусть матрица 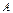 имеет обратную
имеет обратную 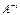 , т.е.
, т.е. 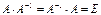 . По свойству 10 определителей имеем:
. По свойству 10 определителей имеем: 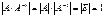 , т.е.
, т.е. 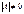 и
и 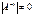 .
.
Достаточность. Пусть 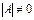 . Рассмотрим квадратную матрицу n-го порядка
. Рассмотрим квадратную матрицу n-го порядка 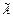 , называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы
, называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы 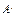 , транспонированной к
, транспонированной к 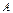 . Тогда элементы произведения матриц
. Тогда элементы произведения матриц 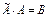 определяются по правилу умножения матриц. Поэтому матрица В является диагональной, элементы ее главной диагонали равны определителю исходной матрицы. А произведение
определяются по правилу умножения матриц. Поэтому матрица В является диагональной, элементы ее главной диагонали равны определителю исходной матрицы. А произведение 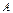 на
на 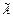 равно той же матрице В:
равно той же матрице В: 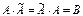 .
.
Единственность обратной матрицы. Предположим, что существуют еще матрицы 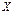 и
и 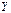 такие, что
такие, что 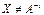 и
и 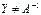 , где матрица
, где матрица 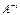 получена по формуле
получена по формуле 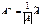 и выполняются равенства
и выполняются равенства 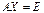 и
и 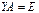 . Тогда, умножая на
. Тогда, умножая на 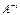 слева первое из них, получаем:
слева первое из них, получаем: 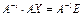 , откуда
, откуда 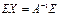 , т.е.
, т.е. 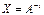 . Аналогично, умножая второе равенство на
. Аналогично, умножая второе равенство на 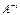 справа, получаем
справа, получаем 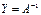 . Единственность доказана.
. Единственность доказана.
|
|
|
Свойства обратной матрицы:
§ 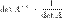 , где det обозначает определитель.
, где det обозначает определитель.
§ (AB) − 1 = B − 1A − 1 для любых двух обратимых матриц A и B.
§ (AT) − 1 = (A − 1)T где * T обозначает транспонированную матрицу.
§ (kA) − 1 = k − 1A − 1 для любого коэффициента 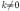 .
.
§ Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A - 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Перестановки.
Напомним, что если 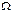 – множество из
– множество из 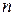 -элементов,
-элементов, 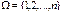 , то перестановкой степени
, то перестановкой степени 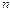 называется взаимнооднозначное отображение
называется взаимнооднозначное отображение  .
.  – множество всех перестановок степени
– множество всех перестановок степени 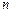 :
: 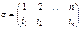 .
.
Лемма 1: Число различных перестановок равно 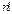
Лемма 2: Множество перестановок  образует группу относительно умножения, так что
образует группу относительно умножения, так что 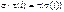 , обратный элемент получается сменой строк (Не коммутативная группа).
, обратный элемент получается сменой строк (Не коммутативная группа).
Отметим, что если в перестановке  поменять местами любые столбцы, то получится та же перестановка.
поменять местами любые столбцы, то получится та же перестановка.
Углубим проведенное ранее исследование:
|
|
|
Определение 1: Пусть  – перестановка степени
– перестановка степени 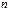 , пусть
, пусть 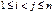 . Тогда пара
. Тогда пара 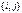 называется инверсией для
называется инверсией для  , если
, если 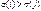 .
.
Перестановка  называется четной, если число инверсий для
называется четной, если число инверсий для  – четное, и перестановка нечетная, если число инверсий нечетное.
– четное, и перестановка нечетная, если число инверсий нечетное.
Знак перестановки  – это
– это  ,где
,где 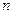 – число инверсий.
– число инверсий.
Обозначается  .
.
Итак, если  – четная, то
– четная, то 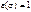 , и если
, и если  – нечетная, то
– нечетная, то 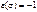 .
.
Пример:  . Пары
. Пары  . Их них подчеркнутые – инверсии. Таким образом,
. Их них подчеркнутые – инверсии. Таким образом,  , т.е.
, т.е.  – четная.
– четная.
Теорема 1:
1. Знак единичной перестановки  равен 1.
равен 1.
2. Если 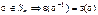 .
.
3. 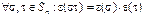 .
.
Доказательство: 1. В единичной перестановке инверсий нет  .
.
2. Пусть 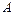 – множество инверсий относительно
– множество инверсий относительно 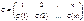 , а
, а 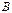 – множество инверсий относительно
– множество инверсий относительно 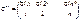 .
.
Легко видеть, что если 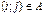 , то
, то 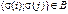 . Следовательно, между множествами
. Следовательно, между множествами 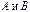 устанавливается взаимнооднозначное соответствие
устанавливается взаимнооднозначное соответствие
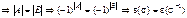 .
.
- Пусть
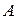 – множество инверсий относительно
– множество инверсий относительно  ,
,
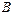 – множество инверсий относительно
– множество инверсий относительно  ,
,
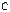 – множество инверсий относительно
– множество инверсий относительно 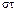 :
:  .
.
Тогда надо доказать, что  , т.е.
, т.е. 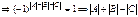 – четное число – это надо доказать.
– четное число – это надо доказать.
Пусть 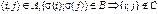 ,
,
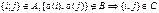 ,
,
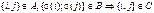 ,
,
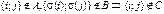 .
.
Введем следующее обозначение: пусть 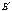 - это множество пар
- это множество пар 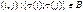 . Тогда справедлива следующая множественная схема:
. Тогда справедлива следующая множественная схема:
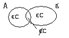 Между множествами
Между множествами 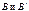 существует взаимнооднозначное соответствие
существует взаимнооднозначное соответствие 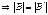 :
: 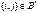
 .
.
|
|
|
Поэтому из картинки видно 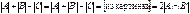 , т.е. четное число.
, т.е. четное число.
Следствие: 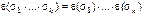 .
.
Обозначение: Пусть 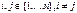 .
. 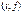 -перестановкой будем называть перестановку, при которой
-перестановкой будем называть перестановку, при которой 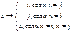
Определение 2: Перестановка вида 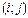 называется транспозицией. Они имеют вид
называется транспозицией. Они имеют вид 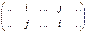 , где точками обозначены элементы, остающиеся на своих местах.
, где точками обозначены элементы, остающиеся на своих местах.
Теорема 2: Транспозиция – нечетная перестановка.
Доказательство: Вычислим число инверсий. Инверсиями являются пары 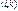 , где
, где 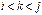 , пара
, пара 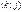 , где
, где 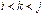 , и пара
, и пара 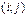 . Их всего будет
. Их всего будет 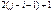 , т.е. нечетное число. ▄
, т.е. нечетное число. ▄
Замечание: Произведение 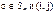 вида
вида 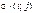 означает, что в нижней строке
означает, что в нижней строке 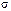 надо поменять местами
надо поменять местами 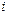 и
и 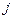 .
.
? Что означает 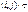 .
.
Пример 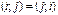 .
.
Теорема 3: Каждая перестановка является произведением конечного числа транспозиций.
Доказательство: Пусть 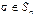 . Покажем, что нижняя строка
. Покажем, что нижняя строка 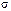 может быть получена из строки
может быть получена из строки 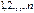 за конечное число шагов, каждый из которых состоит в том, что два числа меняются местами:
за конечное число шагов, каждый из которых состоит в том, что два числа меняются местами:
Пример: 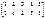
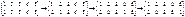
т.е. 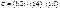 .
.
Аналогично в общем случае.
Пусть на втором шаге поменяются местами 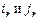 . Тогда ввиду замечания
. Тогда ввиду замечания 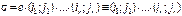 .
.
Упражнение: Каждая перестановка является произведением конечного числа транспозиций вида  .
.
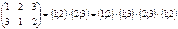 .
.
Теорема 4: При всех разложениях перестановки в произведения транспозиций, четность числа транспозиций одна и та же; она совпадает с четностью перестановки.
Доказательство: Пусть 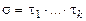 , где
, где 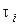 – транспозиция. Тогда знак
– транспозиция. Тогда знак 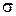 равен знаку произведения транспозиций
равен знаку произведения транспозиций 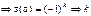 – четно, если
– четно, если 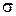 – четно.
– четно.
Дата добавления: 2019-02-22; просмотров: 167; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
