Моделирование непрерывных случайных величин. Метод обратной функции. Моделирование случайных величин с показательным и равномерным распределением.
Метод обратной функции.
Пусть имеется некоторая непрерывная СВ Х заданная функцией распределения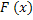 
. Можно доказать, что значения этой функции равномерно распределены в интервале (0;1). Поэтому между СВZ равномерно распределённые в том же интервале и функции распределения СВ Х существует взаимооднозначное соответствие, т.е. 
.
Отсюда следует, что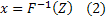 
где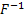 
- обратная функция
Следовательно если уравнение (1) имеет аналитическое решение, то для моделирования СВ Х можно использовать датчик случайных чисел, генерирующий величину Z, а затем, произвести расчет по формуле (2).
Моделирование СВ с показательным распределением.
Пусть имеется СВ Х с показательным распределением. Функция распределения имеет вид:
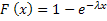
где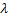 
– параметр распределения.
применив метод обратной функции получим:
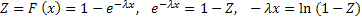
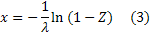
Учитывая что СВ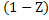 
также имеет равномерное распределение в интервале (0;1) соотношение (3) можно заменить соотношением:
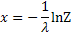
Моделирование СВ с равномерным распределением.
ДСЧ генерирует СВ с равномерным распределением в интервале (0;1). Если же нужно моделировать СВ с равномерным распределением в интервале (a;b), то можно воспользоваться снова методом обратной функции. Для рассматриваемого случая выражение (1) примет вид:
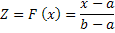
откуда
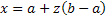
На практике применяется и другой способ задания равномерного распределения. Вместо границ интервала задаются среднее значение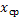 
СВ Х и величина интервала 
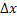. Тогда определение возможного значения СВ с равномерным распределением может быть произведено по формуле:
|
|
|
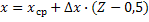
Моделирование случайных величин с нормальным распределением.
Метод обратной функции для нормального распределения не применим, так как после подстановки соответствующей функции распределения выражение (2) не имеет аналитического решения. Поэтому, в данном случае, применяется другой метод. Согласно центральной предельной теореме теории вероятности при сложении достаточно большого числа одинаково распределённых, независимых СВ получается СВ, имеющая нормальное распределение. Как показали исследования, уже при сложении более 10ти СВ с равномерным распределением в интервале (0;1) получается СВ, которая с точностью, достаточной для большинства практических задач, может считаться распределенной нормально.
Процедура розыгрыша нормально распределенной СВ состоит в следующем:
1. Сложим 12 СВ с равномерным распределением в интервале (0;1), т.е. составим сумму:
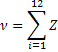
Использовав известные теоремы о сумме математических ожиданий и дисперсий независимых СВ можно установить, что в данном случае СВ V имеет следующие характеристики:
|
|
|
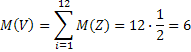
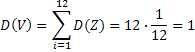
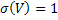
2. Нормируем и центрируем СВV, т.е. переходим к величине:
3. От нормированной и центрированной СВW перейдем к СВ Y с заданными параметрам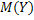и: 
и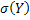 
по формуле:
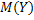– известное математическое ожидание,
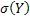– известное СКО.
Дата добавления: 2019-02-12; просмотров: 972; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!