Двойственная задача линейного программирования

Рассмотрим структуру и свойства двойственной задачи.

Каждой задаче линейного программирования определенным образом можно сопоставить некоторую другую задачу линейного программирования, которая называется двойственной или сопряженной по отношению к исходной или прямой задаче.

Пусть есть общая задача линейного программирования, состоящая в нахождении максимума целевой функции

F = c₁x₁+...+c_nx_n ® max (2.30)

при ограничениях

a₁₁x₁ + a₂₁x₁ + ... + a_1nx_n £ b₁,

.........,

a_k1x₁ + a_k2x₂ + ... + a_knx_n £ b_k,

a_k+1,1x₁ + a_k+1,2x₂ + ... + a_k+1,nx_n = b_k+1, (2.31)

.........,

a_m1x₁ + a_m2x₂ + ... + a_mnx_n = b_m,

x_j ³ 0 (j=1, ¼ ,l; l £ n).

Это прямая задача. Двойственной к этой задаче является задача, состоящая в нахождении минимума функции

F* = b₁y₁+b₂y₂+...+b_my_m (2.32’)

при ограничениях

a₁₁y₁+a₂₁y₁+...+a_m1y_m ³ c₁,

.........,

a_1ly₁+a_2ly₂+...+a_mly_m ³ c_l,

a_1,l+1y₁+a_2,l+1y₂+...+a_m,l+1y_m = c_l+1, (2.32”)

.........,

a_1ny₁+a_2ny₂+...+a_mny_m = c_n,

y_i ³ 0 (i=1, ¼ ,k; k £ m).

Двойственная задача по отношению к прямой составляется по следующим правилам:

1) если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот;

2) коэффициенты целевой функции прямой задачи c₁, c₂, ..., c_n становятся свободными членами ограничений двойственной задачи;

3) свободные члены ограничений прямой задачи b₁, b₂, ..., b_m становятся коэффициентами целевой функции двойственной задачи;

4) матрица ограничений двойственной задачи получается транспонированием матрицы ограничений прямой задачи;

5) число ограничений прямой задачи равно числу переменных двойственной задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи;

6) если переменная x_j прямой задачи может принимать только неотрицательные значения, то j-ое ограничение в двойственной задаче является неравенством вида больше или равно; если же переменная x_j может принимать как положительные, так и отрицательные значения, то j-ое ограничение в двойственной задаче – уравнение.

Двойственную задачу выгоднее решать, чем исходную прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений.

Двойственные пары задач подразделяются на симметричные и несимметричные. В симметричных задачах система ограничений записывается в виде неравенств и переменные могут принимать только неотрицательные значения.

Запишем правила перехода от прямой к двойственной задаче в матричном виде для симметричных и несимметричных задач (табл. 3).

Связь между оптимальными решениями прямой и двойственной задач устанавливают посредством следующих теорем теории двойственности.

Теорема 1. Если х₀ и u ₀ – допустимые решения прямой и двойственной задач соответственно, то значение целевой функции прямой задачи никогда не превышают значения целевой функции двойственной задачи.

Теорема 2. (основная теорема двойственности). Если х₀ и u ₀ – допустимые решения прямой и двойственной задач соответственно, и если выполняется равенство

C^T×x ₀ = u ₀ ^T×B, (2.33)

то х₀ и u ₀ – оптимальные решения пары двойственных задач.

Таблица 3

Для несимметричных задач
Прямая задача	Двойственная задача
F(x) = C^Tx ® max, Ax=B, x ³ 0.	G(u) = B^Tu ® min, A^Tu ³ C.
Для симметричных задач
F(x) = C^Tx ® max, Ax £ B, x ³ 0.	G(u) = B^Tu ® min, A^Tu ³ C, u ³ 0.

Транспортная задача

Существуют частные типы задач линейного программирования, которые, в силу особой своей структуры, допускают решение более простыми методами. Из них мы остановимся только на одной – так называемой "транспортной задаче" (ТЗ).

2.6.1. Формулировка транспортной задачи

Формулируется транспортная задача следующим образом: имеются m пунктов отправления (ПО) A₁, А₂, ..., А_m, в которых сосредоточены запасы каких-то однородных грузов в количестве соответственно а₁, а₂, ..., а_m, единиц. Имеются n пунктов назначения (ПН) В₁, В₂,..., В_n, подавших заявки соответственно на b₁, b₂, ..., b_n единиц груза.

Предполагается, что сумма всех заявок равна сумме всех запасов :

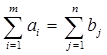. (2.34)

Условие (2.34) называется балансовым условием, а транспортная задача – задачей с правильным балансом.

Известны стоимости С_ij перевозки единицы груза от каждого пункта отправления A до каждого пункта назначения В. Задана матрица стоимостей С. Считается, что стоимость перевозки нескольких единиц груза пропорциональна их числу.

Требуется составить такой план перевозок, чтобы все заявки были выполнены, а общая стоимость всех перевозок минимальна.

Поставим эту задачу как задачу линейного программирования.

Обозначим через x_ij количество единиц груза, отправляемого из i-го ПО A_i в j-ый ПН B_j.

Совокупность чисел (х_ij) мы будем называть "планом перевозок", а сами величины x_ij –"перевозками". Эти неотрицательные переменные должны удовлетворять следующим условиям:

1. Суммарное количество груза, направляемого из каждого ПО во все ПН, должно быть равно запасу груза в данном пункте. Это даст нам m условий-равенств :

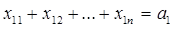: (2.35)

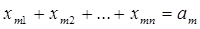или в общем виде

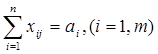. (2.36)

2. Суммарное количество груза, доставляемого в каждый ПН из всех ПО, должно быть равно заявке, поданной данным пунктом.

Это даст нам n условий-равенств :

: (2.37)

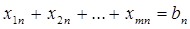или

. (2.38)

3. Суммарная стоимость всех перевозок, то есть сумма величин х_ij умноженных на соответствующие стоимости С_ij, должна быть минимальной:

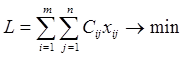, (2.39)

где знак двойной суммы означает, что суммирование производится по всем комбинациям индексов i и j, т. е. по всем парам ПО – ПН.

В такой формулировке это – задача линейного программирования с условиями-равенствами и минимизируемой целевой линейной функцией. Однако, транспортная задача имеет особенности, которые позволяют решить ее более простыми способами.

1. Все коэффициенты при переменных в ограничениях равны единице.

2. Значение имеет структура связей между переменными. Заметим, что условия-равенства не являются линейно независимыми, так как их правые части связаны условием (2.34). Число линейно независимых уравнений равно не m + n (числу уравнений), а (n + m –1). Общее число переменных в нашей задаче равно m × n.

Число свободных переменных k определится как разность между числом переменных и числом линейно независимых уравнений

k = m × n –( m + n –1)=( m –1)( n –1) . (2.40)

Так как транспортная задача является задачей линейного программирования, то ее оптимальное решение достигается в одной из опорных точек, в которой, по крайней мере, k переменных обращаются в нуль. Значит для оптимального плана ( m –1)( n –1) перевозок должны быть равны нулю.

Будем называть любой план перевозок допустимым, если он удовлетворяет условиям-равенствам (все заявки удовлетворены, все запасы исчерпаны).

Допустимый план будем называть опорным, если в нем отличны от нуля не более n + m – 1 базисных перевозок, а остальные перевозки равны нулю.

План будем называть оптимальным, если он, среди всех допустимых планов, приводит к минимальной суммарной стоимости перевозок.

В силу особой структуры ТЗ при ее решении не приходится переразрешать систему уравнений. Все операции по нахождению оптимального плана сводятся к манипуляциям непосредственно с таблицей, называемой транспортной (табл. 4). В ней в определенном порядке записаны условия транспортной задачи: перечень ПО и ПН, заявки и запасы, а также стоимости перевозок. По мере заполнения этой таблицы в ее клетках проставляются сами перевозки.

Транспортная таблица состоит из m строк и n столбцов. В правом верхнем углу каждой клетки ставятся стоимость перевозки единицы груза, а центр клетки остается свободным, чтобы помещать в нее саму перевозку.

Нахождение решения транспортной задачи заключается в преобразовании транспортной таблицы (табл. 4).

Таблица 4

ПО	ПН				Запас a_i
ПО	В ₁	В ₂	. . .	В _n	Запас a_i
А ₁	c₁₁	c₁₁	. . .	c_1n	a₁
А ₂	c₂₁	c₂₂	. . .	c_2n	a₂
. . .	. . .	. . .	. . .	. . .
А_m	c_m1	c_m2	. . .	c_mn	a_m
Заявки b_j	b₁	b₂	. . .	b_n	å b_j = å a_i

2.6.2. Нахождение опорного решения

В отличие от других задач линейного программирования с произвольными ограничениями и целевой функцией, транспортная задача всегда имеет решение, исходя из чисто физических соображений. Она должна иметь оптимальное решение, так как целевая функция ограничена снизу нулем.

Существует несколько методов нахождения опорного плана. Рассмотрим один из них, так называемый "метод северо-западного угла". Продемонстрируем его непосредственно на конкретном примере.

Пример

Имеется транспортная таблица (табл. 5).

Начнем заполнение транспортной таблицы с левого верхнего ("северо-западного") угла (табл. 6). Пункт B₁ подал заявку на 18 единиц груза; удовлетворим ее из запасов пункта А₁. После этого в нем остается еще 48 – 18 =30 единиц груза; отдадим из них 27 пункту B₂. Оставшиеся 3 единицы груза из запасов пункта A₁ отдадим пункту B₃. Запасы первого пункта исчерпаны. Заявка пункта B₃ еще не выполнена: 30 единиц груза отдаем за счет пункта A₂ (запасы его исчерпаны), недостающие 9 единиц – за счет пункта A₃. Заявку пункта B₄ выполняем из запасов пункта A₃, в котором остается еще 6 единиц, их отдаем пункту B₅, запасы пункта A₃ исчерпаны. Последние 20 единиц груза пункта A₄ отдаем пункту B₅.

Таблица 5

ПО	ПН					Запас a_i
ПО	В ₁	В ₂	В ₃	В ₄	В ₅	Запас a_i
А ₁	¹⁰	⁸	⁵	⁶	⁹	48
А ₂	⁶	⁷	⁸	⁶	⁵	30
А ₃	⁸	⁷	¹⁰	⁸	⁷	27
А₄	⁷	⁵	⁴	⁶	⁸	20
Заявки b_j	18	27	42	12	26	125

Таблица 6

ПО	ПН					Запас a_i
ПО	В ₁	В ₂	В ₃	В ₄	В ₅	Запас a_i
А ₁	18 ¹⁰	27 ⁸	3 ⁵	⁶	⁹	48
А ₂	⁶	⁷	30 ⁸	⁶	⁵	30
А ₃	⁸	⁷	9 ¹⁰	12 ⁸	6 ⁷	27
А₄	⁷	⁵	⁴	⁶	20 ⁸	20
Заявки b_j	18	27	42	12	26	125

Проверим, является ли этот план допустимым.

Да, потому что в нем сумма перевозок по строке равна запасу соответствующего пункта отправления, а сумма перевозок по столбцу – заявке соответствующего пункта назначения; значит, все заявки удовлетворены, все запасы израсходованы (сумма запасов равна сумме заявок и выражается числом 125, стоящим в правом нижнем углу табл. 5).

Здесь и в дальнейшем мы проставляем в таблице только отличные от нуля перевозки, а клетки, соответствующие нулевым перевозкам, оставляем "свободными". Проверим, является ли план перевозок опорным?

Дата добавления: 2019-02-12; просмотров: 415; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 Следующая ⇒

Мы поможем в написании ваших работ!