Прямые и обратные задачи исследования операций.

Детерминированные задачи

Задачи исследования операций делятся на две категории:

а) прямые;

б) обратные.

Прямые задачи отвечают на вопрос: что будет, если в заданных условиях мы примем какое-то решение х из X? В частности, чему будет равен, при данном решении х, выбранный показатель эффективности W (или же ряд таких показателей)?

Для решения такой задачи строится математическая модель, позволяющая выразить один или несколько показателей эффективности через заданные условия и элементы решения.

Обратные задачи отвечают на вопрос: как выбрать решение х для того, чтобы показатель эффективности W обратился в максимум?

Случай минимизации сводится к первому простым изменением знака .

Естественно, прямые задачи проще обратных. Очевидно также, что для решения обратной задачи, прежде всего надо уметь решать прямую задачу. Для некоторых типов операций прямая задача решается настолько просто, что ею специально не занимаются. Для других типов операций построение математических моделей и вычисление показателя (показателей) эффективности само по себе далеко не тривиально.

Остановимся несколько подробнее на обратных задачах. Если число возможных вариантов решения, образующих множество X, невелико, то можно вычислить величину W для каждого из них, сравнить между собой полученные значения и непосредственно указать один или несколько оптимальных вариантов, для которых W достигает максимума. Такой способ нахождения оптимального решения называется "простым перебором".

Однако, когда число возможных вариантов решения, образующих множество X, велико, поиск простым перебором затруднителен, а зачастую практически не возможен. В этих случаях применяются методы "направленного перебора".

Особенностью этих методов является то, что оптимальное решение находится путем последовательных "попыток" или "приближений", из которых каждое последующее приближает нас к искомому оптимальному.

Сформулируем задачу оптимизации решения (обратную задачу исследования операций) в общей форме.

Пусть имеется некоторая операция О, на успех которой мы можем в какой-то мере влиять, выбирая тем или другим способом решение х (напомним, что х – группа параметров). Пусть эффективность операции характеризуется одним показателем W Þ max.

Возьмем самый простой, так называемый детерминированный случай, когда все условия операции полностью известны заранее, т. е. не содержат неопределенности.

Тогда факторы, от которых зависит успех операции, делятся на две группы:

1) заданные, заранее известные факторы (условия выполнения операции), которые мы для краткости обозначим одной буквой b;

2) зависящие от нас элементы решения, образующие в своей совокупности решение х.

Заметим, что первая группа факторов содержит и ограничения, налагаемые на решение, т. е. определяет область возможных решений X.

Показатель эффективности W зависит от обеих групп факторов. Это мы запишем в виде формулы:

W=W(b, x). (1.3)

При рассмотрении формулы не надо забывать, что как х, так и b в общем случае – не числа, а совокупности чисел (векторы), функции и т. д. В числе заданных условий b обычно присутствуют ограничения, налагаемые на элементы решения, имеющие вид равенств или неравенств.

Будем считать, что вид зависимости (1.3) нам известен, т. е. прямая задача решена. Тогда обратная задача формулируется следующим образом.

При заданном комплексе условий b найти такое решение х = х*, которое обращает показатель эффективности W в максимум.

Этот максимум мы обозначим:

W* = max {W(b,x)}, (1.4)

x Î Х.

Для простоты в дальнейшем мы будем говорить просто о "максимуме" показателя, не оговаривая каждый раз, что может потребоваться обратить его в минимум.

Формула (1.4) читается так: W* есть максимальное значение W(b,x), взятое по всем решениям, входящим во множество возможных решений X.

Итак, перед нами – типичная математическая задача нахождения максимума функции или функционала. Напомним, что "функционалом" называется величина, зависящая от вида функции.

Мы рассмотрели обратную задачу исследования операций в детерминированном случае, когда показатель эффективности W зависит только от двух групп факторов: заданных, заранее известных b и элементов решения х. Реальные зада-

чи исследования операции чаще всего содержат помимо этих двух групп еще одну – неизвестные факторы, которые в совокупности мы обозначим одной буквой x. Итак, показатель эффективности W зависит от всех трех групп факторов:

W=W (b, x, x). (1.5)

Так как величина W зависит от неизвестных факторов x, то даже при заданных b и x она уже не может быть вычислена, остается неопределенной. Задача поиска оптимального решения тоже теряет определенность.

Переводя сказанное на математический язык, поставим перед собой следующую задачу: при заданных условиях b, с учетом неизвестных факторов x, найти такое решение х из X, которое, по возможности, обеспечивает максимальное значение показателя эффективности W.

Это уже другая, не чисто математическая задача. Наличие неопределенных факторов переводит задачу в новое качество: она превращается в задачу о выборе решения в условиях неопределенности.

Если условия операции неизвестны, мы не можем так же успешно оптимизировать решение, как мы это сделали бы, если бы располагали большей информацией. Поэтому любое решение, принятое в условиях неопределенности, хуже решения, принятого в заранее известных условиях.

Так как успех операции зависит от проявления случайных факторов x, то критерий эффективности W, приобретает вероятностный характер.

Для иллюстрации принципов выбора показателя эффективности вернемся к примерам 1 – 6 п. 1.1.

1. План снабжения предприятий. Задача операции – обеспечить снабжение предприятий сырьем при минимальных расходах на перевозки. Показатель эффективности R – суммарные расходы на перевозки сырья за единицу времени (R Þ min).

2. Постройка участка магистрали. Требуется так спланировать строительство, чтобы закончить его в минимально возможный срок. Естественным показателем эффективности было бы время завершения стройки, если бы оно не было связано со случайными факторами (отказами техники, задержки и выполнения отдельных работ). Поэтому в качестве показателя эффективности можно выбрать среднее ожидаемое время Т окончания стройки (Т Þ min).

3. Продажа сезонных товаров. В качестве показателя эффективности можно взять среднюю ожидаемую прибыль П от реализации товаров за сезон (П Þmax).

4. Противолодочный рейд. Так как рейд имеет вполне определенную цель А – уничтожение лодки, то в качестве показателя эффективности следует выбрать вероятность Р(А) того, что лодка будет уничтожена.

5. Выборочный контроль продукции. Естественный показатель эффективности – это средние ожидаемые расходы R на контроль за единицу времени, при условии, что система контроля обеспечивает заданный уровень качества, например, средний процент брака не выше заданного (R Þ min).

6. Медицинское обследование. В качестве показателя эффективности можно выбрать средний процент (долю) Q больных и носителей инфекции, которых удалось выявить (QÞ min).

Критерии эффективности

Какая бы форма критерия не использовалась, существуют общие требования, которым должен отвечать любой конкретный критерий эффективности.

Требования к критерию эффективности (W).

1) представительность, то есть критерий эффективности W должен отражать основную цель операции;

2) критичность и чувствительность к изменению исследуемых параметров;

3) максимальная простота, то есть зависимость от наиболее существенных параметров операции;

4) единственность (это требование желательное).

Несмотря на ряд существенных трудностей, связанных с неопределенностью, мы до сих пор рассматривали только самые простые случаи, когда ясен критерий, по которому производится оценка эффективности, и требуется обратить в максимум (минимум) один-единственный показатель W.

А когда идет речь о крупномасштабных, сложных операциях, затрагивающих разнообразные интересы их организаторов и общества в целом, то их эффективность, как правило, не может быть полностью охарактеризована с помощью одного-единственного показателя эффективности W. На помощь ему приходится привлекать другие, дополнительные. Такие задачи исследования операций называются многокритериальными.

Итак, типичным для крупномасштабной задачи исследования операций является многокритериальность – наличие ряда количественных показателей W₁, W₂, ..., W_n, одни из которых желательно обратить в максимум, другие – в минимум.

Существует несколько подходов к объединению частных критериев в один обобщенный критерий эффективности.

1. Наиболее распространенный способ составления "обобщенного" показателя эффективности – он представляет собой "взвешенную сумму" частных показателей, в которую каждый из них W, входит с каким-то весовым коэффициентом g, отражающим его важность:

W= g ₁ W₁+ g ₂ W₂+...+ g _n W_n , (1.6)

где g _i – положительные или отрицательные весовые коэффициенты частных критериев W_i (для тех показателей, которые желательно увеличить, веса берутся положительные, для тех показателей, которые желательно уменьшить – отрицательные).

Часто к условию (1.6) добавляется условие нормировки, требующее, чтобы сумма весовых коэффициентов:

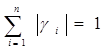. (1.7)

Определение весовых коэффициентов – трудоемкая задача. Ее решение достигается либо опросом экспертов, либо логическим анализом, либо статистическим моделированием.

2. Иногда (особенно при решении технико-экономических задач) обобщенный показатель имеет вид дроби:

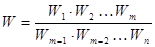, (1.8)

причем в числителе стоят все показатели, которые желательно максимизировать, а в знаменателе – те, которые желательно минимизировать.

Такой способ объединения нескольких показателей в один не может быть рекомендован: он основан на неявном допущении, что недостаток в одном показателе всегда может быть скомпенсирован за счет другого.

3. Иногда в задаче с несколькими показателями удается выделить главный критерий эффективности , который стремятся обратить в экстремум. Остальные критерии в этом случае переводятся в разряд ограничений вида:

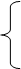W₂ ³ w ₂ ; … ; W_m ³ w _m ; (1.9)

W_m+1 £ w _m+1 ; … ; W_n £ w _n .

4. Существует еще один путь построения компромиссного решения, более сложный, но вместе с тем, более объективный, который можно назвать "методом последовательных уступок": показатели W₁,W₂,...,W_n располагаются в порядке убывающей важности. При этом в определении порядка расположения критериев

может присутствовать субъективизм, но его можно уменьшить с помощью экспертных опросов специалистов.

Сначала ищется решение, обращающее в максимум первый (важнейший) показатель W₁=W₁*. Затем назначается, исходя из практических соображений, с учетом малой точности, с которой нам известны исходные данные, некоторая "уступка", которую мы согласны сделать для того, чтобы максимизировать второй показатель W₂. Наложим на показатель W₁ ограничение: потребуем, чтобы он был не меньше, чем W₁*, и при этом ограничении ищем решение, обращающее в максимум W₂. Далее снова назначим "уступку" в W₂, ценой которой можно максимизировать W₃, и т. д. Такой способ построения компромиссного решения хорош тем, что здесь сразу видно, ценой какой "уступки" в одном показателе приобретается выигрыш в другом и какова величина этого выигрыша.

5. Очень сложно выбрать критерий, который должен характеризовать достижение цели операции, когда последняя протекает либо в условиях неопределенности, либо в условиях сознательного противодействия выполнению наших задач (например, при проведении боевых действий – противодействие противника). Для оценки эффективности операции в этих случаях разработаны специальные критерии эффективности в условиях неопределенности.

Пусть отыскивается наилучшее решение Х, при котором максимизируется критерий эффективности W. На критерий W оказывают влияние условия проведения операции, значения которых не известны.

В этом случае необходимо задаться возможными значениями А, т.е., A ₁ , A ₂ , …, A_n ; возможными значениями Х, т.е. X ₁ , X ₂ , …, X_m и для всех значений комбинаций X_i A_j рассчитать критерий K_ij . Результаты расчетов удобно свести в таблицу (табл.1).

Тогда, обобщенный критерий эффективности операции, используя данные таблицы, можно составить различными методами.

а) критерий Лапласа

Этот критерий используется, если все условия A_j считаются равновероятными. Критерий записывается в следующем виде:

W _л = 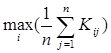. (1.10)

Таблица 1

X	A
X	A ₁	A ₂	A ₃	…	A_n
X ₁	K ₁₁	K ₁₂	K ₁₃	…	K ₁ _n
X ₂	K ₂₁	K ₂₂	K ₂₃	…	K _2n
…	…	…	…	…	…
X_m	K_m ₁	K_m ₂	K_m ₃	…	K_mn

Исходя из этого критерия, определяют оптимальное решение, при котором имеет место максимум критерия Лапласа.

Если известны вероятности появления условий A_j, то есть P_j(A_j), то критерий Лапласа приобретает вид

W _л = 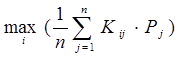. (1.11)

б) критерий Вальда(или максиминный критерий, или критерий осторожного поведения)

Оптимальное решение – то, которое дает вполне определенный гарантированный выигрыш при наихудших условиях:

W_B = 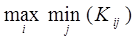. (1.12)

Применяя этот критерий всегда ориентируются на наихудшие условия. Этот критерий целесообразно применять в случае сознательного противодействия достижению цели данной операции.

в) критерий Гурвица (или критерий компромиссного поведения)

W _Г = 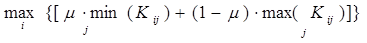, (1.13)

где m – "коэффициент пессимизма", выбираемый между нулем и единицей.

Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом.

При m = 1 критерий Гурвица превращается в пессимистический критерий Вальда, при m = 0 – в критерий крайнего оптимизма, при котором необходимо выбирать решение, приносящее наибольший выигрыш в самых благоприятных ситуациях.

Промежуточное значение m выбирается из субъективных соображений. Чем опаснее ситуация, тем m ближе к 1.

г) критерий Сэвиджа (или критерий минимаксного риска)

Этот критерий – крайне пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на выигрыш, а на риск.

Определяется отрицательная матрица потерь R = r_ij :

r_ij = K_ij– max K_ij. (1.14)

Величина r_ij измеряется разностью между фактически полученным результатом и результатом, который можно было бы получить, если бы условия проведения операции были точно известны.

К матрице потерь R применяется критерий Вальда. В результате имеем:

W_с = max min ( r _ij ). (1.15)

ⁱ ^j

Описанные случаи не исчерпывают всего многообразия принципов выбора критериев эффективности, однако, с помощью их комбинаций можно получить и более сложные варианты выбора обобщенного критерия.

Следует отметить еще одну особенность, которая часто объективно существует при решении вопроса о выборе критерия эффективности. Выше предполагалось, что критерий эффективности поддается, в принципе, физическому измерению, однако в ряде случаев не существует способов количественного измерения цели операции. Тогда приходится пользоваться приемом, называемым ранжированием (ранговым подходом). При этом критериям эффективности присваиваются оценки – ранги по заранее выбранной шкале: двухбалльной, пятибалльной и т.д.

Ранговый критерий имеет дискретную ограниченную область определения. В простейшем случае область содержит два значения ("да – нет", "хорошо – плохо", "ноль – один" и т.д.). Это может соответствовать, например, достижению или недостижению цели операции.

Ранг – это количественная оценка критерия эффективности, носящая субъективный характер, т.к. качественному признаку ставится в соответствие некоторое число. Ранговый подход имеет наибольшее распространение при проведении различных экспертных опросов.

Глава 2.

Линейное программирование

Постановка основной задачи

Линейного программирования

Задачи нахождения значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, носят общее название задач математического программирования. В самом общем случае они формулируются в следующем виде.

Найти max f ( x ₁ , …, x_n ) при ограничениях:

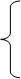g₁(x₁, …,x_n) £ b₁,

× × × × × × (2.1)

g_m(x₁, …,x_n) £ b_m ,

где f – целевая функция (показатель эффективности); x ₁ , …, x_n – варьируемые параметры; g ₁ , …, g_m – функции, которые задают ограничения на варьируемые параметры.

Трудности, возникающие при решении задач математического программирования, зависят:

а) от вида функциональной зависимости, связывающей функцию f с элементами решения;

б) от "размерности" задачи, т. е. от количества элементов решения;

в) от вида и количества ограничений, наложенных на элементы решения.

Среди задач математического программирования самыми простыми, и поэтому хорошо изученными, являются так называемые задачи линейного программирования.

Для таких задач характерны следующие особенности:

а) показатель эффективности (целевая функция) W линейно зависит от элементов решения x₁.,…, x _n;

б) ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно x₁.,…, x _n.

Любую задачу линейного программирования можно свети к стандартной форме, так называемой ²основной задаче линейного программирования² (ОЗЛП), которая формулируется следующим образом.

Найти неотрицательные значения переменных x₁,…, x _n, которые удовлетворяли бы системе линейных уравнений:

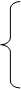a₁₁x₁+a₁₂x₂+ … +a_1nx_n=b₁,

a₂₁x₁+a₂₂x₂+ … +a_2nx_n=b₂,

× × × × × × × × (2.2)

a_m1x₁+a_m2x₂+ … +a_mnx_n=b_m

и обращали бы в максимум линейную функцию этих переменных:

L = C ₁ x ₁ + C ₂ x ₂ + … + C_nx_n ® max. (2.3)

Переход к основной задаче осуществляется по следующим правилам.

1. Если в задаче надо определить минимум целевой функции, то она легко сводится к классической, если просто изменить знак L на обратный (максимизировать не L, а L' = – L).

2. От любых условий-неравенств можно перейти к условиям-равенствам ценой введения некоторых новых "дополнительных" переменных.

Покажем, как это делается.

Пусть требуется найти неотрицательные значения переменных x₁,…, x _n, удовлетворяющие ограничениям-неравенствам:

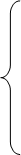a₁₁x₁+a₁₂x₂+ … +a_1nx_n ³ b₁,

a₂₁x₁+a₂₂x₂+ … +a_2nx_n ³ b₂,

× × × × × × × × (2.4)

a_k,1x₁+a_k,2x₂+ … +a_k,nx_n ³ b_k,

a_k+1,1x₁+a_k+1,2x₂+ … +a_k+1,nx_n=b_k+1,

× × × × × × × ×

a_m1x₁+a_m2x₂+ … + a_mnx_n = b_m .

В системе имеется k неравенств и m – k равенств, причем k может равняться m. Будем считать, что все ограничения линейно независимы, т.е. никакое из них нельзя представить в виде линейной комбинации других.

Чтобы перейти к системе равенств, вводятся новые неотрицательные добавочные переменные x_n ₊₁ , …, x_n ₊ _k, например:

x_n+1=a₁₁x₁+a₁₂x₂+ … +a_1nx_n–b₁ ³ 0. (2.5’)

Если в уравнении знак £ , то все переносим вправо:

x_n ₊ _k = b_k – ( a_k ₁ x ₁ + a_k ₂ x ₂ + … + a_knx_n ) ³ 0. (2.5”)

Тогда система примет вид:

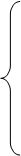a₁₁x₁+a₁₂x₂+ … +a_1nx_n–x_n+1=b₁,

a₂₁x₁+a₂₂x₂+ … +a_2nx_n–x_n+2=b₂,

× × × × × × × × (2.6)

a_k,1x₁+a_k,2x₂+ … +a_k,nx_n–x_n+k=b_k,

a_k+1,1x₁+a_k+1,2x₂+ … +a_k+1,nx_n=b_k+1,

a_m ₁ x ₁ + a_m ₂ x ₂ + … + a_mnx_n = b_m .

Тогда основная задача линейного программирования ставится так: найти такие неотрицательные значения переменных x₁, x₂, … x_n₊ _k, которые удовлетворяли

бы системе линейных уравнений (2.6) и обращали бы в максимум линейную функцию вида

L = C ₁ x ₁ + C ₂ x ₂ + … + C_nx_n +0 × x_n ₊₁ + … + 0 × x_n ₊ _k® max. (2.7)

Т. е., мы перешли к основной задаче линейного программирования путем увеличения числа переменных на k.

Возможен и обратный переход: от ОЗЛП к задаче с ограничениями-неравен-ствами. В этом случае число переменных уменьшается.

Таким образом, всякая задача линейного программирования может быть сведена к стандартной форме ОЗЛП.

Существование решения ОЗЛП

Рассмотрим основную задачу линейного программирования с системой ограничений вида (2.2) и целевой функций (2.3).

Назовем допустимым решением любую совокупность переменных x₁ ³ 0, ..., x_n ³ 0 , удовлетворяющую системе ограничений.

Оптимальным назовем то из допустимых решений, которое обращает в максимум функцию L (2.3).

ОЗЛП не обязательно имеет решение. Это возможно в следующих случаях:

1. Уравнения в системе ограничений могут быть несовместны (противоречат друг другу).

2. Уравнения совместны, но не в области неотрицательных решений.

И в том и в другом случае задача не имеет допустимого решения.

3. Допустимые решения ОЗЛП существуют, но среди них нет оптимального: функция L в области допустимых решений не ограничена сверху.

В этом случае задача не имеет оптимального решения.

Рассмотрим вопрос о существовании допустимого решения.

При этом функцию L можно из рассмотрения исключить, так как она не влияет на существование допустимое решение.

Существуют ли значения переменных x₁,x₂,...,x_n удовлетворяющие системе уравнений (2.2).

Этот вопрос рассмотрен в линейной алгебре.

Матрицей системы линейных уравнений называется таблица, составленная из коэффициентов при переменных x₁,...,x_n.

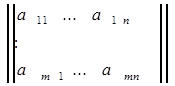. (2.8)

Расширенная матрица – это матрица, дополненная столбцом свободных членов.

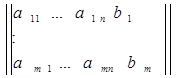. (2.9)

Рангом матрицы называется наибольший порядок отличного от нуля определителя, который можно получить из матрицы, вычеркивая какие-то строки и какие-то столбцы.

Для совместимости системы необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.

Общий ранг r – ранг совместной матрицы, называется рангом системы. Он представляет собой число линейно независимых уравнений среди наложенных ограничений.

Очевидно, что

r £ m , (2.10’)

r £ n. (2.10”)

Структура задач линейного программирования существенно зависит от ранга системы.

Если число уравнений системы равно числу переменных, т. е. n = m, то

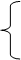a₁₁x₁+a₁₂x₂+ … +a_1nx_n=b₁,

: (2.11)

a_n1x₁+a_n2x₂+ … + a_nnx_n = bn .

Тогда все уравнения линейно независимы, то есть ранг системы равен числу переменных r = n.

Поэтому можно вычислить определитель этой системы D _n ¹ 0 и определить решение.

Если среди элементов найденного решения есть хотя бы одно отрицательное значение, то данное решение недопустимо. Если все элементы решения неотрицательны, то найденное решение является допустимым и оно же является оптимальным, так как оно единственное.

Этот тривиальный случай рассматривать не будем.

Если число уравнений системы меньше числа переменных m < n , и если система уравнений совместна, то у нее существует бесчисленное множество решений. При этом n – r переменным мы можем придавать произвольные значения, назовем эти переменные свободными; а остальные r переменных будут выражаться через эти свободные, и эти r переменных назовем базисными переменными.

Пример.

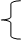2 x ₁ - x ₂ + x ₃ – x ₄ =1,

– x ₁ + x ₂ – 2 x ₃ + x ₄ =2.

Ранг системы r = 2; x ₃ и x ₄ – свободные переменные; x ₁ и x₂ – базисные переменные.

Выразим x ₁ и x ₂ через x ₃ и x ₄ и получим

x ₁ = 3 + x ₃ ,

x ₂ = 5 – x ₃ + 3 x ₃ .

Придавая различные значения переменным x ₃ и x ₄, получим значения переменных x ₁ и x ₂. Таким образом, найдем совокупность решений, которые будут удовлетворять системе уравнений ограничений.

Среди этих допустимых решений надо определить оптимальное решение.

Для этого удобно использовать геометрическую интерпретацию задачи линейного программирования.

2.3. Геометрическая интерпретация ОЗЛП

Чтобы представить себе принципиальную сторону ОЗЛП, обратимся к геометрической интерпретации. Пусть число уравнений m на два меньше числа переменных n (n – m = k = 2). Тогда 2 переменные можно выбрать в качестве свободных. Такой частный случай дает возможность геометрической интерпретации ОЗЛП на плоскости.

Мы знаем, что m линейно независимых уравнений всегда можно разрешить относительно каких-то базисных переменных, выразив их через остальные, свободные, число которых равно n – m = k (в нашем случае k = 2). Для простоты положим, что свободные переменные – это x₁ и x₂, а остальные: x₃, x₄, ... , x_n – базисные. Тогда система уравнений примет следующий вид:

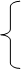x ₃ = a ₃₁ x ₁ + a ₃₂ x ₂ + b ₃ ,

× × × × × × × × × (2.12)

x_n = a _n ₁ x ₁ + a _n ₂ x ₂ + b _n .

Дадим задаче линейного программирования геометрическую интерпретацию. По осям 0 x ₁ и 0 x ₂ будем откладывать значения свободных переменных x ₁ и x ₂.

Построим на плоскости x₁0x₂ область допустимых решений или же убедимся, что ее не существует. Так как значения переменных x ₁ и x ₂ неотрицательны, то допустимые значения свободных переменных лежат в 1-ом квадранте. Базисные переменные x₃, x₄, ..., x_n тоже должны быть неотрицательными и удовлетворять уравнениям (2.12). Каждое такое уравнение ограничивает область допустимых решений. Действительно, положим в первом уравнении (2.12) x₃ = 0; получим уравнение прямой линии:

a ₃₁ x₁+ a ₃₂ x₂+ b ₃ = 0. (2.13)

На этой прямой x₃= 0; по одну сторону от нее x₃> 0, по другую – x₃ < 0.

Отметим штриховкой ту сторону (полуплоскость), где x₃ > 0 (рис. 1). Пусть эта сторона оказалась левее и ниже прямой x₃= 0. Значит, вся область допустимых решений лежит в первом координатном угле, левее и ниже прямой x₃ = 0. Аналогично поступим и со всеми остальными условиями (2.12). Каждое из них изобразится прямой со штриховкой, указывающей "допустимую" полуплоскость, где только и может лежать решение (рис. 1).

Таким образом, мы построили n прямых: две оси координат и n – 2 прямых x₃= 0, x₄ = 0, ..., x_n = 0. Каждая из них определяет "допустимую" полуплоскость, где может лежать решение.

x ₂

x ₃ =0

x ₄ =0

x ₅ =0

ОДР

0 x ₁

Рис. 1.

Часть первого координатного угла, принадлежащая одновременно всем этим полуплоскостям, и есть область допустимых решений (ОДР). На рис. 1 показан случай, когда ОДР существует, т. е. система уравнений (2.12) имеет неотрицательные решения. Заметим, что этих решений – бесконечное множество, так как любая пара значений свободных переменных, взятая из ОДР, удовлетворяет системе уравнений, а из x₁ и x₂ могут быть определены и базисные переменные.

Опорными точками будем называть вершины ОДР.

Может оказаться, что ОДР не существует, и значит, уравнения (2.12) несовместны в области неотрицательных значений.

ОДР всегда представляет собой выпуклый многоугольник.

После построения ОДР в этой области нужно найти оптимальное решение.

Для этого дадим геометрическую интерпретацию условию (2.3), т. е.

L = c₁x₁+c₂x₂+...+c_nx_n ® max. (2.14)

Подставив уравнения (2.12) в формулу (2.3), выразим L через свободные переменные x₁, x₂. После приведения подобных членов получим:

L = g ₁ x₁+ g ₂ x₂+ g ₀ , (2.15)

где g ₁ , g ₂ – какие-то коэффициенты, g ₀ – свободный член, которого в первоначальном виде у функции L не было; теперь, при переходе к переменным x₁, x₂

он мог и появиться. Однако максимум линейной функции L достигается при тех же значениях x₁, x₂, что и максимум однородной линейной функции (без свободного члена):

L' = g ₁ x₁ + g ₂ x₂, (2.16)

поэтому свободный член g ₀ отбрасываем.

Посмотрим, как изобразить геометрически условие L' ® max. Положим сначала L' = 0, т.е. g ₁ x₁ + g ₂ x₂ = 0 и построим на плоскости прямую с таким уравнением; очевидно, она проходит через начало координат. Назовем ее "опорной прямой".

Отмечаем на рисунке стрелками, поставленными у опорной прямой, то направление, в котором L' возрастает. Направление зависит от коэффициентов g ₁, g ₂. Теперь изображаем опорную прямую и ОДР на одном чертеже. Мысленно будем двигать опорную прямую параллельно самой себе в направлении стрелок (возрастания L').

Когда L' достигнет максимума? Очевидно, в точке A – крайней точке ОДР в направлении стрелок (рис. 2). В этой точке свободные переменные принимают оптимальные значения x₁*, x₂*. Зная их, можно найти и оптимальные значения всех остальных (базисных) переменных x₃*, x₄*, ..., x_n*. Заметим, что максимум L' достигается в одной из вершин ОДР, где, по крайней мере, две из базисных переменных обращаются в нуль. Если бы через точку A проходило более двух прямых x_i = 0, то в нуль обращалось бы большее число базисных переменных.

x₂

x₃=0 x₄=0

x₅=0

ОДР A

0 x₁

L’=0

Рис. 2.

Если число независимых уравнений, которым должны удовлетворять переменные на два меньше, чем число самих переменных n – m = 2, то решение основной задачи линейного программирования может быть получено простым геометрическим построением.

Несмотря на то, что такое построение относится к частному случаю, из него можно сделать выводы, относящиеся вообще к свойствам решения ОЗЛП.

Свойства решения:

1. Решение ОЗЛП, если оно существует, не может лежать внутри области допустимых решений, а только на ее границе.

2. Решение ОЗЛП может быть и не единственным, если опорная прямая L' параллельна той стороне многоугольника допустимых решений, где достигается максимум. В этом случае задача имеет бесчисленное множество решений.

3. ОЗЛП может не иметь решения даже в случае, если существует ОДР. Это возможно, когда в направлении возрастания целевой функции ОДР не ограничена (рис. 3).

4. Решение ОЗЛП, максимизирующее функцию L', то есть оптимальное решение, всегда достигается в одной из вершин многоугольника допустимых решений.

x ₂

ОДР

0 x ₁

Рис. 3.

5. Для того, чтобы найти оптимальное решение достаточно перебрать все опорные точки и выбрать из них ту, для которой функция L максимальна.

6. Если число свободных переменных в ОЗЛП равно двум, число базисных переменных m и решение ОЗЛП существует, то оно всегда достигается в точке, где, по крайней мере, две из переменных обращаются в ноль. Возможен случай, когда через опорную точку проходит большее число прямых. Такой случай называется вырожденным (рис. 4).

Если число свободных переменных равно 3 (n – m = 3), то геометрическая интерпретация имеет место в пространстве. При этом x ₁ , x ₂ , x ₃ – свободные переменные, а уравнение x_k = 0 – уравнение плоскости:

x_k = a _k1 x₁ + a _k2 x₂ + a _k3 x₃ + b _k = 0. (2.17)

x₂

x ₃ =0

x ₄ =0

x ₅ =0

x ₆ =0

ОДР

0 x ₁

Рис. 4.

ОДР, если она существует, будет представлять собой выпуклый многогранник. Роль опорной прямой у основания плоскости:

L ^* = g ₁ x ₁ + g ₂ x ₂ + g ₃ x ₃ . (2.18)

При перемещении этой плоскости параллельно самой себе в одну сторону L ’ будет возрастать, в другую убывать. Точка А, в которой достигается оптимальное решение, если оно существует, будет представлять собой ту вершину ОДР, которая наиболее удалена от начала координат в направлении возрастания L ’.

Задача имеет бесчисленное множество решений, если основная плоскость пересекает ребро этого многогранника, либо пересекает грань.

Возможен случай, когда задача не имеет решения, ОДР не ограничена.

В опорной точке по крайней мере 3 из n переменных обращаются в ноль.

Геометрическая интерпретация, как таковая, теряет свою наглядность, однако можем использовать терминологию, т.е. говорить об ОДР, как о некотором гипермногограннике, ограниченном гиперплоскостями.

Укажем свойства решения ОЗЛП для любого числа переменных и уравнений.

1. Оптимальное решение, если оно существует, лежит не внутри, а на границе области допустимых решений в одной из опорных точек, в каждой из которых по крайней мере k (где k = n – m) переменных, обращается в ноль.

2. Чтобы найти оптимальное решение, нужно переходя от одной опорной точки к другой, двигаться в направлении возрастания линейной функции L, которую необходимо максимизировать.

2.4. Симплекс-метод решения ОЗЛП

2.4.1. Суть симплекс-метода

Суть симплекс-метода вытекает из свойств решения ОЗЛП.

Пусть имеется произвольная задача линейного программирования, с числом переменных n и числом уравнений m. Оптимальное решение, если оно существует, достигается в одной из опорных точек, в которой, по крайней мере, k из n переменных обращаются в нуль:

k = n – m. (2.19)

Выберем в качестве свободных эти k переменных, остальные m будут базисными. Для определенности в качестве свободных выберем первые k переменных: x ₁ , ¼ , x _k. Остальные x _{k+1 ,} ¼ , x _n базисные переменные можно выразить через эти свободные.

Целевая функция, выраженная через свободные переменные, имеет вид

L = g ₀ + g ₁ x₁+...+ g _k x_k ® max. (2.20)

Оптимальное решение всегда лежит в одной из опорных точек, в которой по крайней мере k переменных обращается в ноль. Положим эти k переменных равными нулю, получим опорное решение

x ₁ = x ₂ = ... = x _k = 0. (2.21)

Предположим, что все коэффициенты в целевой функции при переменных x₁, x₂, ¼, x_k отрицательны, тогда

L = g₀ , (2.22)

и найденное опорное решение является оптимальным.

Если коэффициент при какой-то переменной x _i в целевой функции больше нуля, то имеет смысл увеличивать переменную x _i. Это означает, что переменную x _iнужно вывести из разряда свободных и перевести ее в разряд базисных, а взамен ей ввести другую переменную. Увеличивать x _i до бесконечности нельзя, так как имеется система уравнений-ограничений.

Если для какой-то переменной x_r

x_r = a_r1x₁+...+a_rix_i+...+a_rkx_k+b_r (2.23)

коэффициент при свободной переменной x_i меньше нуля, то увеличивать переменную x_i можно только до тех пор, пока переменная x_r не станет равной нулю

x_i ^r = – b_r / a_ri . (2.24)

Предположим, что есть еще одна переменная x_l

x_l = a_l1x₁+...+a_lix_i+...+a_lkx_k+b_l , (2.25)

для которой коэффициент при x_i тоже меньше нуля. Тогда предел увеличения переменной x_i для этой переменной

x_i ^l = – b_l / a_li . (2.26)

Очевидно, что увеличивать переменную x _i можно до того значения, которое является минимальным, то есть для той из переменных, которая быстрее обращается в нуль. Предположим, что в ноль быстрее обращается переменная x _r . Тогда эти две переменные мы должны поменять местами, то есть i-ую переменную из свободных перевести в базисные, а r-ую – из базисных в свободные. Необходимо

переразрешить систему ограничений и саму целевую функцию относительно нового набора базисных и свободных переменных:

x ₁ , x ₂ , ... , x_i _–1 , x_i ₊₁ , ..., x_k , x_r – свободные переменные,

x_i , x_k ₊₁ , ..., x_r _–1 , x_r ₊₁ , ..., x_n – базисные переменные.

Тем самым мы перешли в другую опорную точку. Далее вся процедура повторяется.

Заметим, что если какие-то из свободных членов в системе ограничений отрицательны, то необходимо осуществить аналогичным образом замены переменных, то есть переразрешать уравнения до тех пор, пока все свободные члены не станут неотрицательными.

2.4.2. Табличный алгоритм замены базисных переменных

Процедура переразрешения системы уравнений и целевой функции относительно новых базисных переменных может быть существенно упрощена, если ее формализовать и свести к заполнению стандартной таблицы по определенному алгоритму.

Обозначим через x_i свободные переменные, через y_j – базисные переменные.

Пусть есть система ограничений:

Предположим, что мы решили поменять местами базисную переменную y₃ и свободную переменную x₂, для этого необходимо выразить x₂ из третьего уравнения (a ₃₂ ¹ 0) и подставить во все остальные.

y₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + a₁₄x₄ + b₁ ,

y₂ = a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + a₂₄x₄ + b₂ ,

y₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + a₃₄x₄ + b₃ , (2.27)

y₄ = a₄₁x₁ + a₄₂x₂ + a₄₃x₃ + a₄₄x₄ + b₄ ,

y₅ = a₅₁x₁ + a₅₂x₂ + a₅₃x₃ + a₅₄x₄ + b₅ .

Чтобы не переписывать много раз систему уравнений, вместо них используют таблицу (табл. 2), в которую заносят свободные члены и коэффициенты при свободных переменных.

Чтобы заполнить таблицу, необходимо систему уравнений привести к стандартному виду, то есть представить каждое уравнение в виде разности между свободным членом и суммой всех остальных членов, например

y₁ = b₁ – (– a₁₁x₁ – a₁₂x₂ – ... – a₁₄x₄). (2.28)

В таблице выделяют столбец и строку, где находятся базисная и свободная переменные, которые мы хотим поменять местами. Строка и столбец, в которых они находятся, называются разрешающей строкой и разрешающим столбцом. На их пересечении находится разрешающий элемент.

Таблица 2

	b_i	x₁	x₂	x₃	x₄
y₁	b ₁	-a ₁ ₁	-a ₁ ₂	-a ₁ ₃	-a ₁ ₄
y₂	b ₂	-a ₂ ₁	-a ₂ ₂	-a ₂ ₃	-a ₂ ₄
y₃	b ₃	-a ₃ ₁	-a ₃ ₂	-a ₃ ₃	-a ₃ ₄
y₄	b₄	-a₄₁	-a₄ ₂	-a ₄ ₃	-a₄₄
y₅	b₅	-a₅₁	-a₅₂	-a₅₃	-a ₅ ₄

Алгоритм замены следующий:

1) разрешающий элемент заменяется на обратную ему величину;

2) все элементы разрешающей строки делятся на разрешающий элемент;

3) все элементы разрешающего столбца, кроме разрешающего элемента, меняют знак на противоположный и делятся на разрешающий элемент;

4) каждый из остальных элементов подвергается следующему преобразованию: к нему прибавляется произведение элемента, стоявшего в прежней разрешающей строке на том же месте по порядку, то есть в том же столбце, на элемент, стоящий в новом разрешающем столбце на соответствующем месте, то есть в той же строке.

Эти правила справедливы для любого числа свободных и базисных переменных и для любых замен.

Для удобства все вычисления производят в таблице, выделяя нижнюю часть каждой ячейки.

Алгоритм преобразования коэффициентов стандартной таблицы следующий:

1) выделить в таблице разрешающий элемент a _lk;

2) найти обратную ему величину l = 1/ a _lk и записать ее в правом нижнем углу этой же ячейки;

3) все элементы разрешающей строки, кроме разрешающего элемента, умножить на l, и результат записать в правой нижней части каждой ячейки;

4) все элементы разрешающего столбца, кроме разрешающего элемента, умножить на (– l ) и результат записать в правой нижней части ячейки;

5) подчеркнуть или выделить каким-либо иным способом в разрешающей строке все верхние числа, а в разрешающем столбце – все нижние числа;

6) для каждого из элементов, которые не принадлежат ни разрешающему столбцу, ни разрешающей строке, записать в нижнюю часть ячейки произведение выделенных чисел, стоящих в той же строке и том же столбце, что и данный элемент;

7) переписать таблицу, заменив переменные; элементы разрешающего столбца и строки – числами, стоящими в нижних частях этих ячеек; каждый из оставшихся элементов – суммой чисел, стоящих в верхней и нижней частях этой ячейки.

С помощью табличного алгоритма можно решить любую задачу линейного программирования или убедиться, что она не имеет решения. При этом решение любой задачи линейного программирования состоит из двух этапов:

1) нахождение опорного решения;

2) нахождение оптимального решения.

В процессе первого этапа выясняется имеет ли данная задача допустимое решение. Если да, то находится опорное решение.

В процессе второго этапа выясняется ограничена ли сверху целевая функция L. Если нет, то оптимального решения нет.

2.4.3. Нахождение опорного решения

Предположим, имеется система уравнений, записанная в стандартном виде

y₁ = b₁ – (a₁₁x₁ + ... + a_1nx_n),

... (2.29)

y_m = b_m – (a_m1x₁ + ... + a_mnx_n),

где y₁, ..., y_m – базисные переменные, x₁, ..., x_n – свободные переменные.

Если все свободные члены неотрицательны, то найденное решение является допустимым (b _i > 0, i =1... n). Если хотя бы один из свободных членов отрицателен, то необходимо найти опорное решение: для этого шаг за шагом будем менять местами базисные и свободные переменные до тех пор, пока не найдем опорного решения или пока не убедимся, что оно не существует.

Очевидно, что такие замены надо производить таким образом, чтобы каждый последующий шаг приближал нас к ОДР, то есть число отрицательных свободных членов должно уменьшаться, либо отрицательный свободный член – становится меньше по абсолютному значению.

Существует ряд способов выбора разрешающего элемента. Рассмотрим один из методов (без доказательства).

Пусть в системе имеется одно из уравнений с отрицательным свободным членом. В этой строчке ищем отрицательный элемент a_ij. Если такого элемента нет, следовательно, система уравнений несовместна.

Если есть отрицательный элемент a_ij, то столбец, в котором он стоит, выбирается в качестве разрешающего.

Далее в этом столбце нужно выбрать разрешающий элемент. Для этого рассматриваются все элементы этого столбца, имеющие одинаковый знак со своим свободным членом. Из этих элементов в качестве разрешающего выбирается тот, отношение к которому свободного члена минимально.

2.4.4. Определение оптимального решения

Сформулируем правило нахождения оптимального решения.

1. Если все свободные члены, не считая строки L, в симплекс-таблице неотрицательны, а в строке L, не считая свободного члена, нет ни одного отрицательного элемента, значит, оптимальное решение достигнуто.

2. Если в строке L, не считая свободного члена, есть отрицательный элемент, а в столбце, соответствующем ему, нет ни одного положительного элемента, значит, целевая функция не ограничена сверху и оптимального решения не существует.

3. Если в строке L есть отрицательный элемент и в столбце, соответствующем ему есть положительный элемент, то следует произвести замену одной из свободных переменных на одну из базисных, причем в качестве разрешающего надо взять тот элемент этого столбца, для которого отношение к нему свободного члена минимально.

Дата добавления: 2019-02-12; просмотров: 608; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!