Закон парности касательных напряжений

 

В окрестностях произвольной точки напряжённого тела выделим элементарный объём в форме прямоугольного параллелепипеда со сторонами dx, dy, dz. На каждой из граней действует по три составляющих напряжения – нормальное напряжение и два касательных (рис. 20).

 

 

 

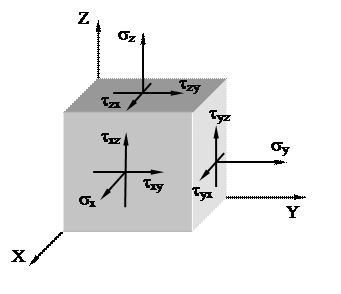Рис. 20

 

Составим уравнение равновесия выделенного элемента в форме суммы моментов всех сил относительно оси X:

 

SМ_х = 0,

s_у×dx×dz×dy - s_у×dx×dz×dy + s_z×dx×dy×dz - s_z×dx×dy×dz + t_xy×dy×dz× 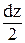 - t_xy×dy×dz×  +

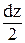+ t_xz×dy×dz× 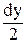 - t_xz×dy×dz×  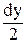+ t_zy×dx×dy×dz - t_yz×dx×dz×dy = 0,

 

приведя подобные слагаемые и упростив выражение, получим:

 

                                                          t_zy = t_yz.                                                   (29)

 

Составляя уравнения равновесия относительно осей Y и Z, получим аналогичные выражения:

 

                                                          t_zх = t_хz,                                                   (30)

t_хy = t_yх.

 

Полученные выражения (29), (30) определяют закон парности касательных напряжений: касательные напряжения на взаимно перпендикулярных площадках равны по величине и направлены либо к общему ребру, либо от него.

 

Напряжения на наклонных площадках

 

Элементарный объём в форме параллелепипеда, расположенный таким образом, чтобы его грани совпадали с координатными плоскостями, рассечем наклонной плоскостью (рис. 21).

 

 

 

Рис. 21

 

Положение наклонной площадки характеризуется вектором нормали n с направляющими косинусами l, m, n. На наклонной площадке площадью dF действует полное напряжение Р с проекциями по осям Р_х, Р_у, Р_z. Пусть нормальные и касательные напряжения на гранях, совпадающих с координатными плоскостями, известны. Необходимо найти нормальное и касательное напряжение на наклонной площадке – s_n и t_n. Площадки, отсекаемые на координатных плоскостях, будут иметь площади:

 

dF_x = dF×l, dF_y = dF×m, dF_z = dF×n.

 

Составим уравнение равновесия сил в проекции на ось Х:

SХ = 0,

P_x×dF - s_x×dF_x - t_yx×dF_y - t_zx×dF_z = 0,

P_x×dF - s_x×dF×l - t_yx×dF×m - t_zx×dF×n = 0,

                                           P_x = s_x×l + t_yx×m + t_zx×n.                                          (31)

 

Аналогично, составляя уравнения равновесия сил на оси Y и Z, получаем выражения для двух других проекций полного напряжения:

 

P_y = t_xy×l +s_y×m + t_zy×n,

                                               P_z = t_xz×l + t_yz×m +s_z×n.                                       (32)

 

Чтобы определить нормальное напряжение на наклонной площадке, спроецируем проекции полного напряжения на нормаль.

 

s_n = P_x×l + P_y×m + P_z×n =

= s_x×l² + t_yx×m×l + t_zx×n×l + t_xy×l×m +s_y×m² + t_zy×n×m + t_xz×l×n + t_yz×m×n +s_z×n² .

С учетом закона парности касательных напряжений – (29) и (30),  получаем основную квадратичную форму нормальных напряжений:

 

                     s_n = s_x×l² + s_y×m² +s_z×n² + 2t_yx×m×l + 2t_zx×n×l + 2t_zy×n×m.                  (33)

 

Полученное выражение позволяет определить нормальное напряжение на любой наклонной площадке, поскольку при выводе этого выражения никаких ограничений на положение площадки не накладывалось. Теперь найдем величину касательного напряжения на наклонной площадке:

 

Р² = P_x² + P_у²+ P_z² = s_n² + t_n²,

                                             t_n²= P_x² + P_у²+ P_z² - s_n².                                        (34)

---

Дата добавления: 2018-11-24; просмотров: 374; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!