Деление отрезка в данном отношении
Пусть дан отрезок АВ и некоторое число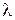 
, требуется найти на отрезке точку С так, чтобы 
.
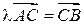Рассмотрим радиус-векторы точек А и В – а и b, обозначим радиус–вектор неизвестной точки С – х.
Тогда
Отсюда следует, что
или
Таким образом,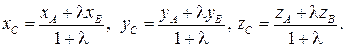 
Замечания:
1) если точка С – середина отрезка, тогда 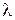=1;
2) если точка С делит отрезок в отношении 1:2, тогда 
=2;
3) формула остается верной и при 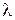=0, так как в этом случае точка С совпадает с точкой В.
Скалярное произведение векторов
Определение 2.5.1. Скалярным произведением двух векторов 
называется число, обозначаемое символам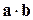и 
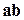или 
, или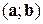 
, равное произведению длин этих векторов на косинус угла между ними:
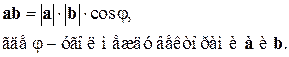
Из определения очевидно, что для нахождения угла между векторами можно использовать следующую формулу:
.
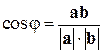Свойства скалярного произведения:
1) скалярный квадрат вектора равен квадрату его длины
;
2) коммутативность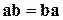 
;
3) 
;
4) дистрибутивность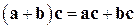 
;
5) если для любого ненулевого вектора d 
, тогда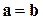 
;
6) условие ортогональности векторов:
Ненулевые векторы ортогональны тогда и только тогда, когда их скалярное произведение равно нулю
.
7) 
;
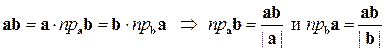8) скалярное произведение не ассоциативно 
.
Скалярное произведение в координатах.
Пусть а, b – произвольные векторы с координатам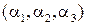и 
и 
, соответственно. Тогда скалярное произведение этих векторов определяется формулой:
.
Используя первое свойство скалярного произведения, получаем
|
|
|
.
Пример 2.5.1.
Даны вершины треугольника: А(2;–1;3), В(1;1;1), С(0;0;5). Найдите длину стороны АВ и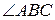 
.
Решение.
, 
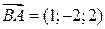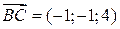, АВ= 
.
.
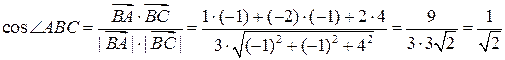Значит,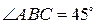 
.
Пример 2.5.2.
Определить длины диагоналей параллелограмма, построенного на векторах 
и 
, где m и n – единичные векторы, угол между которыми равен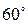 
.
Решение.
В этой задаче не заданы координаты векторов в ортонормированном базисе 
. Поэтому воспользоваться формулами скалярного произведения так просто не получится.
Сделав схематический рисунок (рис. 2.14),
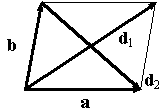
Рис.2.14. Диагонали параллелограмма
убеждаемся, что вектор d1, соответствующий одной диагонали параллелограмма, находится по формуле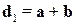 
, а другой – 
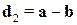. Отсюда 
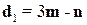и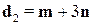 
. В силу первого свойства скалярного произведения получим
Аналогично,
Векторное произведение векторов
Определение 2.6.1. Тройка векторов называется правой (левой), если, наблюдая с конца третьего вектора, движение первого вектора ко второму по меньшему из углов происходит против (по) часовой стрелки (рис. 2.15).
левая правая
Рис.2.15. Тройки векторов
Определение 2.6.2. Векторное произведение двух векторов 
есть новый вектор с, определяемый условиями:
|
|
|
1) 
, 
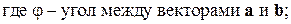
2) 
и 
;
3) тройка векторов 
– правая.
Свойства векторного произведения:
1) 
равна площади параллелограмма, построенного на 
, 
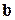как на сторонах (рис. 2.16).
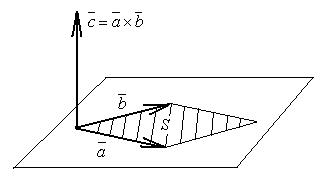
Рис.2.16. Площадь параллелограмма
Следствие. Площадь треугольника, построенного на векторах , ,
.
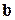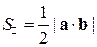2) векторное произведение антикоммутативно
;
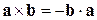3) 
;
4) дистрибутивность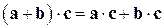 
.
5) соблюдено условие коллинеарности векторов.
Ненулевые вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору
.
Следствие 
.
Векторное произведение в координатах
Пусть а, b – произвольные вектора с координатам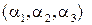и 
и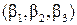 
. Тогда
Следствие. Ненулевые векторы коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Пример 2.6.1.
Пусть вершины треугольника расположены в точках А(1,–1,2), В(2,2,1), С(0,4,–1). Найдите площадь треугольника.
Решение.
По следствию из 1 свойства векторного произведения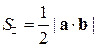 
. Находим 
,
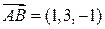То есть 
Тогда 
.
Дата добавления: 2018-11-24; просмотров: 189; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!