Система координат. Координаты вектора

Векторная алгебра

Векторы

Определение 2.1. Вектором называется упорядоченная пара точек пространства. Первая точка – начало вектора, вторая – его конец, который на рисунке обозначается стрелкой.

В математической литературе векторы обозначаются обычно одним из следующих способов: . В двух последних случаях А – обозначение точки, являющейся началом вектора, В – концом вектора. В тексте этого пособия будут использоваться первое и последнее из перечисленных обозначений (рис. 3.1).

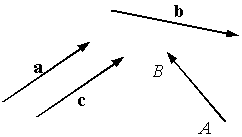
Рис. 2.1. Изображение векторов

Определение 2.2. Вектора называются коллинеарными а||b, если они лежат на одной прямой или на параллельных прямых.

Определение 2.3. Вектора называются прямоколлинеарными 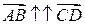, если точки A и C лежат по одну сторону от прямой, проходящей через B и D .

Определение 2.4. Вектора называются противоколлинеарными 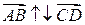, если точки A и C лежат по разные стороны от прямой, проходящей через B и D .

Определение 2.5. Длина вектора – длина отрезка, определяющего вектор.

Обозначается длина . Вектор а называется единичным, если .

Определение 2.6. Два вектора называются равными, если они прямоколлинеарны и имеют одинаковую длину.

Если считать, что на рисунке векторы лежат в одной плоскости, то а = с, то есть а ис – разные обозначения одного и того же вектора. Векторы а и при равных длинах не равны друг другу, так как имеют разные направления. В соответствии с введенным равенством векторов слова "вектор параллелен прямой (плоскости)" и "вектор лежит на прямой (плоскости)" означают одно и то же, так как направленный отрезок можно передвинуть параллельно самому себе, вектор при этом не изменится.

Определение 2.6 . Векторы называются компланарными, если они параллельны одной плоскости (рис. 2.2).

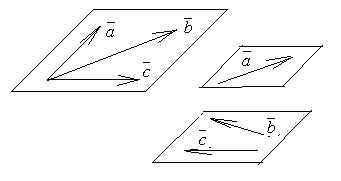
Рис. 2.2. Компланарные векторы

К множеству векторов необходимо добавить еще один объект, который мы будем называть нулевым вектором. Его можно рассматривать как отрезок, у которого начало и конец совпадают. Длина такого вектора равна нулю, направления он не имеет. Все нулевые векторы равны друг другу. Так как нулевой вектор лежит на любой прямой, то, по определению, он считается коллинеарным любому вектору и перпендикулярным любому вектору.

В соответствии с принятыми выше обозначениями следовало бы нулевой вектор обозначать 0, но принято обозначать 0. По контексту всегда ясно, чем является 0, числом или вектором.

Операции с векторами

Сложение векторов

Определение. Пусть даны векторы a и b, тогда их сумма - вектор с, который идет из начала вектора a в конец вектора b , если вектор b приложен к концу вектора a (показан на рис. 2.3.)

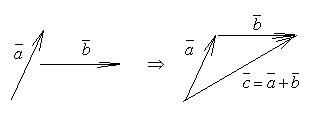
Рис.2.3. Сложение векторов по правилу треугольника.

Свойства операции сложения:

1) коммутативность a + b = b + a;

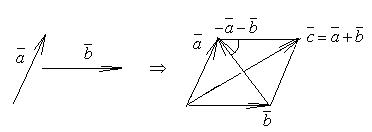
Рис. 2.4. Правило параллелограмма

2) ассоциативность (a + b) + с = a +(b + с);

Из свойства ассоциативности следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить. Как найти сумму нескольких слагаемых, не используя попарных сумм, видно из рисунка 2.5.

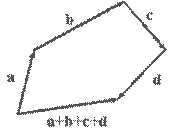
Рис.2.5. Сложение трёх и более векторов

3)a + 0 = a;

4) для любого вектора a существует противоположный вектор (–a ), что a + (–а) = 0.

Умножение вектора на число (рис. 3.6).

Определение. Вектор с – произведение вектора а на число 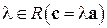, если 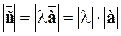и вектор спрямоколлинеарен а, если 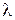> 0, вектор спротивоколлинеарен а, если l < 0.

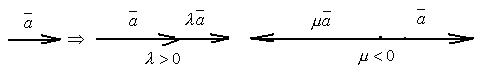
Рис.2.6. Умножение вектора на число

Свойства умножения на число:

5) ;

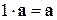6) ассоциативность по умножению чисел

, ;

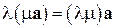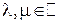7)дистрибутивность по сложению чисел

, ;

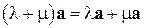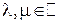8) дистрибутивность по сложению векторов

, ;

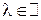9) для любых векторов a и b существует такой вектор x, что 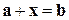(x называется разностью векторов a и b);

10) .

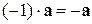Проекции вектора.

Пусть в пространстве задана некоторая ось l, то есть прямая, на которой отмечена фиксированная точка О и заданы направление и единица длины. Тогда каждой точке оси соответствует некоторое число. А также задана произвольная прямая 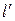или плоскость .

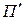Определение. Проекцией произвольного вектора на ось l параллельно прямой 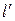называется число, соответствующее длине отрезка, полученного при пересечении с осью l прямыми, проходящими через А и В параллельно прямой 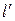(рис. 2.7).

Рис. 2.7. Проекция вектора на ось параллельно прямой

Определение. Проекцией произвольного вектора на плоскость П параллельно плоскости 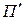называется число, соответствующее длине отрезка, полученного при пересечении с плоскостью П плоскостями, проходящими через А и В параллельно плоскости 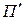. Величина проекции определяется аналогично (рис. 2.8.).

Рис.2.8. Проекция вектора на ось параллельно плоскости

На практике чаще используют так называемую ортогональную проекцию, опуская на ось перпендикуляры.

Утверждение 2.2.1. Пусть 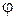– угол, образованный вектором a с осью l . Тогда ортогонольная проекция вектора a на осьl равна произведению длины этого вектора на косинус угла между вектором и осью: .

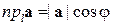Утверждение 2.2.2. Проекция на ось суммы векторов равна сумме их проекций.

Утверждение 2.2.3.Проекция на ось вектора, умноженного на число, равна произведению проекции вектора на это число.

Определение 2.2.3.Проекцией вектора b на вектор a, 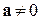, будем называть проекцию вектора b на любую ось, параллельную вектору a и имеющую направление, совпадающее с направлением вектора a.

Проекция вектора b на вектор a обозначается .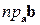

Очевидно, что 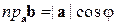, где 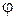– угол между векторами a и b (рис. 2.9).

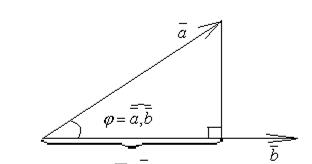
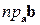
Рис.2.9. Проекция вектора на вектор

Система координат. Координаты вектора

Определение 2.3.1. Базисом векторного пространства V будем называть упорядоченную систему векторов пространства, состоящую из одного ненулевого вектора, если пространство одномерное; из двух неколлинеарных векторов, если пространство двумерное; из трех некомпланарных векторов, если пространство трехмерное.

Определение 2.3.2. Базис называется ортогональным, если векторы взаимно перпендикулярны.

Определение 2.3.3. Базис называется нормированным, если все его векторы имеют единичную длину.

Определение 2.3.4. Базис называется ортонормированным, если он является и ортогональным, и нормированным.

Пример 2.3.1. Ортонормированный базис пространства 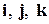(рис. 2.10).

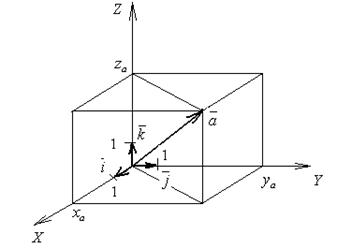
Рис. 2.10. Ортонормированный базис пространства

Пример 2.3.2. Ортонормированный базис плоскости (рис.2.11).

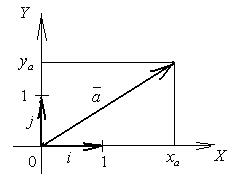
Рис. 2.11. Ортонормированный базис плоскости

Определение 2.3.5. Система координат – это базис и заданное начало отсчёта О (произвольная точка).

Определение 2.3.6. Пусть задана система координат Оxyzи произвольный вектор , тогда координаты этого вектора –

– проекция на ось х параллельно плоскости Оyz – ;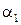

– проекция на ось у параллельно плоскости Оxz – ;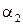

– проекция на ось z параллельно плоскости Оxy – ;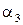

Тогда в соответствии с определением базиса

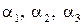Замечание. Для указания, что вектор имеет координаты мы будем использовать запись .

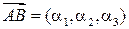Определение 2.3.7. Косинусы углов, образованных вектором с осями координат, называются направляющими косинусами вектора.

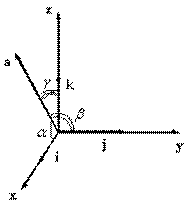
Рис. 2.12. Направляющие косинусы вектора

В соответствии с рисунком 2.12, направляющими косинусами вектора a являются .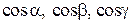

Утверждение 2.3.1. При умножении вектора на число все его координаты умножаются на это число.

Утверждение 2.3.2. При сложении векторов складываются их соответствующие координаты.

Определение 2.3.8. В системе координат Оxyz координаты радиус-вектора 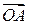некоторой точки А совпадают с координатами этой точки.

Утверждение 2.3.3. Если заданы координаты начала и конца вектора , то координаты этого вектора находятся следующим образом: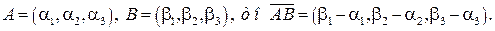

Дата добавления: 2018-11-24; просмотров: 203; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!