Уточнение решения задачи Методом золотого сечения.
Алгоритм поиска экстремума функции f(x) на интервале [a0; b0] с использованием метода золотого сечения состоит из следующих шагов :
1 Задать a0, b0 – границы интервала поиска экстремума функции f(x);
t = 0.618 - константа.
2 Вычислить
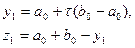и значение f(y1), f(z1).
3 Если f(y1) £ f(z1), то положить a1 = a, b1 = z1 и перейти к п. 4; иначе положить a1 = y1, b1 = b0 и перейти к п. 4.
4 Положить k = 1.
5 Если f(yk) £ f(zk), то вычислить yk+1 = ak+bk-yk, f(yk+1) и перейти к п.6; иначе положить yk+1 = zk, f(yk+1) = f(zk) и перейти к п. 7.
6 Положить zk+1 = yk, f(zk+1) = f(yk) и перейти к п. 8.
7 Вычислить zk+1 = ak+bk-zk, f(zk+1) и перейти к п. 8.
8 Если f(yk+1) £ f(zk+1), то положить ak+1 = ak, bk+1 = zk+1 и перейти к п.9; иначе положить ak+1 = yk+1, bk+1 = bk и перейти к п. 9.
9 Вычислить xk = (ak+1 + bk+1) / 2.
10 Если k = 1, то перейти к п. 5; иначе перейти к п. 11.
11 Если | xk-1 – xk | £ e, то закончить поиск, иначе положить k = k+1 и перейти к п.5
Для нахождения экстремума этим методом используем отрезок [а,b], где а и b были найдены в предыдущем разделе на последнем этапе.
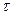- вычислим по формуле 
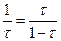, где l – длина нашего отрезка.
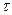- будем писать как T).
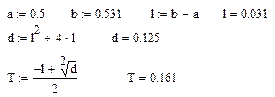
1:
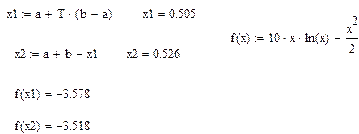
На 2-й итерации исходя из того что значение функции в точке x1 было меньше, конец отрезка b переноситься в точку x2, точка x1 остается прежней, и вычисляется новое значение точки x2.
2:
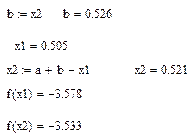
На предыдущей итерации f(x2)>f(x1), а следовательно необходимо снова перенести конец отрезка в точку x1.
3:
Аналогично проделываем еще две итерации для нахождения экстремума заданной функции.
|
|
|
4:
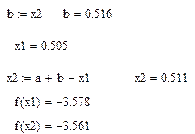
5:
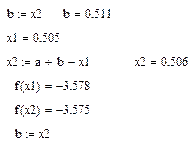
Вычисленный экстремум в точке x1 = 0.505 . Оставшийся отрезок :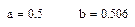 
4.4 Уточнение решения задачи методом квадратичной аппроксимации.
Описание алгоритма метода последовательного оценивания с использованием квадратичной аппроксимации :
1 Пусть f(x) – оптимизируемая функция, х1 – начальная точка, Dх – величина шага по оси абсцисс. Вычислить х2 = х1+Dх и значения функции f(x1) и f(x2).
2 Если f(x1) >f(x2), то положить х3 = х1 +2 Dх. Если f(x1) £ f(x2), то положить х3 = х1 -Dх.
3 Вычислить значение функции f(x3). Найти fmin = min{ f(x1), f(x2), f(x3)}, xmin – точка, которой соответствует fmin.
4 По трем точкам x1, x2, x3 вычислить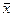 
по формуле 
.
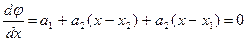5 Произвести проверку на окончание поиска минимума. Если разности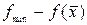 
и 
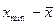являются достаточно малыми величиннами, то закончить поиск; иначе перейти к п. 6.
6 Выбрать «наилучшую» точку (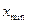 
или 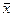) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к п. 3.
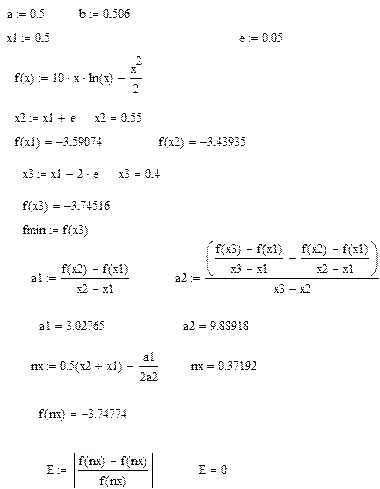
В итоге мы вычислили минимальное значение функции на заданном отрезке [0.5 ; 1], с точностью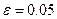 
, оно находиться в точке x1 = 0,5 ; f(x) = – 3,59074 ;
Поиск локального максимума функции
Метод нулевого порядка - метод Хука – Дживса
|
|
|
Метод Хука-Дживса был разработан в 1961 году, но до сих пор является весьма эффективным и оригинальным. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которой в случае успеха следует поиск по образцу. Он применяется для решения задачи минимизирования функции без учета ограничений.
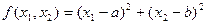a=0 b=8 X0[0;0] e=0,3 e=0,5
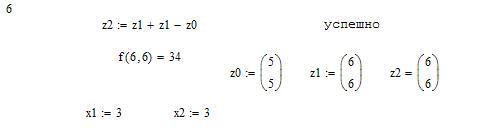
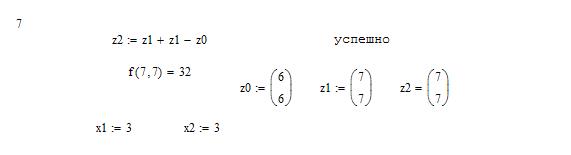
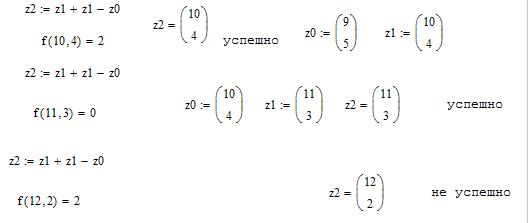
Дата добавления: 2018-10-27; просмотров: 194; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!