Целочисленное программирование. Метод ветвей и границ
Из предыдущего метода было получено:
F опт = 129/22
XT ={ 7/22, 61/22 , 0 , 0 }
Введём дополнительное ограничение на x2
x2 ≤ [61/22]
x2 ≥ [61/22] + 1
x2 ≤ 2
x2 ≥ 3
Задача 1
F = x1 + 2x2 à min
5x1 + 7x2 ≤ 21
-x1 + 3x2 ≤ 8
x2 ≥ 3
x1,x2 ≥ 0
Эта задача решения не имеет
Задача 2
F = x1 + 2x2 à min
 5x1 + 7x2 ≤ 21
5x1 + 7x2 ≤ 21
-x1 + 3x2 ≤ 8
x2 ≤ 2
x1,x2 ≥ 0
 x3 = 21 – ( 5x1 + 7x2 )
x3 = 21 – ( 5x1 + 7x2 )
x4 = 8 – ( -x1 + 3x2 )
x5 = 2 – (x2 )
-F = 0 – ( x1 + 2x2 ) à min
| β | x1 | x2 | |
| x3 | 21 -14 | 5 0 | 7 -7 |
| x4 | 8 -6 | -1 0 | 3 -3 |
x5
| 2 2 | 0 0 | 1 1 |
| -F | 0 -4 | 1 0 | 2 -2 |
 λ = 1
λ = 1
| β | x1 | x5 | |
x3
| 7 7/5 | 5 1/5 | -7 -7/5 |
| x4 | 2 7/5 | -1 1/5 | -3 -7/5 |
| x2 | 2 0 | 0 0 | 1 0 |
| -F | -4 -7/5 | 1 -1/5 | -2 7/5 |
λ = 1/5
| β | x3 | x5 | |
| x1 | 7/5 | 1/5 | -7/5 |
| x4 | 17/5 | 1/5 | -22/5 |
| x2 | 2 | 0 | 1 |
| -F | -27/5 | -1/5 | -3/5 |
F опт = 27/5
XT ={ 7/5, 2 , 0 , 17/5 , 0}
Введём дополнительное ограничение на x1
x1 ≤ [ 7/5]
x1 ≥ [7/5] + 1
x1 ≤ 1
x1 ≥ 2
Задача 1
F = x1 + 2x2 à min
 5x1 + 7x2 ≤ 21
5x1 + 7x2 ≤ 21
-x1 + 3x2 ≤ 8
|
|
|
x2 ≤ 2
x1 ≥ 2
x1,x2 ≥ 0
Эта задача решения не имеет.
Задача 2
F = x1 + 2x2 à min
 5x1 + 7x2 ≤ 21
5x1 + 7x2 ≤ 21
-x1 + 3x2 ≤ 8
x2 ≤ 2
x1 ≤ 1
x1,x2 ≥ 0
 x3 = 21 – ( 5x1 + 7x2 )
x3 = 21 – ( 5x1 + 7x2 )
x4 = 8 – ( -x1 + 3x2 )
x5 = 2 – (x2 )
x6 = 1 – ( x1 )
 -F = 0 – ( x1 + 2x2 ) à min
-F = 0 – ( x1 + 2x2 ) à min
| β | x1 | x2 | |
| x3 | 21 -14 | 5 0 | 7 -7 |
| x4 | 8 -6 | -1 0 | 3 -3 |
 x5 x5
| 2 2 | 0 0 | 1 1 |
| x6 | 1 0 | 1 0 | 0 0 |
| -F | 0 -4 | 1 0 | 2 -2 |
 λ = 1
λ = 1
| β | x1 | x5 | |
| x3 | 7 -5 | 5 -5 | -7 0 |
| x4 | 2 1 | -1 1 | -3 0 |
| x2 | 2 0 | 0 0 | 1 0 |
x6
| 1 1 | 1 1 | 0 0 |
| -F | -4 -1 | 1 -1 | -2 0 |
λ = 1
| β | x6 | x5 | |
| x3 | 2 | -5 | -7 |
| x4 | 3 | 1 | -3 |
| x2 | 2 | 0 | 1 |
| x1 | 1 | 1 | 0 |
| -F | -5 | -1 | -2 |
F опт = 5
XT ={ 1, 2 , 2 , 3 , 0 , 0}
Дерево ветвления задачи:
|
|
|
 F =129/22
F =129/22







 F=27/5
F=27/5
F =5
4. Решение задачи булевского программирования о распределении капиталовложения.
4.2Булевское программирование. МетодБаллаша
Задание:
| Вариант | Проект | Расходы (млн. грн. в год) | Прибыль (млн. грн) | ||
| 1-й год | 2-й год | 3-й год | |||
| 19 | 1 | 4 | 6 | 3 | 10 |
| 2 | 9 | 7 | 8 | 15 | |
| 3 | 7 | 9 | 9 | 10 | |
| 4 | 5 | 5 | 6 | 25 | |
| 5 | 6 | 4 | 6 | 20 | |
| Доступный капитал | 30 | 30 | 30 | ||
Решение задач с булевыми переменными можно производить методом ветвей и границ, как с обычными целочисленными переменными, для которых заданы граничные условия 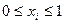 . Однако применение такого метода для данных задач в ряде случаев оказывается нецелесообразным. Существуют специальные методы частичного перебора для решения таких задач, наиболее совершенный из них называется аддитивным алгоритмом Баллаша с фильтром.
. Однако применение такого метода для данных задач в ряде случаев оказывается нецелесообразным. Существуют специальные методы частичного перебора для решения таких задач, наиболее совершенный из них называется аддитивным алгоритмом Баллаша с фильтром.
Суть этого метода сводится к следующему:
1) расположить переменные по возрастанию коэффициентов при них в целевой функции;
2) принять некоторый набор значений X, удовлетворяющий всем ограничениям;
3) значение целевой функции при удовлетворении п. 2 принять в качестве дополнительного фильтрующего ограничения (фильтра);
4) методом перебора X определить значение фильтрующего ограничения и проверить удовлетворение его заданным ограничениям;
|
|
|
5) если при некотором наборе X значение фильтрующего ограничения окажется для целевой функции лучшим, следует от первоначального набора перейти к новому и продолжить процедуру.
Составим математическую модель данной ЗЛП с булевскими переменными
1: 4x1 + 9x2 + 7x3+ 5x4+6x5 ≤ 30
2: 6x1 + 7x2 + 9x3 + 5x4 + 4x5 ≤ 30
3: 3x1+ 8x2 + 9x3 + 6x4 + 6x5 ≤ 30
F = 10x1 + 15x2 + 10x3 + 25x4 + 20x5 à max
Примем значение целевой функции на наборе 00000 за фильтрующее.
| № | X1 | X2 | X3 | X4 | X5 | Выполнение ограничений | ||||
| F | 1 | 2 | 3 | Fф | ||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | + | + | + | Fф=0 |
| 2 | 0 | 0 | 0 | 0 | 1 | 20 | + | + | + | 20 |
| 3 | 0 | 0 | 0 | 1 | 0 | 25 | + | + | + | 25 |
| 4 | 0 | 0 | 0 | 1 | 1 | 45 | + | + | + | 45 |
| 5 | 0 | 0 | 1 | 0 | 0 | 10 | - | |||
| 6 | 0 | 0 | 1 | 0 | 1 | 30 | - | |||
| 7 | 0 | 0 | 1 | 1 | 0 | 35 | - | |||
| 8 | 0 | 0 | 1 | 1 | 1 | 55 | + | + | + | 55 |
| 9 | 0 | 1 | 0 | 0 | 0 | 15 | - | |||
| 10 | 0 | 1 | 0 | 0 | 1 | 35 | - | |||
| 11 | 0 | 1 | 0 | 1 | 0 | 40 | - | |||
| 12 | 0 | 1 | 0 | 1 | 1 | 60 | + | + | + | 60 |
| 13 | 0 | 1 | 1 | 0 | 0 | 25 | - | |||
| 14 | 0 | 1 | 1 | 0 | 1 | 45 | - | |||
| 15 | 0 | 1 | 1 | 1 | 0 | 50 | - | |||
| 16 | 0 | 1 | 1 | 1 | 1 | 70 | + | + | + | 70 |
| 17 | 1 | 0 | 0 | 0 | 0 | 10 | - | |||
| 18 | 1 | 0 | 0 | 0 | 1 | 30 | - | |||
| 19 | 1 | 0 | 0 | 1 | 0 | 35 | - | |||
| 20 | 1 | 0 | 0 | 1 | 1 | 55 | - | |||
| 21 | 1 | 0 | 1 | 0 | 0 | 20 | - | |||
| 22 | 1 | 0 | 1 | 0 | 1 | 40 | - | |||
| 23 | 1 | 0 | 1 | 1 | 0 | 45 | - | |||
| 24 | 1 | 0 | 1 | 1 | 1 | 65 | - | |||
| 25 | 1 | 1 | 0 | 0 | 0 | 25 | - | |||
| 26 | 1 | 1 | 0 | 0 | 1 | 45 | - | |||
| 27 | 1 | 1 | 0 | 1 | 0 | 50 | - | |||
| 28 | 1 | 1 | 0 | 1 | 1 | 70 | - | |||
| 29 | 1 | 1 | 1 | 0 | 0 | 35 | - | |||
| 30 | 1 | 1 | 1 | 0 | 1 | 55 | - | |||
| 31 | 1 | 1 | 1 | 1 | 0 | 60 | - | |||
| 32 | 1 | 1 | 1 | 1 | 1 | 80 | - | - | ||
|
|
|
Фильтрующее ограничение:
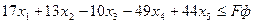
Максимальное значение 70 функция достигает на наборе 01111. С помошью фильтра Баллаша колличество вычислений было сокращено на 39%.
Поиск локального минимума метом одномерной оптимизации
Метод дихотомии ( деление отрезка пополам ).
Основная идея метода состоит в том, что на каждой итерации вычисляются значения 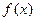 только в двух точках
только в двух точках 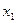 и
и 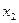 . Точки
. Точки 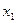 и
и 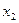 располагаются симметрично относительно середины текущего отрезка
располагаются симметрично относительно середины текущего отрезка 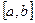 и разнесены между собой ровно на половину этого отрезка. Поэтому на каждой итерации в силу унимодальности функции из рассмотрения исключается ровно половина текущего отрезка поиска.
и разнесены между собой ровно на половину этого отрезка. Поэтому на каждой итерации в силу унимодальности функции из рассмотрения исключается ровно половина текущего отрезка поиска.
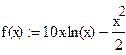
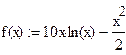
Проведем вычисление функции этим методом до тех пор пока длина уменьшаемого отрезка 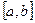 не станет меньше точности e=0.05, для этого потребуется примерно четыре итерации.
не станет меньше точности e=0.05, для этого потребуется примерно четыре итерации.
1:
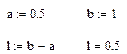
Найдем длину интервала
Выберем точки, равноотстоящие от концов заданного интервала
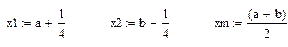
Теперь не обходимо вычислить значение функции в выбранных точках
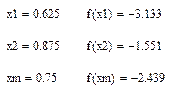
Как видно из вычисленных значений точка x1 является экстремумом из выбранных нами значений на этом шаге, а значит концом отрезка становиться середина, тем самым мы отсекаем половину отрезка, а бывшая точка x1 становиться серединой нового отрезка

Так как длина полученного отрезка после первой итерации больше е

то мы переходим ко второй итерации с новыми значениями, аналогично повторяя первую.
2:

 Условия окончания не выполнятся переходим к следующей итерации.
Условия окончания не выполнятся переходим к следующей итерации.
3:

4:
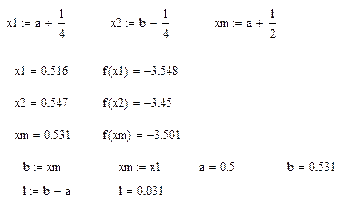
Полученное значение на этой итерации устраивает нас как экстремум функции вычисленный методом дихотомии, но для более точного вычисления экстремума продолжим решение этой задачи методом золотого сечения в следующем разделе.
Для более наглядного представления проделанных выше действий можно свести результаты в таблицу:
| Шаг | Левая граница | Правая граница | Точка экстремума | Значение экстремума |
| 1 | 0.5 | 1 | 0.625 | -3.133 |
| 2 | 0.5 | 0.75 | 0.563 | -3.395 |
| 3 | 0.5 | 0.625 | 0.531 | -3.501 |
| 4 | 0.5 | 0.563 | 0.516 | -3.548 |
Дата добавления: 2018-10-27; просмотров: 182; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
