Тема 2.2 Элементы математической статистики.
В результате изучения темы студент должен знать:
· Область применения и задачи математической статистики.
· Элементы выборки, формирование вариационного ряда.
· Совокупность объектов. Генеральная совокупность. Выборочная совокупность. Способы отбора. Статистические распределения.
Практическое занятие:
1. Решение задач математической статистики.
Вопросы для самоконтроля:
1. Формулы: перестановок, сочетаний, размещений.
2. Понятие математической статистики.
3. Среднее арифметическое.
4. Мода.
5. Медиана.
6. Размах.
Рекомендуемая литература:
Богомолов Н.В., Самойленко П.И. «Математика», - глава 17. стр. 382-386
Тема 2.3 Элементы дискретной математики.
В результате изучения темы студент должен знать:
· Основные характеристики теории графов.
· Матричные и числовые характеристики графов.
· Прикладные задачи и алгоритмы анализа графов.
Практическое занятие:
1. Решение задач по теории графов.
Вопросы для самоконтроля:
· Определение графа и его элементы.
· Ориентированный и неориентированный графы.
· Связный и несвязный граф.
· Простой граф.
· Дерево-граф.
Раздел 3. Элементы линейной алгебры и теории комплексных чисел.
Тема 3.1 Элементы линейной алгебры.
В результате изучения темы студент должен знать:
· Определение матрицы и её обозначения. Виды матриц. Определитель матрицы. Уравнение с одной переменной. Линейные уравнения.
· Метод Гаусса решения систем линейных уравнений.
· Использование системы линейных уравнений при решении экономических задач.
Практическое занятие:
1. «Решение систем линейных уравнений».
Вопросы для самоконтроля:
· Способ сложения.
· Способ подстановки.
· Графический способ решения систем уравнений.
· Метод Гаусса для решения систем линейных уравнений.
Рекомендуемая литература:
Богомолов Н.В., Самойленко П.И. «Математика», - глава 1, стр. 39-57
Тема 3.2. Комплексные числа.
В результате изучения темы студент должен знать:
· Понятие комплексного числа. Действительную и мнимую части комплексного числа.
· Аргумент и модуль комплексного числа.
· Геометрическую и тригонометрическую формы записи комплексных чисел.
· Правила выполнения операций с комплексными числами.
Практическое занятие:
1. Решение задач по выполнению арифметических действий с комплексными числами.
Вопросы для самоконтроля:
· Что принято за мнимую единицу?
· Какое число называется комплексным числом?
· Какие комплексные числа называются сопряженными, противоположными?
· Как найти i в любой степени?
· Как изображается геометрически комплексное число?
· Чему равен модуль комплексного числа?
· Как находится аргумент комплексного числа?
Рекомендуемая литература:
Богомолов Н.В., Самойленко П.И. «Математика», - глава 1, стр. 8-11
Интернет-ресурс http://www.youtube.com/watch?v=dZPRzB1Nj08 (Лекция 6. Комплексные числа (часть 1))
Методические указания по выполнению контрольной работы.
Заочная форма обучения предполагает самостоятельную работу студента над учебным материалом: чтение учебников, решение задач, выполнение контрольных заданий. Однако, в случае возникновения затруднений при самостоятельном изучении материала, студент может обратиться к преподавателю математики для получения устной консультации.
Студенты-заочники, в соответствии с ФГОС СПО изучают курс математики в течение одного года обучения и выполняют одну контрольную работу.
При выполнении контрольной работы студент должен руководствоваться следующими указаниями:
1. Контрольная работа выполняется в отдельной тетради в клетку, на титульном листе которой, должны быть ясно написаны фамилия студента, его инициалы, полный шифр, курс, специальность, домашний адрес студента.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. Ход решения каждой задачи студент обязан оформить аккуратно, в полном соответствии с порядком решения типичной задачи, приведенной в данных методических указаниях.
4. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единиц масштаба.
5. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
6. Контрольная работа выполняется самостоятельно.
7. В случае незачета по контрольной работе студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работу на повторную проверку.
8. Студент выполняет тот вариант, который совпадает с последней цифрой его учебного шифра в соответствии с таблицей.
| № варианта | Номера заданий | |||||
| 1 | 1 | 21 | 31 | 41 | 51 | 61 |
| 2 | 2 | 22 | 32 | 42 | 52 | 62 |
| 3 | 3 | 23 | 33 | 43 | 53 | 63 |
| 4 | 4 | 24 | 34 | 44 | 54 | 64 |
| 5 | 5 | 25 | 35 | 45 | 55 | 65 |
| 6 | 6 | 26 | 36 | 46 | 56 | 66 |
| 7 | 7 | 27 | 37 | 47 | 57 | 67 |
| 8 | 8 | 28 | 38 | 48 | 58 | 68 |
| 9 | 9 | 29 | 39 | 49 | 59 | 69 |
| 10 | 10 | 30 | 40 | 50 | 60 | 70 |
Задание № 1
В задачах 1-10 ответить письменно на теоретические вопросы.
1. Определение предела функции. Правила раскрытия неопределенностей типа 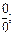
 .
.
2. Определение производной функции. Геометрический смысл производной функции.
3. Определение производной функции. Физический смысл производной функции.
4. Определение дифференциала функции. Определение дифференцирования. Правила дифференцирования.
5. Определение дифференцирования. Формулы дифференцирования.
6. Определение первообразной функции. Теорема о существовании бесконечного множества первообразных. Геометрическое изображение первообразных.
7. Определение неопределенного интеграла. Свойства интеграла. Таблица неопределенных интегралов.
8. Определение криволинейной трапеции. Площадь криволинейной трапеции. Формула Ньютона-Лейбница.
9. Определение определенного интеграла. Свойства определенного интеграла.
10. Понятие о дифференциальных уравнениях. Определение дифференциального уравнения, порядок дифференциального уравнения, решение, общее решение, частное решение, интегральная кривая. Дифференциальное уравнение первого порядка.
Задание № 2
В задачах 11-20 вычислить пределы функции:
21. a) 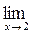 (2x2-3x+4); б)
(2x2-3x+4); б) 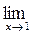
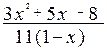 ; в)
; в) 
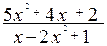 ;
;
22. a) 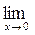 (3x3+x2+8x+10); б)
(3x3+x2+8x+10); б) 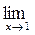
 ; в)
; в) 
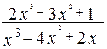 ;
;
23. a)  (x3-x2+1); б)
(x3-x2+1); б) 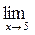
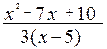 ; в)
; в) 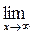
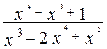 ;
;
24. a) 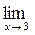 (2x2-8x+4); б)
(2x2-8x+4); б) 
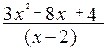 ; в)
; в) 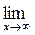
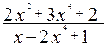 ;
;
25. a) 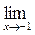 (2x2-4x+5); б)
(2x2-4x+5); б) 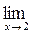
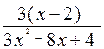 ; в)
; в) 
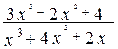 ;
;
26. a)  (-3x2+4x-8); б)
(-3x2+4x-8); б) 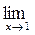
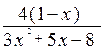 ; в)
; в) 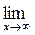
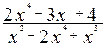 ;
;
27. a)  (4x4-5x2+4); б)
(4x4-5x2+4); б) 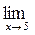
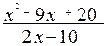 ; в)
; в) 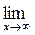
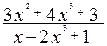 ;
;
28. a) 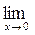 (4x3-2x-1); б)
(4x3-2x-1); б) 
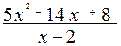 ; в)
; в) 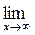
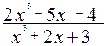 ;
;
29. a)  (2x2+4x); б)
(2x2+4x); б) 
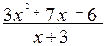 ; в)
; в) 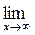
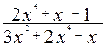 ;
;
30. a)  (x3-x2+1); б)
(x3-x2+1); б) 
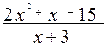 ; в)
; в) 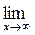
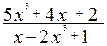 .
.
Решение типовых примеров
Вычислить пределы:
1) 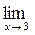 (4x-x2+8).
(4x-x2+8).
В этом примере необходимо провести непосредственную подстановку.
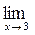 (4x-x2+8)=4·3-32+8=12-9+8=11
(4x-x2+8)=4·3-32+8=12-9+8=11
2) 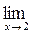
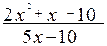 =
= 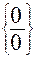 .
.
Непосредственная подстановка приводит к неопределенности типа 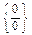 . Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель (х-2).
. Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель (х-2).
Числитель: 2х2+х-10=2(х-2)(х+ 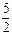 )
)
2х2+х-10=0
D=1-4·2(-10)=1+80=81
x1= 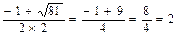 x2=
x2= 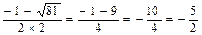
Используемые формулы:
– расположение квадратного трехчлена на множители ax2+bx+c=a(x-x1)(x-x2), где х1, х2 корни квадратного уравнения ax2+bx+c=0.
– D=b2-4ac
x1= 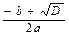 ; x2=
; x2= 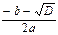
Знаменатель: 5х-10=5(х-2)

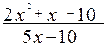 =
= 
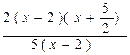 =
= 
 =
= 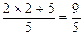
3) 
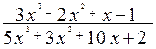 =
= 
В этом примере получается неопределенность вида 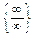 , избавиться от которой можно вынесением за скобки в числителе и в знаменателе дроби старшей степени переменной:
, избавиться от которой можно вынесением за скобки в числителе и в знаменателе дроби старшей степени переменной:

 =
= 

Задание № 3
В задачах 31-40 исследовать заданную функцию методами дифференциального исчисления и построить эскиз графика.
Исследование функций рекомендуется проводить по следующей схеме:
1) Найти область определения функции;
2) Найти производную функции;
3) Найти точки экстремума;
4) Определить промежутки монотонности функции;
5) Найти точки перегиба функции;
6) Определить промежутки выпуклости и вогнутости функции;
7) Найти значение функции в точках экстремума и перегиба;
8) Построить эскиз графика.
Задания:
31. у=2х3-9х2+12х-5,
32. у=х3-6х2+9х+1
33. у=х3-3х2-9х+10
34. у=х3+3х2-9х-10
35. у=х3+6х2+9х+2
36. у=2х3-3х2-12х+5
37. у=2х3+3х2-12х-8
38. у=2х3+9х2+12х+7
39. у=2х3-15х2+36х-32
40. у=2х3-15х2+24х+4
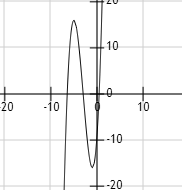
Решение типового примера: исследовать функциюу=х3+9х2+15х-9
1) Областью определения данной функции является все действительные значения аргумента х, т.е D(y)=R
2) Найдем производную функции y´=3x2+18x+15
3) Найдем точки экстремума, для этого приравняем производную к нулю.
3x2+18x+15=0, :/3 х2+6х+5=0 D=36-4·5=16; x1= 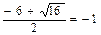 ; x2=
; x2= 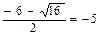
Значит функция имеет две критические точки х1=-1, х2=-5.
4) Найдем промежутки монотонности функции, для этого разбиваем область определения критическими точками на интервалы
 |  | ||
 + – +
+ – +
 |
–5 –1
т. max т. min
Определим знак производной на каждом интервале:
y´(0)=3·02+18·0+15=15>0, значит на интервале (-1;+ 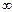 ) производная функции положительная, значение функции возрастает.
) производная функции положительная, значение функции возрастает.
y´(-2)=3·(-2)2+18·(-2)+15=-9<0, на промежутке (-5;-1) производная функции отрицательная, значения функции убывает.
y´(-6)=3·(-6)2+18·(-6)+15=30>0, на промежутке (- 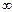 ;-5) производная функции положительная, значения функции возрастает.
;-5) производная функции положительная, значения функции возрастает.
Отсюда следует, что х1=-5 – точка максимума (max), х2=-1 – точка минимума (min).
5) Найдем точки перегиба функции, для этого найдем вторую производную функции и приравниваем ее к нулю:
y´´=6х+18 6х+18=0 6х=-18 х=-3 – критическая точка.
6) Определим промежутки выпуклости и вогнутости функции. Разобьем область определения на интервалы (- 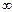 ;-3) и (-3;+
;-3) и (-3;+ 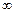 )
)


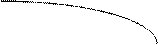
 – +
– +
 –3 (т. перегиба)
–3 (т. перегиба)
Определим знак второй производной на каждом интервале:
y´´(0)=6·0+18=18>0; y´´=6·(-4)+18=-6<0.
На промежутке (-3;+ 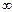 ) – функция выпуклая; а на промежутке (-
) – функция выпуклая; а на промежутке (- 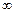 ;-3) – функция вогнутая, значит х=-3 – точка перегиба.
;-3) – функция вогнутая, значит х=-3 – точка перегиба.
7) Найдем значение функции в точках в точках экстремума и перегиба
ymax=y(-5)=((-5)3+9(-5)2+15(-5)-9)=16
ymin=y(-1)=((-1)3+9(-1)2+15(-1)-9)=-16
yперегиба=y(-3)=((-3)3+9(-3)2+15(-3)-9)=0
8) Построим эскиз графика с учетом предыдущих исследований
Задание № 4
В задачах 41-50 вычислить неопределенные интегралы, результат проверить дифференцированием.
41. а) 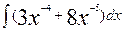 ; б)
; б)  .
.
42. а)  ; б)
; б) 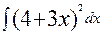 .
.
43. а) 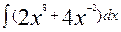 ; б)
; б) 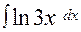 .
.
44. а) 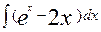 ; б)
; б) 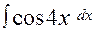 .
.
45. а) 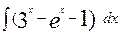 ; б)
; б) 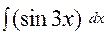 .
.
46. а) 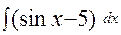 ; б)
; б) 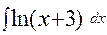 .
.
47. а) 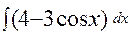 ; б)
; б)  .
.
48. а) 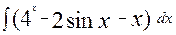 ; б)
; б) 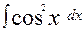 .
.
49. а) 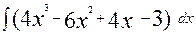 ; б)
; б) 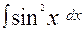 .
.
50. а) 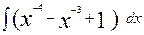 ; б)
; б) 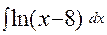 .
.
Решение типового примера
1) Найти неопределенные интегралы, результат проверить дифференцированием.
а) 
Проверка дифференцированием:
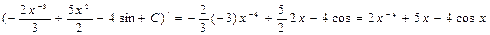
б) 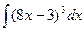
Применим подстановку
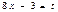
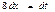
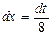

Проверка дифференцированием:
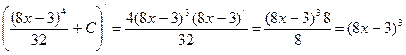
Используемые формулы: 
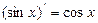
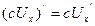

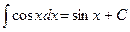
Задание № 5
В задачах 51-60 вычислить площадь фигуры, ограниченную заданными линиями:
51. y=x2, y=49.
52. y=x3, y=8.
53. y=x2+1, x= - 2, x= 2.
54. y=x2, y=64.
55. y=x+2, x=2, x=4.
56. y=x3+1, y=9.
57. y=x2+1, y=26.
58. y=2x, x=1, x=2.
59. y=x3+1, y=28.
60. y=x2+2, y=27.
Решение типового примера
Вычислить площадь фигуры, ограниченную заданными линиями:

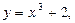
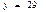 y
y




 29
29
 |
 2
2
 0 3 x
0 3 x
Найдем абсциссы точек пересечения заданных линий
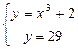 ;
; 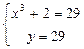 ;
; 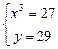 ;
; 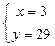
Площадь фигуры 
| |

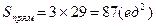
|
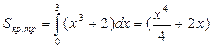

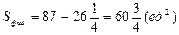
Ответ: площадь фигуры составляет 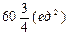
Используемые формулы: Ньютона-Лейбница
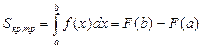
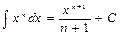
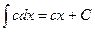
Задание № 6
В задачах 61-70 выполните арифметические действия над комплексными числами: z 1 и z 2
61. z1 = 3-5i и z2= -3+4i 62. z1 = 6-3i и z2 = - 5+3i
63. z1 = 4 +2i и z2 = - 4- i 64. z1 = - 4-3i и z2 = 5 - 2i
65. z1 = 8i -3 и z2 = 3 - 2i 66. z1 = 11- 2i и z2 = -8-8i
67. z1 = 5- 7 i и z2 = -4-5i 68. z1 =-3i -5 и z2 =-6-7 i
69. z 1 = 7+4i и z 2 = - 9+3i 70. z 1 = -2 – i и z 2 =7-3 i
Решение типового примера
Выполните арифметические действия над комплексными числами:
z 1 = – 2 + 3 i и z 2 = 4 – 5 i
Решение:
z1 + z2 = (– 2 + 3i) + (4 – 5i) = (– 2 + 4) + i (3 – 5) = 2 – 2i
z1 – z2 = (– 2 + 3i) – (4 – 5i) = (– 2 – 4) + i (3–(– 5 )) = – 6 + 8i
z1 · z2 = (– 2 + 3i) (4 – 5i) = – 2 · 4 + 3i · 4 + (– 2) (– 5i) + 3i (– 5i) =
= 8 + 12i + 10i – 15i2 = [т . к. i2 = – 1] = 8 + 22i + 15 = 23 + 22i
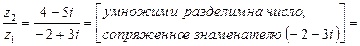
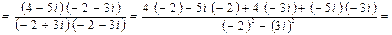
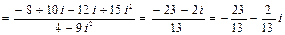
Задание № 7
Дата добавления: 2018-10-26; просмотров: 334; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
