Утверждение 1. ( О структуре общего решения неоднородного уравнения).
Если  – общее решение однородного уравнения (3), а
– общее решение однородного уравнения (3), а 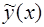 – какое-либо частное решение неоднородного уравнения (1), то
– какое-либо частное решение неоднородного уравнения (1), то
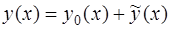 (4)
(4)
есть общее решение неоднородного уравнения (1).
Отсюда следует, что построение общего решения неоднородного уравнения состоит из двух этапов. Сначала нужно найти общее решение  соответствующего однородного уравнения, а затем найти какое-либо частное решение
соответствующего однородного уравнения, а затем найти какое-либо частное решение 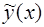 неоднородного уравнения.
неоднородного уравнения.
I. Нахождение общего решения линейного однородного уравнения с постоянными коэффициентами (метод Эйлера)
Определение . Будем говорить, что два решения 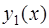 и
и  линейного однородного уравнения (3) линейно независимы на промежутке
линейного однородного уравнения (3) линейно независимы на промежутке 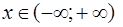 , если их отношение
, если их отношение 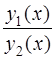 не равно тождественно константе.
не равно тождественно константе.
Тогда имеет место следующее утверждение.
Утверждение 2. ( О структуре общего решения однородного уравнения).
Если 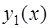 и
и 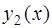 – два линейно независимых решения уравнения (3), то их линейная комбинация
– два линейно независимых решения уравнения (3), то их линейная комбинация
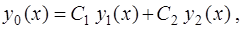 (5)
(5)
где 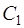 и
и  – произвольные постоянные, есть общее решение линейного однородного уравнения (3).
– произвольные постоянные, есть общее решение линейного однородного уравнения (3).
Решение уравнения (3)

где  и
и  – вещественные числа, будем искать в виде
– вещественные числа, будем искать в виде
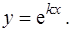 (6)
(6)
Постоянная 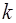 подлежит определению.
подлежит определению.
Так как 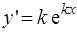 и
и  , то подстановка полученных выражений производных в уравнение (3) приводит к равенству
, то подстановка полученных выражений производных в уравнение (3) приводит к равенству
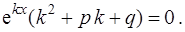 Так как
Так как 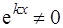 , то последнее равенство выполняется, если
, то последнее равенство выполняется, если
|
|
|
 (7)
(7)
Таким образом, функция 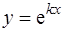 является решением дифференциального уравнения (3), если постоянная
является решением дифференциального уравнения (3), если постоянная 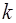 является корнем квадратного уравнения (7).
является корнем квадратного уравнения (7).
Уравнение (7) называетсяхарактеристическим уравнением дифференциального уравнения (3).
Напомним формулу для определения двух корней 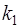 и
и 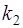 квадратного уравнения (7). Пусть дискриминант
квадратного уравнения (7). Пусть дискриминант 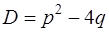 , тогда
, тогда
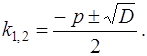 (8)
(8)
При решении квадратного уравнения (7) возможны три случая в зависимости от знака дискриминанта 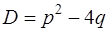 :
:
1) корни уравнения  и
и  вещественные и различные
вещественные и различные 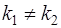

2) корни уравнения  и
и 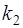 вещественные и равные
вещественные и равные 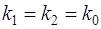
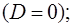
3) корни уравнения  и
и 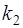 – комплексно сопряженные числа
– комплексно сопряженные числа 
Рассмотрим каждый из этих случаев.
1. Корни уравнения  и
и 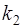 вещественные и различные
вещественные и различные 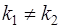 . Тогда уравнение(3) имеет два решения
. Тогда уравнение(3) имеет два решения 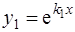 и
и 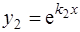 . Они линейно независимы, так как
. Они линейно независимы, так как
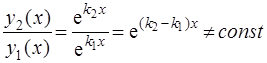
и, следовательно, общее решение уравнения (3) имеет вид
 (9)
(9)
где 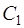 и
и 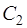 – произвольные постоянные.
– произвольные постоянные.
2. Пусть корни характеристического уравнения 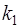 и
и 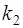 вещественные и равные
вещественные и равные 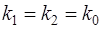 . Тогда линейное однородное уравнение (3) имеет два линейно независимых решения
. Тогда линейное однородное уравнение (3) имеет два линейно независимых решения  и
и 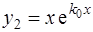 (см. [2] и [4]) и, следовательно, общее решение уравнения (3) имеет вид
(см. [2] и [4]) и, следовательно, общее решение уравнения (3) имеет вид
|
|
|
 (10)
(10)
где  и
и 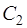 – произвольные постоянные.
– произвольные постоянные.
3. Пусть корни характеристического уравнения 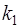 и
и 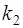 – комплексно сопряженные числа
– комплексно сопряженные числа 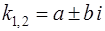 , где
, где  и
и 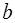 – вещественные числа, причем
– вещественные числа, причем 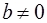 ,
, 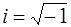 – мнимая единица (см. [2] и [4]). Тогда линейное однородное уравнение (3) имеет два линейно независимых решения
– мнимая единица (см. [2] и [4]). Тогда линейное однородное уравнение (3) имеет два линейно независимых решения 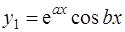 и
и 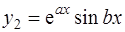 и, следовательно, общее решение уравнения (3) имеет вид
и, следовательно, общее решение уравнения (3) имеет вид
 (11)
(11)
где  и
и  – произвольные постоянные.
– произвольные постоянные.
II. Построение частного решения линейного неоднородного уравнения со специальной правой частью. Метод неопределенных коэффициентов
Этот метод применим тогда, когда в правой части уравнения (1) стоит функция специального вида (2). В этом случае частное решение 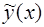 уравнения может быть найдено в соответствии с видом его правой части.
уравнения может быть найдено в соответствии с видом его правой части.
Рассмотрим здесь два частных варианта специальных правых частей.
1. Пусть в формуле (2) число 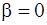 , тогда уравнение (1) имеет вид
, тогда уравнение (1) имеет вид
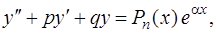 (12)
(12)
где 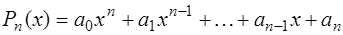 – многочлен степени
– многочлен степени 
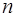 , а вещественное число
, а вещественное число 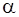 является контрольным числом.
является контрольным числом.
Уравнению (12) соответствует однородное уравнение
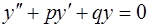
с характеристическим уравнением
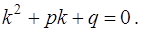 (13)
(13)
Пусть 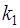 и
и 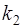 его корни.
его корни.
|
|
|
Имеет место следующее утверждение (см. [2]).
Утверждение 3.
Частное решение уравнения (12) следует искать в виде:
a) если контрольное число 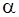 не является корнем характеристического уравнения (13), т.е.
не является корнем характеристического уравнения (13), т.е. 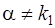 и
и 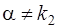 , то
, то
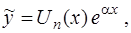
где 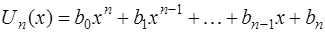 – многочлен той же степени
– многочлен той же степени 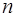 , что и многочлен
, что и многочлен  , с коэффициентами
, с коэффициентами  , подлежащими дальнейшему определению;
, подлежащими дальнейшему определению;
b) если контрольное число 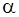 является простым корнем характеристического уравнения (13), т.е.
является простым корнем характеристического уравнения (13), т.е. 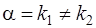 или
или  , то
, то
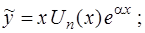
c) если контрольное число 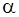 является кратным корнем характеристического уравнения (13), т.е.
является кратным корнем характеристического уравнения (13), т.е. 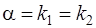 , то
, то
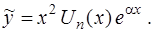
Приведем сводную таблицу.
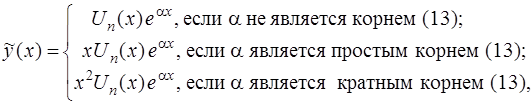
где 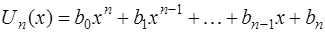 – многочлен той же степени
– многочлен той же степени 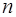 , что и многочлен
, что и многочлен 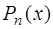 , с коэффициентами
, с коэффициентами  , подлежащими дальнейшему определению.
, подлежащими дальнейшему определению.
Коэффициенты 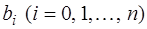 многочлена
многочлена 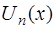 должны быть такими, чтобы функция
должны быть такими, чтобы функция 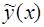 удовлетворяла уравнению (12). Поэтому для их отыскания используют следующий алгоритм.
удовлетворяла уравнению (12). Поэтому для их отыскания используют следующий алгоритм.
С помощью утверждения 3 устанавливается вид частного решения 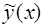 .
.
Затем определяются производные 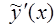 и
и  . Решение
. Решение 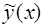 и его производные с неопределенными пока коэффициентами подставляются в уравнение (12) и обе его части сокращаются на
и его производные с неопределенными пока коэффициентами подставляются в уравнение (12) и обе его части сокращаются на  .
.
Далее, мы определяем коэффициенты  , исходя из тождественного равенства двух многочленов, стоящих в левой и правой частях уравнения (12)
, исходя из тождественного равенства двух многочленов, стоящих в левой и правой частях уравнения (12)
|
|
|
(два многочлена равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях переменной  ).
).
Решение задачи № 4
Найдем общее решение уравнения
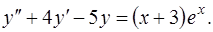 (14)
(14)
Это линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Его общее решение ищем в виде 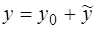 . Неоднородному уравнению (14) соответствует однородное уравнение
. Неоднородному уравнению (14) соответствует однородное уравнение
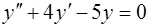 . (15)
. (15)
Функция 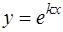 является решением уравнения (15), если
является решением уравнения (15), если  есть корень характеристического уравнения
есть корень характеристического уравнения
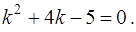 (16)
(16)
Оно имеет корни 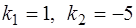 (вещественные и различные). Следовательно, общее решение однородного уравнения (15) имеет вид
(вещественные и различные). Следовательно, общее решение однородного уравнения (15) имеет вид
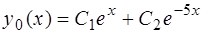 .
.
Построим теперь частное решение 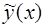 уравнения (14). В нашем случае правая часть уравнения (14)
уравнения (14). В нашем случае правая часть уравнения (14)

Сравнивая два последних выражения, получаем 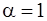 и
и 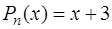 – многочлен первой степени,
– многочлен первой степени,  .
.
Поскольку контрольное число 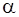 совпадает с корнем характеристического уравнения
совпадает с корнем характеристического уравнения 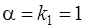 (
( 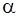 – простой корень характеристического уравнения (16)), частное решение уравнения (14) следует искать в виде
– простой корень характеристического уравнения (16)), частное решение уравнения (14) следует искать в виде
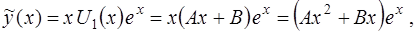
где коэффициенты 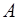 и
и 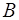 подлежат определению.
подлежат определению.
Чтобы найти 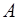 и
и 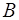 , подставим
, подставим  и его производные в исходное уравнение (14). Здесь при вычислении
и его производные в исходное уравнение (14). Здесь при вычислении 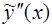 удобно воспользоваться формулой
удобно воспользоваться формулой 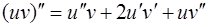 .
.
Итак,

и левая часть уравнения (14) принимает вид
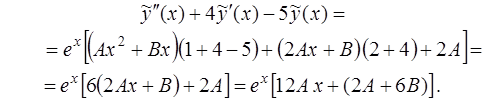
В результате для определения коэффициентов 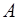 и
и 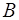 получаем уравнение
получаем уравнение
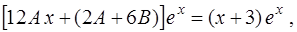
обе части которого можно сократить на множитель  .
.
Коэффициенты 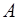 и
и 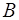 должны быть такими, чтобы обе части уравнения (14) были тождественно равны друг другу, т.е.
должны быть такими, чтобы обе части уравнения (14) были тождественно равны друг другу, т.е.
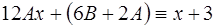 . (17)
. (17)
Тождество (17) выполняется тогда и только тогда, когда слева и справа стоят одинаковые коэффициенты при одинаковых степенях 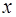 :
:
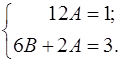
Следовательно, 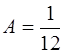 ,
, 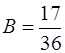 , а
, а 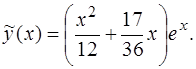
Таким образом, общее решение уравнения (14) имеет вид

Ответ. Общим решением уравнения (14) является функция

определенная на интервале 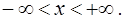
2. Рассмотрим решение линейного неоднородного уравнения (1) со специальной правой частью

Предполагается, что контрольные числа  мнимые, т. е.
мнимые, т. е.  , а
, а 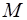 и
и  – вещественные числа, заданные многочлены нулевой степени (см. формулу (2)).
– вещественные числа, заданные многочлены нулевой степени (см. формулу (2)).
Уравнение (1) в этом случае принимает вид
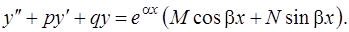 (18)
(18)
Уравнению (18) соответствует однородное уравнение

с характеристическим уравнением
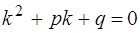 . (19)
. (19)
Пусть 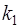 и
и 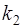 его корни.
его корни.
Имеет место следующее утверждение (см. [2]).
Утверждение 4.
Частное решение уравнения (18) следует искать в виде:
a) если контрольные числа  не являются корнями характеристического уравнения (19), т.е.
не являются корнями характеристического уравнения (19), т.е.  , то
, то
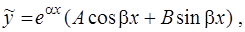
где 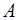 и
и 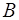 – неизвестные числа, подлежащие дальнейшему определению;
– неизвестные числа, подлежащие дальнейшему определению;
b) если контрольные числа  являются корнями характеристического уравнения (19), т.е.
являются корнями характеристического уравнения (19), т.е. 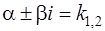 , то
, то
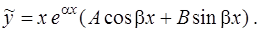
Заметим, что искомое частное решение всегда содержит оба слагаемых 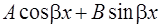 вне зависимости от того, содержит ли функция, стоящая в правой части уравнения (18), одновременно
вне зависимости от того, содержит ли функция, стоящая в правой части уравнения (18), одновременно  и
и 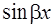 .
.
Числа  и
и 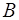 определяются непосредственной подстановкой решения
определяются непосредственной подстановкой решения 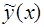 и его производных в уравнение (18).
и его производных в уравнение (18).
Для того чтобы уравнение превратилось в тождество, приравняем коэффициенты при 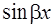 и
и 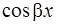 в его левой и правой частях.
в его левой и правой частях.
В результате получим систему линейных уравнений для нахождения 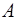 и
и 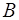 .
.
Решение задачи № 5
Решить задачу Коши:
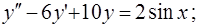 (20)
(20)
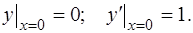 (21)
(21)
Это линейное неоднородное уравнение второго порядка с постоянными коэффициентами.
Его общее решение ищем в виде 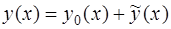 .
.
Неоднородному уравнению (20) соответствует однородное уравнение
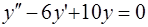 (22)
(22)
Функция 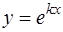 является решением уравнения (22) в том случае, если
является решением уравнения (22) в том случае, если  есть корень характеристического уравнения
есть корень характеристического уравнения
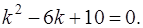 (23)
(23)
Оно имеет два комплексно сопряженных корня
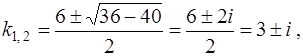
т.е. 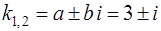 , где
, где  и
и 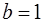 .
.
Следовательно, общее решение однородного уравнения (22) в соответствии с формулой (11) имеет вид
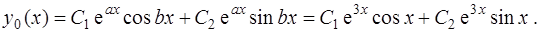
Построим теперь частное решение 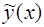 уравнения (20).
уравнения (20).
Для уравнения (20)

Отсюда имеем 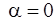 ,
, 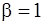 ,
, 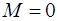 и
и 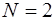 .
.
Частное решение 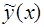 следует искать в виде
следует искать в виде

поскольку контрольные числа 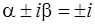 не совпадают с корнями
не совпадают с корнями 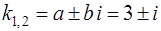 характеристического уравнения (23).
характеристического уравнения (23).
Коэффициенты 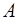 и
и 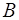 подлежат определению.
подлежат определению.
Вычислим первую и вторую производные функции 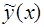
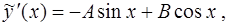
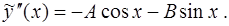
После подстановки  ,
,  и
и 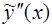 в левую часть (20) имеем:
в левую часть (20) имеем:
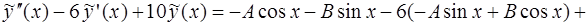
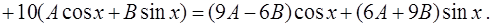
Следовательно, 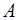 и
и 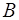 должны обеспечивать выполнение тождества
должны обеспечивать выполнение тождества
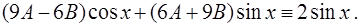
Отсюда, приравнивая коэффициенты при  и
и  в его левой и правой частях, получим систему линейных уравнений с двумя неизвестными
в его левой и правой частях, получим систему линейных уравнений с двумя неизвестными  и
и 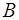 :
:
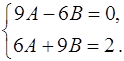
Решая эту систему, находим

Общее решение уравнения (20) имеет вид
 (24)
(24)
Найдем теперь значения постоянных 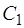 и
и 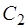 , при которых выполняются начальные условия (21). Согласно первому из них
, при которых выполняются начальные условия (21). Согласно первому из них
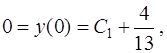
откуда  .
.
Продифференцируем общее решение (24)
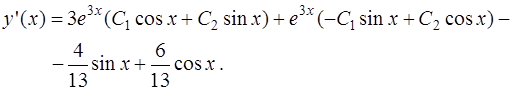
Согласно второму из равенств (21) имеем
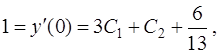
откуда найдем  .
.
Подставив найденные значения 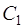 и
и 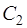 в общее решение (24), получаем искомое частное решение
в общее решение (24), получаем искомое частное решение
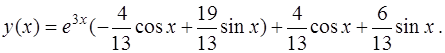
Ответ.
Решением задачи Коши (20),(21) является функция 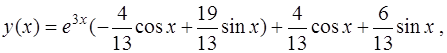
определенная на интервале 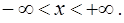
Дата добавления: 2018-10-26; просмотров: 272; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
