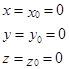Пример решения второй задачи динамики
ЛЕКЦИЯ 1
ДИНАМИКА
Динамика - раздел кинетики общей механики, в котором изучается механическое движение в связи с силами, приложенными к движущимся объектам.
В динамике (в большинстве случаев), как и в статике, применяется принцип освобождения от связей: несвободную материальную точку (систему), движение которой обуславливают связи, можно рассматривать как свободную, если действие отброшенных связей заменять реакциями связей.
Законы динамики 
Первый закон (закон инерции): изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение совершаемое точкой при отсутствии сил, называется движением по инерции.
Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы, а именно: произведение массы материальной точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.
Математически этот закон выражается векторным равенством
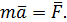
Между модулями ускорения и силы имеет место зависимость
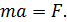
Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона видно, что мерой инертности материальной точки является ее масса, поскольку при действии данной силы точка, масса которой больше, т. е. более инертная, получит меньшее ускорение и наоборот.
Третий закон (закон равенство действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
Дифференциальные уравнения движения материальной точки
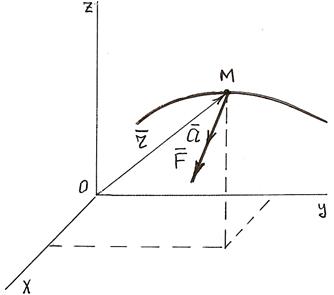
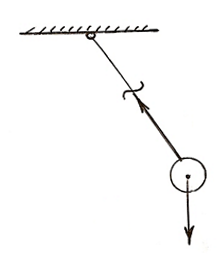
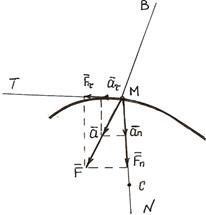
Пусть материальная точка M массой m движется относительно инерциальной системы отсчета под действием некоторой силы 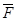 .
.
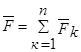
- равнодействующая активных сил и реакций связей.
Применим основной закон динамики (2-й закон Ньютона)
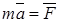 . .
| (1) |
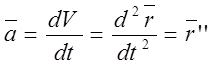
| (2) |

| |
 - дифференциальное уравнение движения
- дифференциальное уравнение движения
Материальной точки в векторной форме.
Проецируя (1) на оси декартовой системы координат, получим:

|
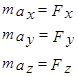
|
 ;
; 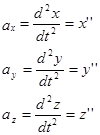 ;
;  ;
;
Если спроецировать (1) на естественные оси координат, получим:
|

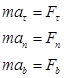 ;
; 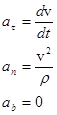 ;
; 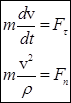
| |
Задачи динамики
Используя дифференциальные уравнения движения материальной точки можно решать две основные задачи динамики: прямую и обратную.
I -я (прямая) задача динамики .
Если известна масса точки и закон или уравнения движения (например, в декартовых координатах), то можно найти действующую на точку силу.
Например, уравнения движения в декартовой системе координат:
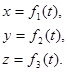 (1)
(1)
Дифференциальные уравнения движения в декартовых координатах:
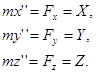
Модуль силы  ; направляющие косинусы
; направляющие косинусы
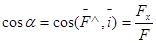 ,
,
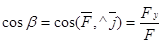 ,
,
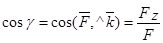 .
.
Т.о. для расчета силы необходимо дважды продифференцировать уравнения (или закон) движения (1) и домножить на массу.
Эта задача всегда доводится до конца и при решении трудностей не возникает.
II -я (обратная) задача динамики.
Если известна масса точки, сила, действующая на точку и начальные условия (начальные координаты, т.е. положение точки и начальная скорость), то можно определить закон движения точки (уравнения движения). Для этого необходимо составить и дважды проинтегрировать дифференциальные уравнения движения. Начальные условия позволяют определить постоянные интегрирования  .
.
Вторая задача значительно сложнее первой и часто возникают математические трудности.
Аргументы переменной силы
Силы, приложенные к материальной точке, могут быть:
а). Постоянными  (например, сила тяжести);
(например, сила тяжести);
б). Зависящими от времени 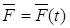 (вибрация, удар);
(вибрация, удар);
в). Зависящими от положения точки 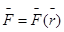 или
или  (силы притяжения и отталкивания);
(силы притяжения и отталкивания);
г). Зависящими от скорости 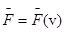
или  (силы сопротивления).
(силы сопротивления).
В общем случае силы могут зависеть от всех названных параметров, т.е.  .
.
Пример решения второй задачи динамики
Движение тела, брошенного под углом к горизонту
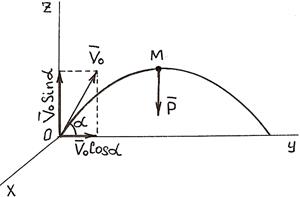
 Дано: Начальные условия: при
Дано: Начальные условия: при 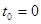
|
 (a)
(a)
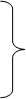 Опр.:
Опр.: 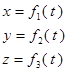
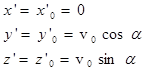 (б)
(б)
| Рассуждения | x | y | z | Примечания |
| Составим д.у.д. в проекциях на оси координат | mx’’=0 | my’'=0 | mz’’=-p=-mg | |
| Разделим на m | X’’=0 | Y’’=0 | Z’’=-g | |
| Произведем замену | 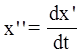
| 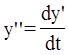
| 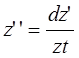
| |
| Разделим переменные и про интегрируем | X’=C1 | Y’=C2 | Z’’=-gt+C3 
| 1-е общие интегралы |
| Найдем C1, C2, C3 при н.у. (б) | C1=0 | C2= 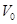 cosα cosα
| C3= 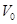 sinα sinα
| |
| Подставим C1, C2, C3 в первый общий интеграл | X’=0 (1) | Y’= V0cosα (2) | Z’=-gt+ V 0sinα (3) | Закон изменения проекций скоростей |
| Произведем замену | 
| 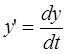
| 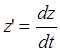
| |
| Разделим переменные и интегрируем | X= C4 | Y= 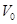 cosαt+C5 cosαt+C5
| 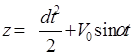 +C6 +C6
| 2-е общий интегрирование |
| Найдем C4, C5, C6 при н.у. (а) | C4 =0 | C5 =0 | C6 =0 | |
| Подставим C4, C5, C6 во второй общий интеграл | X=0 (4) | Y= 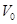 cosαt
(5) cosαt
(5)
|  (6)
(6)
| Уравнения движения точки |
Используя частные полученные интегралы (1)…(6) можно определить параметры тела брошенного под углом к горизонту: время полета, дальность, уравнение траектории и т.д.
Механическая система.
Дата добавления: 2018-10-26; просмотров: 588; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!