Определение криволинейного интеграла, его свойства
Рассмотрим гладкую пространственную кривую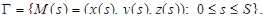 
параметром на которой выбрана переменная длина дуги s. Это означает, что длина дуги кривой от ее начала M(0) до точки M(s) равна s. Функции 
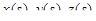непрерывны вместе со своими производными 
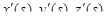на отрезке [0, S]. Единичный касательный вектор к кривой в точке M(s) имеет вид 
.
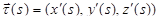Предположим, что на кривой Г задана вектор-функция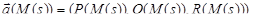 
, являющаяся непрерывной функцией параметра 
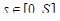. Умножив в каждой точке кривой значение вектор-функции 
скалярно на единичный касательный вектор 
, будем иметь непрерывную на отрезке [0, S] числовую функцию:
.
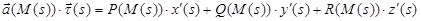Разобьем отрезок [0, S] произвольным образом точками 
. Длину отрезка 
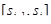обозначим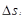 
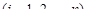. Отметим, что, по смыслу параметра s, 
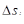есть длина дуги кривой между точкам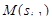и 
и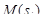 
. Выбрав произвольным образом точки 
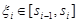, составим сумму
.
Эта сумма является интегральной суммой для непрерывной на отрезке [0, S] функции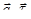 
. Поэтому при стремлении к нулю мелкости разбиений (мелкостью разбиения называется наибольшая из длин отрезков разбиения) последовательность таких сумм имеет своим пределом определенный интеграл 
. Этот интеграл называется криволинейным интегралом от вектор-функции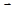 
по кривой Г и обозначается 
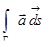или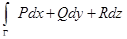 
.
Таким образом, по определению
.
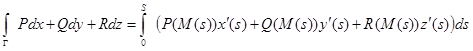Поскольку понятие криволинейного интеграла сводится к понятию определенного интеграла, для криволинейного интеграла сохраняются важнейшие свойства определенного интеграла: линейность, аддитивность и др.
|
|
|
1. Для любых непрерывных на Г вектор-функци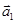й 
и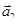 
и постоянных 
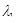и 
и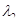меет место равенство:
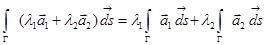
(линейность криволинейного интеграла).
2. Если гладкая кривая Г состоит из дуг Г1 и Г2, то для любой непрерывной на Г вектор-функции 
имеет место равенство:
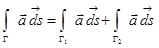
(аддитивность криволинейного интеграла).
3. Если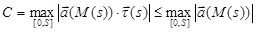 
, то
.
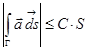Помимо этих свойств, криволинейный интеграл обладает свойством менять знак при изменении ориентации кривой.
4. Если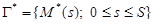 
– кривая с противоположной ориентацией, то
.
Действительно, в этом случае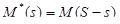 
,
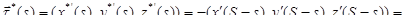
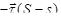, а потому
.
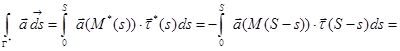
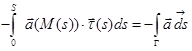Рассмотрим теперь ситуацию, когда гладкая кривая Г задается при помощи произвольного параметра t:
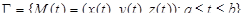. Функции x(t), y(t), z(t) непрерывны вместе с производными 
, 
, 
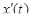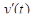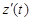на отрезке [a, b], причем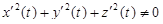 
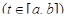. В таком случае переменная длина дуги s является строго возрастающей непрерывно дифференцируемой функцией параметра t. Но тогда обратная функция t(s) также является строго возрастающей и непрерывно дифференцируемой функцией на отрезке [0, S] (S – длина кривой Г), и можно перейти к такому представлению кривой, когда в качестве параметра берется переменная длина дуги S:
.
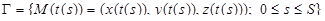Для единичного касательного вектора будем иметь:
.
Пусть на кривой Г задана вектор-функция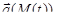 
, непрерывно зависящая от параметра 
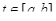. Тогда вектор-функция 
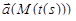непрерывна по 
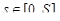. По формуле замены пере-менной в определенном интеграле получим:
|
|
|
Тем самым получена формула для вычисления криволинейного интеграла в случае произвольного параметра на гладкой кривой:
.
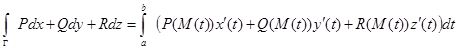Вид интеграла в правой части не зависит от того, какой параметр берется на кривой. Если кривая Г – кусочно-гладкая, то ее можно представить в виде объединения гладких частей: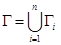 
(все Гi – гладкие кривые, конец Гi–1 совпадает с началом Гi i = 2,…,n). Криволинейный интеграл от непрерывной вектор-функции 
по кусочно-гладкой кривой Г определяется как сумма интегралов по гладким частям:
.
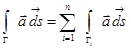Замечание. Криволинейный интеграл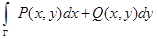 
от двумерной вектор-функции 
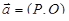вдоль плоской кривой 
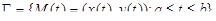можно рассматривать как частный случай интеграла
,
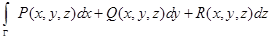считая 
, 
, 
, 
.
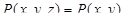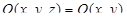Механический смысл криволинейного интеграла от вектор-функции 
по кривой Г: 
равен работе переменной силы 
вдоль дуги кривой Г.
Пример. Вычислить работу силы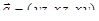 
вдоль дуги винтовой линии Г x = cos t,
y = sin t, z = t, (0 £ t £ 2p).
Решение. Имеем:
.
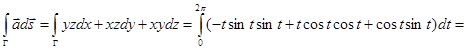
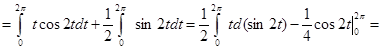
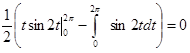Формула Грина
Теорема 3. Если D – замкнутая плоская область, ограниченная кусочно-гладким контуром Г; функции P(x, y) и Q(x, y) непрерывны в D вместе со своими частными производным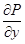и 
и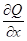 
, то имеет место формула Грина:
|
|
|
,
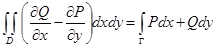где в криволинейном интеграле справа граница Г обходится против часовой стрелки.
Формулу Грина можно использовать в обеих направлениях: с одной стороны, она позволяет свести вычисление криволинейного интеграла к вычислению двойного; с другой стороны, часто оказывается проще вычислить соответствующий криволинейный интеграл. В качестве примера рассмотрим формулу для площади плоской области. Для этого в формуле Грина положим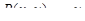 
, 
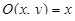. Тогда будем иметь 
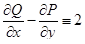и
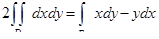, или
.
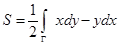Итак, для нахождения площади плоской области следует вычислить криволинейный интеграл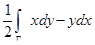 
вдоль ориентированной против часовой стрелки границы Г.
Пример. Вычислить площадь фигуры, ограниченной эллипсом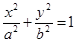 
.
Решение. Воспользовавшись параметрическим представлением эллипса x = a cos t, y = b sin t, (0 £ t £ 2p) будем иметь:
.
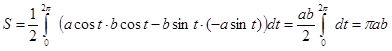Дата добавления: 2018-09-23; просмотров: 307; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!