Предел, непрерывность, частные производные для функции нескольких переменных
Предел, непрерывность, частные производные для функции нескольких переменных опреде-ляются так же, как в случае двух переменных. Так, если u = f(x, y, z), то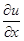 
– производная, получающаяся при дифференцировании u по x, когда y и z считаются постоянными. Правила дифференцирования сложной функции тоже сохраняются.
Касательная прямая и нормаль к графику неявной функции
Пусть линия L задана уравнением f(x, y) = 0, не решенным относительно y. Найдем y¢ для неявной функции, определяемой этим уравнением. Дифференцируем по x, помня, что y есть функция от x:
; 
.
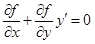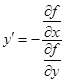Уравнение касательной прямой в точке 
:
; 
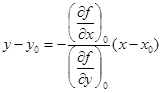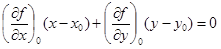. (1.32)
Уравнение нормали:
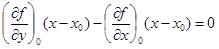. (1.32')
Касательная плоскость и нормаль к поверхности, заданной неявным уравнением
Пусть уравнение поверхности будет f(x, y, z) = 0. Это уравнение определяет “столбик” z как неявную функцию от двух переменных x и y. Рассуждая как в предыдущем подразделе и отправляясь от уравнения касательной плоскости (1.14), найдем, что теперь касательная плоскость в точке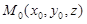 
будет иметь уравнение:
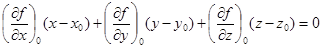. (1.33)
Прямая, проведенная через точку M0 нашей поверхности перпендикулярно к касательной плоскости, называется нормалью к поверхности и имеет уравнение:
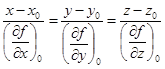. (1.33')
Скалярное поле
|
|
|
Пусть D – некоторая область на плоскости или в пространстве. Если в ней задана функция
u = f(x, y) (D – на плоскости) или u = f(x, y, z) (D – пространственная область), то говорят еще, что в области D задано (наведено) скалярное поле. Например, u – температура в точках D (поле температур) или u – давление жидкости или газа в точках сосуда D (поле давлений). При такой трактовке линии уровня (плоский случай) или поверхности уровня (пространственное поле) функции u приобретают важный физический смысл. Для поля температур – это изотермы: линии (поверхности) одинаковой температуры, для поля давлений – изобары: линии (поверхности), на которых давление одинаково.
Производная по направлению
При изучении скалярного поля бывает важно иметь информацию о скорости изменения величины поля в том или ином направлении. Это приводит к понятию производной по направлению. Рассмотрим случай плоского поля (рис. 10).
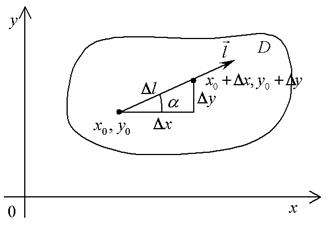
Рис. 10
В области D задано поле величины u = f(x, y). Надо определить в данной точке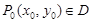 
скорость изменения поля в заданном направлении 
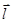. Направление характеризуется вектором, составляющим угол a с осью Ox. Переместимся из точки (x0, y0) в направлении вектора 
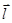на величину Dl. Попадаем в точку 
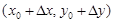, где (см. рис.10) 
, 
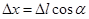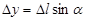. Изменение функции u на пути Dl есть
|
|
|
[считаем функцию дифференцируемой, 
и 
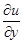вычислены в начальной точке (x0, y0)].
Средняя скорость изменения u на пути Dl будет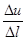 
, а скорость в точке P0:
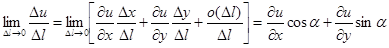. (1.34)
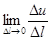называется производной по направлению l и определяет скорость измененияфункции в этом направлении. Эта производная обозначается 
:
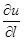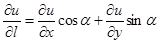. (1.35)
Теперь мы можем трактовать частные производные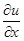 
, 
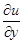как производные по направ-лениям (положительным!) осей Ox и Oy. Производная в отрицательном направлении оси Ox, например, будет – ( 
).
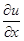В случае пространственного поля u = f(x, y, z) вектор направления 
характеризуется
углами a, b, g, составленными им с осями координат. Рассуждая как выше, мы найдем:
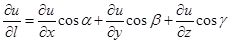. (1.36)
Градиент скалярного поля
В каждой точке (x, y) области D, где задана функция u = f(x, y) (скалярное поле), определим вектор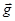 
, координатами которого будут частные производные u, вычисленные в этой точке:
, 
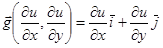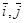– орты осей. (1.37)
Вектор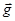 
называется градиентом функции u. В каждой точке D значение градиента, вообще говоря, свое и мы получаем в D поле новой природы – векторное поле градиента функции u (рис. 11).
|
|
|
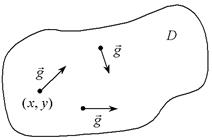
Рис. 11
Градиент обладает рядом полезных свойств:
1) производная по направлению есть проекция градиента на это направление. (Конечно, речь идет о производной и градиенте для одной и той же точки.) Будем считать, что вектор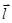 
, задающий направление, имеет длину единица. Тогда 
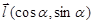. Проекция 
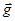на направление 
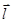равна скалярному произведению этих векторов; 
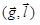– скалярное произведение.
.
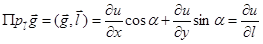(Скалярное произведение векторов есть сумма произведений их одноименных координат);
2) в данной точке наибольшая скорость изменения функции u происходит в направлении ее градиента (рис. 12). Эта наибольшая скорость равна модулю градиента: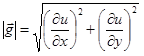 
. Свойство следует из того, что самая большая проекция вектора 
получится, когда проектирование осуществляется на направление самого (катет всегда меньше гипотенузы);
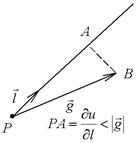
Рис. 12
3) градиент, построенный в точке P, перпендикулярен касательной к линии уровня функции u, проходящей через эту точку.
Уравнение линии уровня функции u = f(x, y) будет f(x, y) = C [если у точки P координаты (x0, y0), то ее принадлежность линии уровня означает, что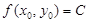 
]. Найдем угловой коэффициент касательной к линии. Дифференцируем по x неявно заданную уравнением 
функцию y = y(x):
|
|
|
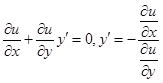– это угловой коэффициент к касательной. Угловой коэффициент прямой, идущей по градиенту 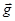, будет
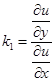и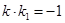 
, а это – условие перпендикулярности прямых.
Таким образом, градиент направлен по нормали к линии уровня (рис. 13).
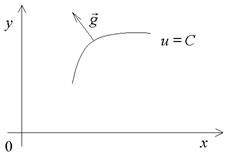
Рис. 13
В случае пространственного поля u = f(x, y, z) градиент – это вектор:
, 
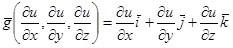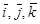– орты осей. (1.38)
Свойства 1) и 2) сохраняются, а свойство 3) формулируется так: градиент направлен по нормали к поверхности уровня.
2. Дополнительные вопросы приложений
дифференциального исчисления к геометрии
Плоские кривые. Кривизна
Дифференциал длины дуги
Рассмотрим график L дифференцируемой функции y = f(x). Положение точки на кривой L будем задавать, указывая длину S дуги кривой от некоторой начальной точки A до взятой точки.
На рис. 14 взята точка M0, S – длина дуги от A до M0 (S называют дуговой координатой точки M0). Дадим независимой переменной приращение Dx. На графике возникнет новая точка M, а дуга S изменится на DS – приращение длины дуги. Поскольку функция у нас дифференцируемая, то можно доказать, что
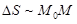при 
– хорда). (2.1)
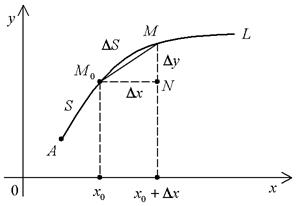
Рис. 14
Из рис. 14 видно, что 
. Мы можем теперь вычислить производную от дуги S по независимой переменной x (в точке x0):
( 
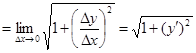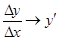при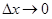 
). (2.2)
Отсюда дифференциал длины дуги
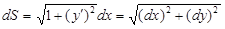, так как 
. (2.3)
Из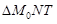 
(рис. 15) видим:
.
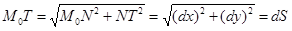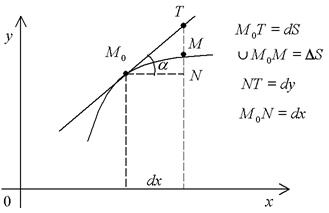
Рис. 15
Таким образом, dS – отрезок касательной прямой. Поскольку дифференциал эквивалентен приращению при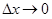 
, то из рис. 15 следует
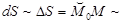хорде M0M.
Если кривая L задана параметрическими уравнениями
, 
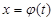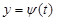, (2.4)
то из (3) получим такую формулу для dS:
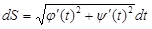. (2.5)
Кривизна плоской линии
Поскольку в бесконечно малых участках кривая очень хорошо заменяется отрезками своих касательных прямых, за меру искривленности того или иного участка кривой можно было бы принять угол, на который повернулась касательная прямая на этом участке. Рассмотрим рис. 16.
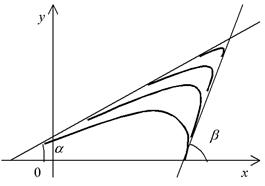
Рис. 16
Каждая из изображенных там дуг в начальной своей точке касается прямой, наклоненной под углом a, а в конечной – прямой с углом наклона b. Таким образом, касательная для каждой из этих дуг поворачивается на угол b – a. И все-таки ощущается, что большие дуги на этом рисунке более пологие, а малые поворачиваются быстрее, более изогнуты. В чем дело? Для больших дуг этот поворот происходит на участке, имеющем большую длину, чем для малых. Один и тот же поворот вызван перемещением на разную длину для разных кривых. Поэтому, чтобы получить более правильное представление об изогнутости кривой, угол поворота касательной соотносят с длиной соответствующего участка кривой.
На рис. 17 касательная на участке M0M длины DS повернулась на угол Da. Число
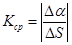(2.6)
принимается за среднюю кривизну этого участка, а кривизна в какой-то точке M0 это:
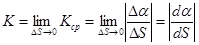. (2.7)
Обозначение модуля стоит потому, что в этом вопросе важна именно абсолютная величина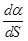 
, а не знак. Вычислим кривизну. Мы помним, что 
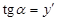. Поэтому 
,
.
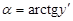Мы воспользовались (2.2) и формулой производной для арктангенса. Итак,
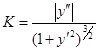. (2.8)
Для параметрически заданной кривой формула (2.8) пересчитывается следующим образом:
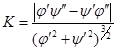. (2.9)
Из (2.7) следует, что K есть скорость изменения угла наклонакасательной относительно изменения длины кривой.
Для окружности радиуса R средняя кривизна любой дуги (независимо от ее длины)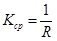 
; но тогда и кривизна K в любой точке, поскольку 
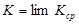, будет такая же: 
.
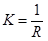Действительно (рис. 18), возьмем дугу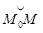 
. При ее обходе радиус повернется на угол a,
а длина ее будет R a. Касательная при обходе дуги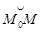 
также повернется на угол a (в силу перпендикулярности касательной к радиусу получаются углы с попарно перпендикулярными сторонами). Значит, 
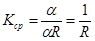и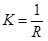 
.
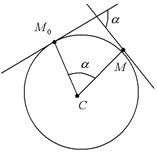
Рис. 18
Прямая линия представляется уравнением y = ax + b. Поэтому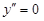 
и согласно (2.8) в любой точке K = 0. Для любой кривой в точках, где 
, будет K = 0. В частности, так будет в точках перегиба кривой. В этих точках кривая является “более прямой”, чем в остальных.
Дата добавления: 2018-09-23; просмотров: 346; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!