Приращения независимых переменных и приращение функции

 

Пусть f(x, y) задана в области D и P₀(x₀, y₀) – внутренняя точка области D. Дадим аргументам x и y приращения Dx и Dy – произвольные, такие, однако, чтобы точка 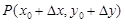 еще не выпала из D. Тогда

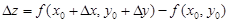                                          (1.4)

– полное приращение функции.

Геометрически Dz дает изменение аппликаты точки на поверхности z = f(x, y) при переходе от позиции 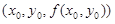 к позиции 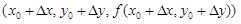, т.е. разность длин “столбиков”, поставленных соответственно в точках  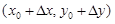и 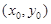. Условие непрерывности f(x, y) в точке (x₀, y₀) можно записать и так:

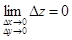.                                                            (1.5)

Если бы мы дали приращение Dx только переменному x или только приращение Dy переменному y, то возникли бы частные приращения функции:

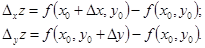                                            (1.6)

Эти приращения – частные (по x и по y соответственно); теперь оправдано и название “полное” для (1.4).

 

 

Дифференциальное исчисление функций двух переменных

Частные производные

Частными производными в точке (x₀, y₀) по x и y называются соответственно

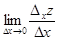 и 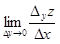.                                                      (1.7)

(Конечно, если эти пределы существуют.) Обозначаются они

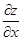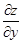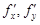,  или , или , или 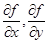                                          (1.8)

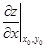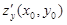и, если необходимо, показывается точка x₀, y₀ где вычислены частные производные:  или , или 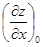 – например. Символы  (с круглыми ¶!) – не настоящие дроби в отличие от 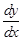, а лишь стилизованные обозначения пределов.

Чтобы вычислить частную производную по какому-то из переменных, надо действовать по обычным правилам дифференцирования, считая другое переменное неизменным, постоянным.

Пример 1. ;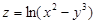

.

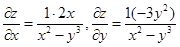Пример 2. ;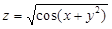

.

 

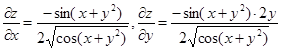Геометрический смысл частных производных

 

Проведем через точку (x₀, y₀) плоскость x = x₀, параллельную плоскости yOz. На рис. 6 это плоскость .

 

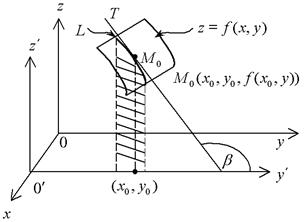
Рис. 6

 

Из поверхности z = f(x, y) эта плоскость вырежет кривую L. На L получится точка 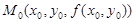 – конец “столбика”, восстановленного из (x₀, y₀). Проведем через M₀ касательную прямую к линии L (в плоскости сечения). Тангенс угла наклона b касательной к оси  (или, что то же, к оси Oy) и есть частная производная (по y) (рис. 6):

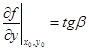.                                                            (1.9)

Это вытекает из геометрического смысла обычной производной. Аналогичным образом истолковывается . Касательная M₀T задается в пространстве системой двух уравнений первой степени:

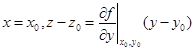.                                            (1.10)

Совершенно аналогичным образом, если провести сечение плоскостью y = y₀, то образуется касательная прямая в этой плоскости с уравнениями

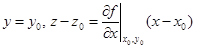.                                           (1.10’)

 

 

1.2.3. Касательная плоскость к поверхности z = f ( x , y )

 

Две касательные прямые, построенные в разделе 1.2.2, определяют плоскость. Эта плоскость называется касательной плоскостью к поверхности в точке M₀. Поскольку она проходит через точку 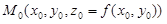, ее уравнение можно записать так:

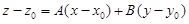.                                            (1.11)

(Проверьте, что координаты удовлетворяют (1.11).)

В сечении этой плоскости плоскостью x = x₀ образуется построенная нами касательная
прямая M₀T, для которой (см. 1.10)

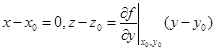.                                           (1.12)

Но из (1.11) следует, что

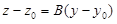.                                                         (1.13)

Сравнивая (1.12) и (1.13), видим, что 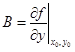; точно так же находится и 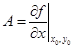. Подставляя все это в (1.11), получаем:

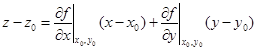                                      (1.14)

– уравнение касательной плоскости.

 

 

---

Дата добавления: 2018-09-23; просмотров: 304; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!