Дифференциал переменной длины дуги
Пусть дуга AB задана уравнением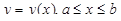 
, где функция y(x) непрерывно дифферен-цируема на отрезке [a, b]. Будем рассматривать на этой дуге переменную точку C с абсциссой x. Тогда длина дуги AC будет функцией s(x) переменной x:
.
(Здесь мы воспользовались тем, что определенный интеграл на отрезке [a, x] не зависит от того, какой буквой обозначается переменная интегрирования.) Функция s(x), как интеграл с переменным верхним пределом, дифференцируема и ее производная и дифференциал, соответст-венно, равны:
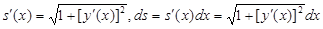. (3.9)
Аналогично для дуги, заданной параметрическими уравнениями x = x(t), y = y(t), 
,
где x(t), y(t) – непрерывно дифференцируемые на отрезке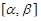 
функции, длина s(t) переменной дуги будет функцией t, определяемой равенством
и ее дифференциал будет равен
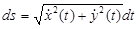. (3.10)
В случае дуги с уравнением в полярных координатах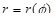 
имеем аналогично 
.
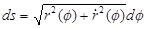Для пространственной кривой x = x(t), y = y(t), z = z(t), где x(t), y(t), z(t) - непрерывно дифференцируемые функции на отрезке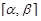 
, имеем
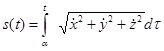. (3.12)
Так как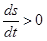 
, то s(t) монотонна и имеет обратную функцию t = t(s). Следовательно, длина дуги может служить параметром и уравнения кривой тогда примут вид
, 
, 
, 
,
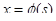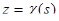где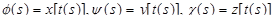 
. Эти уравнения называются натуральными уравнениями кривой.
Площадь поверхности вращения
Пусть поверхность s образована вращением вокруг оси x дуги AB, заданной уравнением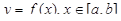 
, где f(x) – неотрицательная непрерывно дифференцируемая на отрезке [a, b] функция. Поставим задачу: вычислить площадь этой поверхности.
За площадь S поверхности вращения s принимают предел площадей поверхностей, образованных вращением вокруг оси x вписанных в дугу AB ломаных, при неограниченном увеличении числа звеньев ломаной и стремлении к нулю наибольшей из длин ее звеньев. Покажем, что
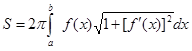– формула площади поверхности вращения. (3.13)
Разобьем отрезок [a, b] на n частей точками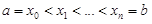 
и впишем в дугу AB ломаную с вершинами 
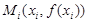, i = 0, 1,…, n. Площадь поверхности, образованной враще-нием этой ломаной вокруг оси x, есть сумма площадей боковых поверхностей усеченных конусов. Площадь боковой поверхности усеченного конуса, полученной при вращении вокруг оси x
звена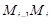 
(рис. 18), равна
,
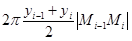где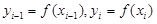 
и 
– длина звена 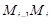. Так как функция f(x) дифференци-руема, то (см. вывод формулы (3.6) в п. 3 этой главы)
,
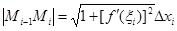где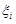 
– некоторая точка отрезка 
, а так как функция f(x) непрерывна на отрезке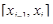 
, то существует точка 
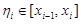такая, что 
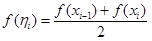. Тогда площадь боковой поверхности рассматриваемого усеченного конуса равна 
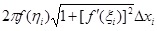, а площадь поверхности, образованной вращением вокруг оси x всей ломаной, равна
.
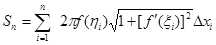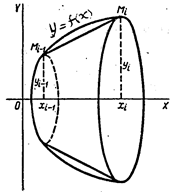
Рис. 18
Наряду с этой суммой рассмотрим интегральную сумму
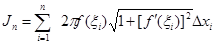
для интеграла в формуле (3.13) и перейдем к пределу при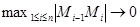 
. Заметим, что
при этом будет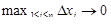 
. Так как f(x) – непрерывно дифференцируема, то функция 
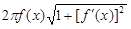непрерывна на отрезке [a, b] и
.
Можно доказать, что для непрерывно дифференцируемой на отрезке [a, b] функции f(x) суммы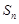 
и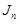 
будут при этом иметь общий предел, что доказывает равенство (3.13).
Пример. Вычислить площадь части поверхности параболоида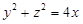 
, отсеченной плоскостью x = 1.
Решение. Данная поверхность является поверхностью, образованной вращением вокруг оси x дуги параболы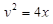 
, 
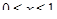. Тогда 
, 
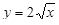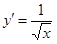и по формуле (3.13) получаем
.
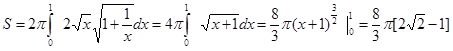Получим теперь формулы для площади поверхности вращения в случаях, когда дуга AB задана параметрическими уравнениями или уравнением в полярных координатах. Заметим, что согласно равенству (3.9) 
и формула (3.13) может быть записана в виде
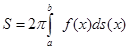. (3.14)
Тогда в случае задания дуги AB параметрическими уравнениями x = x(t), y = y(t), где функции x(t), y(t) непрерывно дифференцируемы на отрезке 
– монотонна и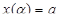 
, 
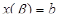, в результате замены переменной x = x(t) в интеграле в равенстве (3.14) с учетом равенства (3.10) получаем 
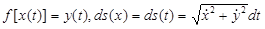, что приводит к интегралу
.
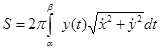Аналогично в случае, когда дуга AB задана уравнением в полярных координатах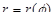 
,
где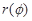 
– непрерывно дифференцируемая на отрезке [a, b] функция, замена переменной 
дает 
, 
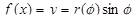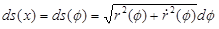и
.
Дата добавления: 2018-09-23; просмотров: 455; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!