Расчет дополнительных параметров условий стрельбы

Дополнительными параметрами условий стрельбы являются  скорость сближения с целью 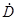 и проекции абсолютной  угловой скорости визирной линии 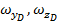.   В  курсовой  работе эти  параметры необходимо вычислять. Формулы для вычисления дополнительных параметров  могут быть получены из уравнения (2.14) для вектора скорости цели в случае ее определения синхронным способом.

 

(3.1)

.

 

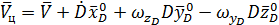Векторы 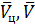записываются через единичные векторы системы ''D'' в следующем виде:

	(3.2)

,

	(3.3)

,

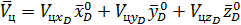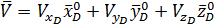где 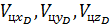- проекции скорости цели на оси системы координат “D”,  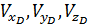   - проекции скорости самолета на оси системы координат “D ”.

 

Решая совместно (3.1),(3.2),(3.3),получим

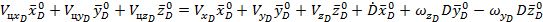(3.4) 4)

, (3.4)

или

(3.5))

.

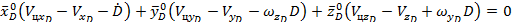Умножив скалярно уравнение (3.5) последовательно на орты осей системы координат “D”, получим следующие зависимости для определения искомых параметров

	(3.6)

,

	(3.7)

,

(3.8)

.

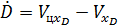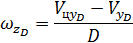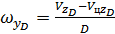Для определения проекций вектора 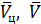 поступаем следующим образом. Введем систему координат 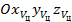, связанную с вектором воздушной скорости цели 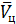. Система координат '' 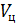'' получается путем поворота базовой системы координат на углы 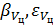. Тогда проекции вектора  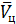на оси системы координат “D” могут быт определены путем перемножения следующих матриц преобразования  координат

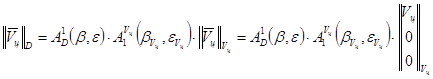.               (3.9)

 

где V_ц – заданное значение скорости цели; 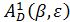- матрица перехода от системы '' 1'' к системе ''D'', определяемая углами β и ε; 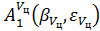- матрица перехода от системы '' 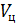'' к системе ''1'', определяемая углами .

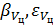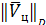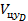Верхняя строка полученной матрицы  будет равна , средняя строка - , нижняя строка - .

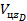Так как для пятой цели были сделаны допущения, что 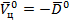, то формула (3.9) примет вид

.

(3.10)

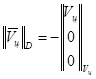Проекции вектора 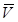 на оси системы ''D'' могут быть определены из произведения следующих  матриц  

(3.11)

,

 

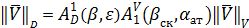где 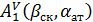- матрица перехода от системы '' 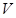'' к системе ''1'', определяемая углами атаки и скольжения.

Так как для расчета дополнительных параметров можно сделать допущения 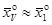(из-за малости углов атаки и скольжения), то

(3.12)

.

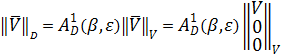В качестве примера приведем результат перемножения матриц в формуле (3.12).

(3.13)

 

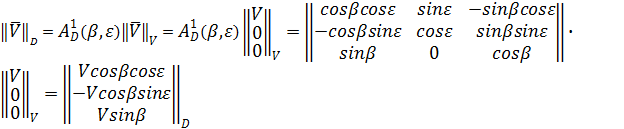
В расчетных формулах (2.18) – (2.20), определяющих параметры   Δβ и Δε и D_у , также имеются проекции ускорения цели 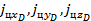 на оси лучевой системы координат “D”. Эти проекции в прицельной системе должны вычисляться по формулам (2.26) в зависимости от измеряемых и вычисляемых параметров .

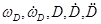В курсовой работе проекции ускорений вычисляются  в зависимости от заданных параметров условий стрельбы, точнее, в зависимости от заданной величины ускорения цели и ориентации вектора 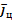 в системе “D”.

Введем систему координат 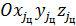, связанную с вектором ускорения цели 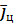, которая получается путем поворота базовой системы координат на углы 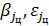. Тогда проекции ускорения цели  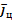в системе “D” могут быть определены путем перемножения следующих матриц преобразования координат вектора :

(3.14)

,

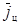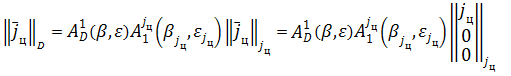где 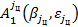 - транспортированная матрица перехода от системы координат ''1'' к системе координат '' 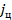'',определяемая углами .

Для цели №2 это ускорение задано, для цели №3 и цели №4 ускорение цели необходимо вычислять по формуле (1.1).

Для цели №5, выполняющей атаку бомбардировщика, проекции ускорения цели на оси системы координат ''D'' определяются по формулам

 

(3.15)

       где 

 

(3.16)

,

,

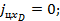
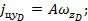
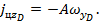
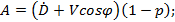
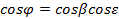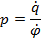где q – угол упреждения для самолета противника,

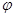              - угол упреждения для обороняющегося бомбардировщика.

Для самолета противника угол упреждения определяется по формуле

 

(3.17)

,

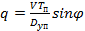где V – скорость бомбардировщика; T_п – время полета снаряда противника; D_уп – упрежденная дальность, определяющая фактическое положение снаряда противника.

(3.18)

Полагая  , получим производную от равенства (3.17) в виде

.

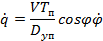С учетом полученной формулы

(3.19)

.

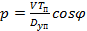Так как угол 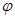, под которым может вести стрельбу противник, близок к 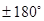(стрельба в заднюю полусферу), то для реального диапазона дальностей стрельбы и углов  величина 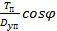 берется средним значением. Тогда

(3.20)

,

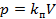где .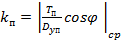                                                                          

Также для цели №5 необходимо пользоваться выражением для упрежденной дальности, равной упрежденной дальности при стрельбе из неподвижного оружия

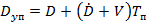                                                     .                                         (3.21)                                        

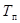Для определения времени полета снаряда противника  следует пользоваться известной формулой

,

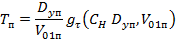где 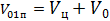, 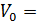1050 [м/с],  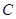= 1,8 [м²/кг] – абсолютная скорость снаряда противника, относительная начальная скорость и баллистический коэффициент снаряда американской пушки «Вулкан».

 

---

Дата добавления: 2018-09-22; просмотров: 269; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!