Линеаризация систем дифференциальных уравнений
Пусть поведение САР описывается системой дифференциальных уравнений
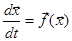(1)
Пусть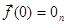 
, то есть начало координат является состоянием равновесия. Будем полагать, что функции fi(x1,…,xn), i=1,2,…,n имеют непрерывные частные производные в некоторой области 
. Разложим функции fi(x1,…,xn) в ряд Тейлора в окрестности точки (0,0,…,0):
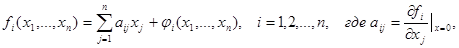(2)
а функции ji(x1,…,xn) содержат члены разложения порядка малости выше первого относительно переменных x1,…,xn и поэтому
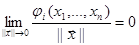. (3)
С учетом равенств (2) систему (1) можно переписать в виде
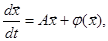
где A=[aij] – числовая матрица, а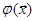 
– вектор-столбец, удовлетворяющий условию
.
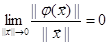Система линейных дифференциальных уравнений с постоянными коэффициентами
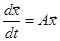
называется системой первого приближения для системы уравнений (1).
Функцию fi(x1,…,xn) можно получить в другом виде, не только разложением в ряд Тейлора. Существенно при этом, чтобы нелинейные члены ji(x1,…,xn) удовлетворяли условию (3).
Теорема Ляпунова об устойчивости по первому приближению гласит, что тривиальное решение системы
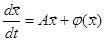
асимптотически устойчиво по Ляпунову, если все корни характеристического уравнения матрицы A этой системы имеют отрицательные вещественные части, то есть Re li<0, i=1,2,…,n.
Согласно теореме Ляпунова о неустойчивости по первому приближению, если среди корней характеристического уравнения матрицы A имеется хотя бы один корень с положительной вещественной частью, то тривиальное решение данной системы неустойчиво.
|
|
|
В том случае, когда среди корней характеристического уравнения имеются нулевые или чисто мнимые корни, нельзя судить об устойчивости тривиального решения данной системы по уравнениям первого приближения. В этом случае, называемом критическим, устойчивость или неустойчивость тривиального решения зависит от нелинейной части 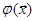. Путем соответствующего выбора 
можно сделать решение либо устойчивым, либо неустойчивым.
Пример 1: исследовать устойчивость тривиального решения системы уравнений
.
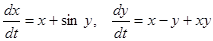Система первого приближения для этой системы имеет вид
.
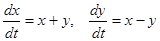Характеристическое уравнение
.
Его корни: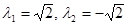 
. Первый корень лежит в правой полуплоскости. Значит, решение исходной системы неустойчиво.
Пример 2: исследовать устойчивость тривиального решения системы уравнений
.
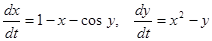Система первого приближения:
.
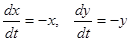Характеристическое уравнение:
.
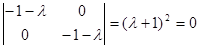Его корни: l1=l2=–1.
Оба корня лежат в левой полуплоскости, значит, тривиальное решение системы устойчиво.
Исследование устойчивости линейных систем с помощью второго метода Ляпунова.
Рассмотрим линейную стационарную систему:
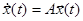(1)
Пусть положение равновесия этой системы будет находится в точке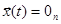 
. Будем искать функцию Ляпунова в виде:
|
|
|
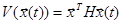
Рассмотрим производную этой функции в силу уравнения (1):
.
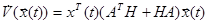Мы получили также квадратичную форму. Поэтому чтобы производная по времени от функции Ляпунова была отрицательно определенной, эта квадратичная форма должна быть отрицательно определенной. Обозначим:
.
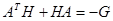Зададим матрицу G как некоторую положительно определенную матрицу. Тогда мы получим уравнение относительно матрицы H, называемое уравнением Ляпунова.
Если матрица H, найденная из этого уравнения, является положительно определенной матрицей, то система устойчива, в противном случае система неустойчива.
Дата добавления: 2018-09-22; просмотров: 291; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!