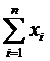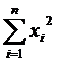Проверка гипотезы о равенстве средних (независимые выборки)
На практике встречаются случаи, когда средний результат одной серии наблюдений отличается от среднего результата другой серии наблюдений. Встает вопрос о значимости этих различий.
Случай известных дисперсий
Имеем две нормально распределенные независимые друг от друга случайные величины Х и Y с M(X) и M(Y).
Х: 

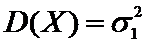 известна,
известна,
Y: 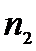
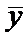
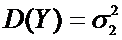 известна.
известна.
Требуется по выборочным средним и заданном 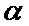 проверить значимость этого различия.
проверить значимость этого различия.
Решение. Выдвинем гипотезу
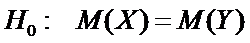 .
.
Альтернативная гипотеза может иметь вид:
а) 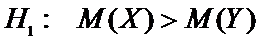 или
или  ,
,
б)  .
.
По выборочным значениям вычисляем
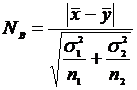 .
.
Случайная величина N (статистический критерий) имеет нормальное распределение N(0,1)
Определение 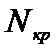 зависит от вида альтернативной гипотезы.
зависит от вида альтернативной гипотезы.
Случай а) Критическая область – односторонняя (правосторонняя или односторонняя.).
В дальнейшем – правосторонняя.
Критическая точка 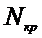 является решением уравнения:
является решением уравнения:

по таблице 2.
Случай б) Критическая область – двусторонняя и симметричная.
Правая критическая точка 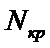 − решение уравнения:
− решение уравнения:
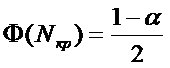 ,
,
по таблице 2.
|
|
|
Сравниваем 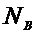 с критическим значением:
с критическим значением:
а) 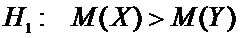 или
или 
- если 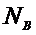
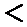

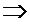 принимаем гипотезу
принимаем гипотезу 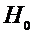 .
. 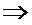 математические ожидания (генеральные средние) обоих распределений совпадают;
математические ожидания (генеральные средние) обоих распределений совпадают;
- если 


 отклоняем гипотезу
отклоняем гипотезу 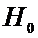 и принимаем гипотезу
и принимаем гипотезу  .
. 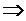 различие в вычисленных средних значениях значимо и математическое ожидание одного распределения действительно больше другого.
различие в вычисленных средних значениях значимо и математическое ожидание одного распределения действительно больше другого.
б) 
- если 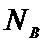
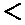
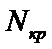
 принимаем гипотезу
принимаем гипотезу 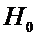
 математические ожидания (генеральные средние) обоих распределений совпадают;
математические ожидания (генеральные средние) обоих распределений совпадают;
- если 
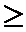
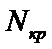
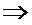 отклоняем гипотезу
отклоняем гипотезу  и принимаем гипотезу
и принимаем гипотезу 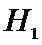
 различие в вычисленных средних значениях значимо, и математические ожидания распределений не совпадают.
различие в вычисленных средних значениях значимо, и математические ожидания распределений не совпадают.
Если объемы выборок большие и дисперсии неизвестны, то можно считать что
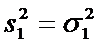 и
и  .
.
Проверка гипотезы о равенстве средних значений
(независимые выборки)
Случай неизвестных, но равных дисперсий
Условия задачи:
Х: 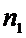
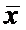
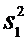 ,
,
Y: 
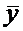
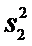 , причем
, причем  .
.
Требуется по выборочным средним и заданном уровне значимости 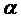 проверить гипотезу
проверить гипотезу
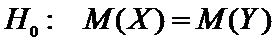 .
.
Схема решения при равенстве дисперсий:
(таблица)
Случайная величина T имеет t-распределение Стьюдента, симметричное относительно нуля.
|
|
|
Проверка гипотезы о равенстве средних двух нормальных совокупностей
Зависимые выборки)
Ранее при сравнении средних двух серий измерений предполагалось, что эти измерения проводятся независимо друг от друга.
Такое условие не выполняется, если следим за развитием болезни у одних и тех же больных.
Пусть, например, группа объектов подвергается какому-то воздействию. Измеряется некоторый признак до и после воздействия.
Требуется проверить влияние воздействия на данный признак.
Условия задачи:
Х: 
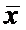
Y: 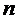
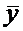 ,
,
Наблюдения сделаны у тех же объектов, т.е. выборки зависимы.
Рассмотрим случайную величину
D= Y –X: 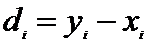 .
.
Тогда условие задачи сводится к проверке гипотезы
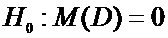
 .
.
Таблицы наблюдений
Если число наблюдений n небольшое, то результаты наблюдений 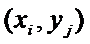 представляются в виде таблицы наблюдений
представляются в виде таблицы наблюдений

| 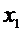
| 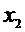
| . . . | 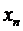
|
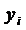
| 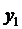
| 
| . . . | 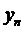
|
Оценками математических ожиданий являются выборочные средние значения
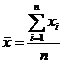
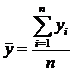 , (3)
, (3)
Несмещенные оценки дисперсий 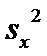 и
и  :
:
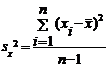
 (4)
(4)
|
|
|
Несмещенная оценка корреляционного момента называется эмпирический корреляционный момент:
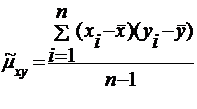 (5)
(5)
Оценка коэффициента корреляции:
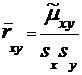 , (6)
, (6)
или
 (7)
(7)
при этом
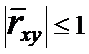 (8)
(8)
Расчетные формулы
Для вычисления числовых характеристик таблицу наблюдений удобно дополнить до следующей таблицы:
| № | 1 | 2 | n | суммы | |
| xi | x1 | x2 | … | xn |
|
| yi | y1 | y2 | … | yn |
|
| xi2 | x12 | x22 | … | xk2 |
|
| yi2 | y12 | y22 | … | yn2 |
|
| xiyi | x1y1 | x2y2 | … | xnyn |
|
Используя последний столбец таблицы, находим оценки числовых характеристик
а) математических ожиданий по формуле (3),
б) несмещенных оценок дисперсии
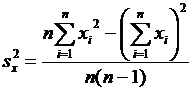 , (9)
, (9)
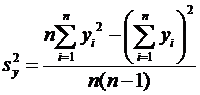 , (10)
, (10)
в) корреляционного момента:
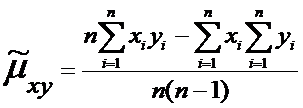 , (11)
, (11)
г) коэффициента корреляции:
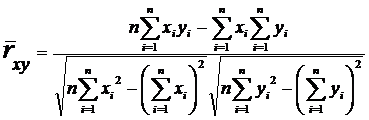 . (12)
. (12)
Дата добавления: 2018-08-06; просмотров: 241; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!