Принципы построения LQ регулятора
Рассмотрим базовую схемуLQрегулятора, изображенную на рисунке 1. Это упрощенная и идеализированная форма системы, моделью является электрическая печь. Температуру, внутри которой можно контролировать в данном месте – выходная переменнаяy(t).
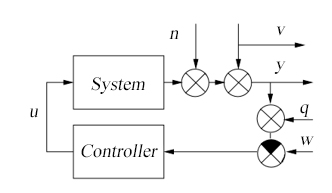
Рисунок 1 – Схема LQрегулятора
Температура зависит от энергии, которую обычно меняем, изменяя электрический ток и температуру в окружающей области. Таким образом, электрический ток является одновременно входной переменной системой u(t) и выходной переменной регулятора. Эффекты других переменных представлены помехами n(t). В этой модели идет изменение напряжения питания, которое также влияет на входную мощность и изменением окружающей температуры. Иногда более точное определение возмущения может быть уточнено. Влияние напряжения может быть определено с относительной точностью, если знать, как оно себя ведет, то его можно эффективно компенсировать. Этот тип помех назван «измеримым» и он представлен сигналом v(t)на диаграмме. Выходная переменная системы y(t), которая измеряется регулятором, для использования в переходном процессе, не всегда соответствует истинной физической переменной. Эта разница представлена сигналом q(t). Не учитывая этот сигнал, но предполагая, что дана точная измерительная система.
В разделе, посвященном свойствам LQ регуляторов, показано, как его эффекты могут ощущаться. Переменная w(t)на диаграмме представляет заданное значение. В конструкции регулятора необходимо выбрать критерий и процесс модели, использовать подходящую процедуру оптимизации. Поэтому выбор периода является важным фактором при проектировании LQрегулятора, при непрерывном процессе.
|
|
|
2.1 КритерииLQрегулятора
Целью управления является формирование типа входного сигнала u(k), который приводит к выходу системы вблизи заданного значения k
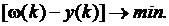
Это означает, что критерий, используемый для оценки качества регулятора, должен быть неотрицательной функцией всех переменных 
при тех значенияхk, которые используем в модели. Эти условия удовлетворяются квадратичным критерием
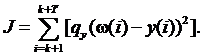
Оценивая качество регулятора, также учитываем задержку более крупного входного сигнала для улучшения качества переходного процесса. Это отражено в следующем критерии
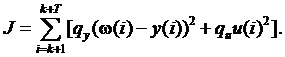
Где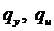 
,T – основные параметры критерия подберем таким образом, чтобы критерий представлял собой определенное оптимальное поведение регулятора. Ивключим опорный сигнал для выходной переменной системы регулятора, используя расширение квадратичного критерия, имеющий форму
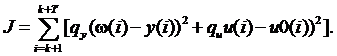
Это приводит к тому, что выходная переменная системы зависит от еще одного выбранного сигнала, и используем ее для сохранения полезных свойств регулятора.
|
|
|
2.2 МодельLQрегулятора
ПринципLQмоделисостоит в том, что она начинается с текущего времени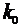 
и генерирует значения 
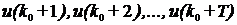, чтобы свезти будущую ошибку до минимума. Применим метод LQ на практике, для этого, определим будущее значение всех сигналов (переменных), встречающихся в критерии. В простейшем случае эта модель, используется для вычисления будущих значений выходной переменной системы y(k), и определяет поведение заданного значения в будущем.
Линейная модель, которая удовлетворяет минимизации квадратичного критерия, представляет собой линейную регрессию. Поскольку модель является хорошей с точки зрения идентификации параметров и может быть использована в синтезе, то наиболее часто используется в адаптивных регуляторах. Рассмотрим модель регрессии с измеряемой внешней помехой (преобразованная на выходной переменной системы), то есть регрессионную модель
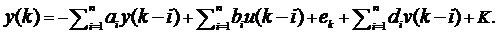
Имеется ввиду, что одно разностное уравнение (модель регрессии) может быть представлено несколькими передаточными функциями.
Аналогичная структура регулятора, изображенная на рисунке 2, представлена большим количеством передаточных функций.
|
|
|
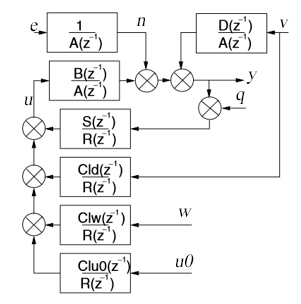
Рисунок 2 – Структура LQрегулятора
Минимизация критерия приведет к разностному уравнению для оптимального выходного сигнала u(k) в виде
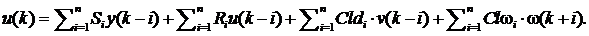
Полученный закон представляет собой обратную связь с выходной переменной системы и сигнал от индивидуальных измеряемых переменных. Из этого следует, что регулятор не работает с ошибкой, но независим от каждого отдельного сигнала. Если сравним свойства цикла, когда ошибка сначала вводится на вход регулятора, то цикл должен быть преобразован в структуру, изображенную на рисунке 3.
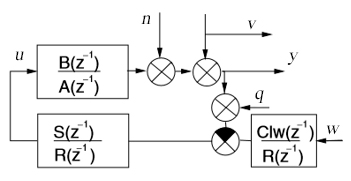
Рисунок 3 – Преобразованная структураLQ регулятора
Структура регулятора тесно связана со структурной моделью. Все передаточные функции, созданные на базе модели, используются в регуляторе. Если, используется только часть обратной связи, то можно ожидать значительного ухудшения поведения модели [5].
2.3 Оптимизационный подход
Стандартный метод минимизации квадратичного критерия для LQрегулятора выводится из состояния системы. Формирование пространства состояний позволяет использовать динамичное программирование, чтобы процесс минимизации выполнялся от конца интервала до начала. В модели линейного состояния пространства поэтапная минимизация приводит к эволюции матрицы квадратичной формы. Выражены в виде уравнения, известного, как дискретное уравнение Риккати.
|
|
|
Обычно линейно – квадратичный регулятор представлен в следующем виде:
y(k)=Cx(k)+Du(k).
Система определяется моделью дискретного пространства состояния. Где векторы x(k), y(k), u(k)представляют состояния, выходные и входные векторы и имеют размеры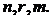 
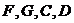– представляют собой матрицы состояния, ввода и вывода прямой структуры, а их размеры соответствуют значениям соответствующего вектора.
Цель состоит в том, чтобы найти последовательность законов управления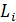 
, которые минимизируют критерий
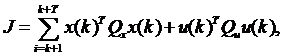
т.е. оптимизируютпереходные функции данного состояния x(0) к нулевому состоянию.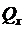 
и 
- являются матрицами содержащие критерии для входа и выхода, и где 
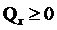и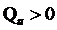 
являются допустимыми. Дискретное уравнение Риккати, которое представляет минимизацию, принимает форму
где индекс iследует считать итерацией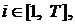 
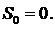Последовательность матриц 
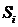определяет последовательность законов управления
и оптимальное управление рассчитывается из соотношения
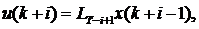
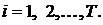
Все целые значения критерия на рассматриваемом интервале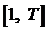 
задаются выражением
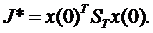
Используя соотношения уравнения Риккати,получится что
Значение T → ∞ имеет особое значение в теории управления. Фактически, когда говорят о линейно – квадратической задаче, почти всегда ссылаются на эту конкретную ситуацию. Она заключается в том, что минимизация этого критерия с бесконечным горизонтом приводит к стационарному закону управления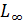 
, поэтому является неизменной. Она имеет устойчивое воздействие при стандартных условиях. Эти условия влияют на управляемость (способность к устойчивости) пары 
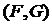и наблюдаемость (обнаруживаемость) пары 
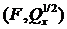. Этот закон управления получается из решения алгебраического уравнения Риккати. Если у него есть несколько решений, нужно выбрать положительно полуопределенное решение.
Это стационарное решение имеет ряд других интересных свойств, которые будут рассматриваться в другом разделе. Самым значительным из них является устойчивое воздействие не только для системы, для которой он предназначен, но и для систем, где амплитудные и фазовые частотные характеристики лежат на некотором расстоянии от номинального. Этот тип управления описывается как «надежный», с точки зрения устойчивости. Трудность состоит в том, что состояние должно быть доступным в целях управления. Доступ к состоянию технологических процессов редок, линейный квадратичный оптимальный контроль будет сформулирован при условии, что есть только доступ к системному выходу.Свойства двух типов управления могут сильно различаться, поскольку другая динамика входит в цикл, либо как передаточная функция динамического контроллера, если она полагается на функцию передачи системы, либо как динамика, используемого для восстановления неизмеримого состояния. Гарантия устойчивости и других критериев теряется, если к состоянию нельзя получить доступ.
Это состояние составлено из измеряемых сигналов, оно само не измеримо (чтобы получить эти переменные в момент времени k, предыдущие измеренные значения должны быть сохранены, возможно в сдвиговых регистрах, тем самым создавая наблюдение).Таким образом:
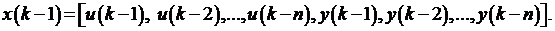
Здесь используем модель, состоящую из истинного ввода и вектора состояния
Матрица состояний этого типа модели состоит из параметров регрессионной модели; нулей и единиц. Используемое состояние не является минимальным. Однако покажем, что сложность расчета, используемая здесь, особенно в квадратной корневой форме, сопоставима со сложностью алгоритма, используемого для решения проблемы минимизации состояния.
Также используем формулировки состояния в линейной квадратичной задаче:
● альтернативный полиномиальный подход, обеспечивает решение только для бесконечного горизонта. Однако, в адаптивном подходе полезно представить устойчивое решение как пределы конечного горизонта, когда метод расчета не может найти устойчивого решения;
● формулировка состояния позволяет сформулировать грамотную стратегию и реализовать ее на практике;
● не минимальный подход состояния позволяет сформулировать стратегию с использованием зависящей от критерия переменной.
Разработанный алгоритм поэтапной минимизации квадратичного критерия, который не требует введения состояния и описания состояния.В отличие от классического подхода, когда состояние используется для выражения издержки, чтобы потерять критерий, используется квадратичную форма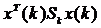 
, новый подход использует список тех переменных, которые способствуют потере.Этот список обновляется в ходе отдельных этапов минимизации. Обновление может быть гораздо более обобщенным, чем просто относящиеся толькок одному состоянию.
Дата добавления: 2018-08-06; просмотров: 385; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!