Однородные дифференциальные уравнения
1º. Понятие однородной функции
Определение 1. Функция f(x, y) называется однородной функцией степени m, если при любом t Î R имеет место тождество
f(tx, ty) = tmf(x, y). (1)
Примеры:
1) f(x, y) = x2 + 2xy
2) f(x, y) = x + 3xy
3) f(x, y) = 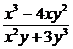
Докажем следующее свойство однородной функции:
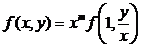 . (2)
. (2)
На самом деле в формулу (1) падставим 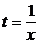 и получим
и получим
 ,
,
откуда получаем формулу (2).
2º. Однородные уравнения
Определение 2. Дифференциальное уравнение вида
M(x, y)dx + N(x, y)dy = 0 (3)
называется однородным относительно переменных x ,y, если M(x, y), N(x, y) однородные функции одной и той же степени.
Замечания. 1. Уравнения называют просто однородными. Но надо иметь в виду, что есть ещё дифференциальные уравнения, которые также называют однородными.
2. Уравнение вида
y¢ = f(x, y) (4)
называют однородным, если функция f(x, y) однородная степени 0. Это связано с тем, что уравнение (3) преобразуется в уравнение (4) с тем же свойством.
Чтобы проинтегрировать уравнение (3), используют замену 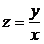 , где z — новая неизвестная функция от x.
, где z — новая неизвестная функция от x.
На практике используют равенство y = zx.
Находим дифференциал dy = zdx + xdz.
Используем свойство (2)
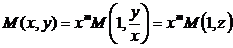 ,
,
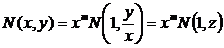 .
.
Подставим в (3)
xmM(1, z)dx + xmN(1, z)(zdx + xdz) = 0. (5)
|
|
|
Разделим на xm (!)
M(1, z)dx + N(1, z)(zdx + xdz) = 0,
(M(1, z) + zN(1, z))dx + xN(1, z) dz = 0.
Это уравнение с разделяющимися переменными.
Делим на x(M(1, z) + zN(1, z)) (!), получаем
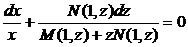 .
.
Если ввести обозначение 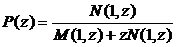 , получим
, получим
 , C ¹ 0, или
, C ¹ 0, или
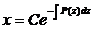
(!) Надо проверить, являются ли решениями уравнения функции x =0 и z = z0, где P(z0) = 0.
Потом возвращаемся к функции y.
Пример 4. 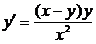 .
.
Однородное уравнение. Замена y = zx, dy = zdx + xdz.
Уравнение переводимим в дифференциальную форму
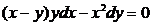 .
.
Подставляем
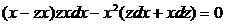 ,
,
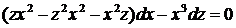 ,
,
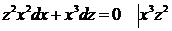 (!),
(!),
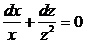 ,
,
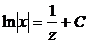 ,
,
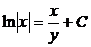
(!) Проверяем функции x = 0 и z = 0 Þ y = 0.
Функция x = 0 — не является решением.
Функция y = 0 — решение.
Вывод: 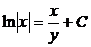 , y = 0.
, y = 0.
3º. Уравнения, которые сводятся к однородным
Рассмотрим уравнение вида
 . (6)
. (6)
Возможны два случая:
1). 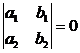 .
.
Строки определителя пропорциональны, поэтому существует число k такое, что
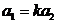 ,
, 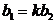 .
.
Имеем
 ,
,
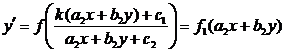 .
.
Гэта случай § 5, п. 3º.
Уравнение сводится к уравнению с разделяющимися переменными.
2). 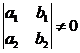 .
.
В этом случае алгебраичная система
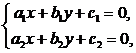
имеет единственное решение (x0, y0).
Делаем подстановку
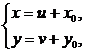
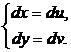
Соответственно,
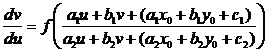 ,
,
 — однородное дифференциальное уравнение.
— однородное дифференциальное уравнение.
Пример 5.  .
.
|
|
|
Сначала вычислим определитель 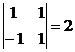 .
.
Решаем систему 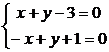 , x0 = 2, y0 = 1.
, x0 = 2, y0 = 1.
Делаем замену 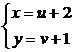 . Новое уравнение
. Новое уравнение  — однородное, переходим в дифференциальную форму
— однородное, переходим в дифференциальную форму
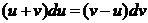 .
.
Замена 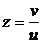 ,
, 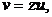
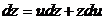 .
.
Подставляем
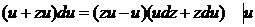
и преобразовываем
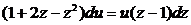 ,
,
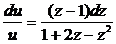 ,
,
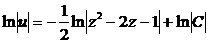 ,
,
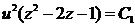 ,
,
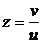 Þ
Þ 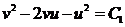 ,
,
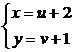 ,
,  Þ
Þ  , або
, або
 .
.
Однородные линейные дифференциальные уравнения первого порядка
1º. Основные понятия
Рассмотрим ОДУ первого порядка, разрешённое относительно производной
y¢ = f(x, y). (1)
Определение 1. Уравнение (1) называется линейным, если функция
f(x, y) линейная относительно y.
На практике эта задача означает, что функция имеет вид
f(x, y) = a(x)y + b(x).
Обычно линейное уравнение записвают в виде
y¢ + p(x)y = g(x), (2)
причём функции p(x) и g(x) считаются непрерывными на некотором промежутке I.
Определение 2. Уравнение вида
y¢ + p(x)y = 0, (3)
называется линейным однородным дифференциальным уравнением (ЛОДУ) первого порядка.
Если в уравнении (1) g(x) ¹ 0 тождественно, то уравнение называется неоднородным (ЛНДУ).
Линейное уравнение первого порядка всегда интегрируется в квадратурах.
|
|
|
2º. Общее решение линейного однородного уравнения
Рассмотрим ЛОДУ
y¢ + p(x)y = 0, (3)
где p(x)— непрерывная функция.
Это уравнение с разделяющимися переменными.
Преобразуем в дифференциальную форму
dy + p(x)ydx = 0 | y (!)
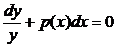 ,
,
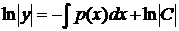 , C ¹ 0,
, C ¹ 0,
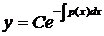 , C ¹ 0.
, C ¹ 0.
Функция y = 0 — решение, поэтому C = 0 включаем в общее решение.
Вывод. 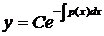 .
.
Пример. 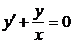
Записваем решение па формуле 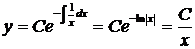 ,
, 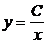 .
.
§ 9. Решение линейных неоднородных дифференциальных уравненияў первого порядка и уравнение Бернулли
1º. Структура общего решения неоднородного линейного уравнения
Рассмотрим ЛНДУ
y¢ + p(x)y = g(x), (1)
где g(x) ¹ 0 тождественно.
Пусть известно некоторое решение y1 ЛНДУ (1), т.е.
y1¢ + p(x)y1= g(x). (2)
Введём новую неизвестную функцию z по формуле z = y – y1.
Выражаем y = y1 + z и подставляем в (1)
(y1 + z)¢ + p(x)(y1 + z)= g(x),
y1¢ + z¢ + p(x)y1 + p(x)z = g(x),
y1¢ + p(x)y1 + z¢ + p(x)z = g(x),
Из (2) Þ g(x) + z¢ + p(x)z = g(x), или
z¢ + p(x)z = 0. (3)
|
|
|
Таким образом, z(x) — решение ЛОДУ (3).
Определение 1. Уравнение (3) называется линейным однородным уравнением, соответствующим неоднороднаму уравненю (1).
Фактически доказана
Теорема. Если y1 является решением ЛНДУ
y¢ + p(x)y = g(x), (1)
тогда общее решение этого уравнения имеет вид
y = y1 + z,
где z — общее решение соответствующего ЛОДУ
y¢ + p(x)y = 0. (3¢)
Замечание. Общее решение ЛОДУ первого порядка находится по формуле
 ,
,
поэтому общее решение ЛНДУ имеет вид
y = y1 + 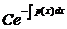 .
.
2º. Метод Бернулли
Частное решение y1 ЛНДУ первого порядка
y¢ + p(x)y = g(x), (1)
будем искать в виде произведения
y1(x) = u(x)v(x),
где v(x) — решение соответствующего однороднага дифференциальнага уравнения
v¢ + p(x)v = 0, (3¢¢)
а u(x) — новая неизвестная функция.
Подставляем y1(x) = u(x)v(x) в уравнение (1):
u¢v + uv¢ + p(x)uv = g(x),
u¢v + u(v¢ + p(x)v) = g(x),
из (3¢¢)
u¢v = g(x) Þ  .
.
Так как общее решение уравнения (3¢¢) имеет вид 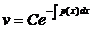 , выбираем конкретное значение C = 1 и получаем
, выбираем конкретное значение C = 1 и получаем
u¢ = 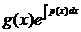 ,
,
откуда
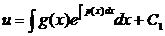 .
.
Выбираем C1 = 0, имеем
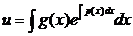 .
.
Тогда
y1 = uv = 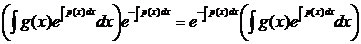 .
.
Этот способ нахождения частного решения ЛНДУ– метод Бернулли.
3º. Метод Лагранжа (метод вариации произвольной постоянной)
На практике для решения ЛНДУ (1) используют модифицикацию метода Бернулли, которая называется методом Лагранжа.
Общее решение соответствующего ЛОДУ (3) имеет вид
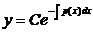 ,
,
и общее решение ЛНДУ (1) ищем в виде
 , (4)
, (4)
где C(x) — новая неизвестная функция.
Замечание. Фактически это снова произведение неизвестной функции и решения соответствующего ЛОДУ (метод Бернулли).
Метод вариации произвольной постоянной носит такое название, потому что произвольная постоянная в формуле решения соответствующего ЛОДУ стала неизвестной функцией (вариация произвольной постоянной).
Подставляем (4) в (1):
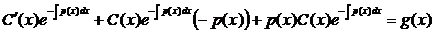 ,
,
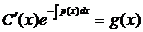 ,
,
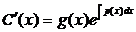 ,
,
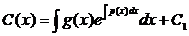 . (5)
. (5)
Подставляем (5) в (4) и получаем формулу общего решения ЛНДУ
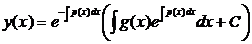 .
.
Пример 1.  .
.
Соответствующее ЛОДУ 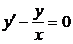 имеет решение
имеет решение 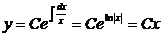 .
.
Общее решение ЛНДУ ищем в виде
y = C(x)x.
Подставляем в ЛНДУ
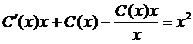 ,
,
C¢(x) = x, 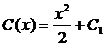
y = C(x)x =  =
= 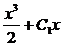 .
.
Вывод: 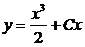 .
.
4º. Уравнение Бернулли
Определение 2. Уравнением Бернулли называется дифференциальное уравнение вида
y¢ + p(x)y = g(x)yα, (6)
где p(x) и g(x) непрерывные функции на промежутке I, α ¹ 0, α ¹ 1.
Если α = 0, это ЛНДУ первого порядка.
Если α = 1, это ЛОДУ первого порядка.
Уравнение Бернулли линейным не является. Оно сводится к ЛНДУ подстановкай z = y1 – α.
Можно также использовать метод Лагранжа (метод вариации произвольной постоянной).
Пример 2. 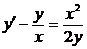 .
.
С помощью метода Лагранжа (α = –1).
Записываем и решаем соответствующее ЛОДУ
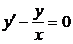 ,
, 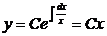 .
.
Решение уравнения Бернулли ищем в виде y = C(x)x.
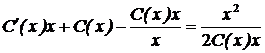 ,
,

2CdC = dx
C2(x) = x + C1 Þ 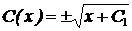
y = C(x)x =  ,
,
Вывод: y2 = x3 +x2C.
Дата добавления: 2018-08-06; просмотров: 215; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
