Физический и математический маятник.Энергия колебательной системы.Гармонический осциллятор.

Nbsp;

КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ И ЕГО ХАРАКТЕРИСТИКИ и уравнение.

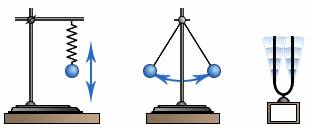
Рис. 1

Механические колебания – это движения, которое точно или приблизительно повторяются через одинаковые промежутки времени

. Различают

периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени.

Примерами механических колебаний могут служить движение шара на пружине, на нити, движение ножек звучащего камертона или молекул воздуха вблизи него (рис. 1)

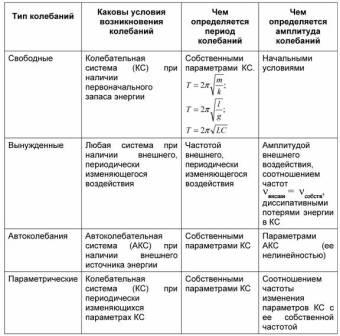
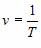Наиболее общими характеристиками колебаний являются следующие физические величины: амплитуда колебаний А наибольшее отклонение колеблющегося тела от положения равновесия (отклонение величины от ее среднего значения); период колебаний Т время, через которое движение тела полностью повторяется (повторяются все кинематические характеристики колебаний), т.е. совершается одно полное колебание; частота колебаний v – величина, показывающая число колебаний, совершаемых за 1 с. Вместо частоты v чаще пользуются понятием циклической частоты w. Циклическая частота w – это число колебаний, совершаемых за 2p секнд. Частота обратно пропорциональна периоду:

В СИ период Т выражается в секундах (c), частота v в герцах (Гц), циклическая частота w – в обратных секундах (с^–1).

Механические гармонические колебания.пружинный маятник.

Механические колебания Механическими колебаниями называются периодические (или почти периодические) изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальныая энергия и т. п.).

Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны. Примерами такого процесса являются звуковые волны в воздухе.

Механические колебания

Гармонические колебания

Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения. Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени.

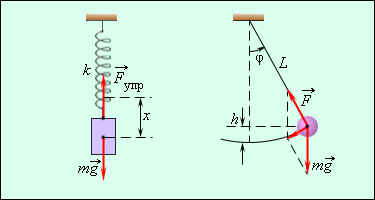
Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 2.1.1).

Рисунок 2.1.1. Механические колебательные системы

Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением

x = x_m cos (ωt + φ₀).

Здесь x – смещение тела от положения равновесия, x_m – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинусаφ = ωt + φ₀ называется фазой гармонического процесса. При t = 0 φ = φ₀, поэтому φ₀ называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебанийT. Физическая величина, обратная периоду колебаний, называется частотой колебаний:

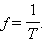
Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний fсвязана с циклической частотой ω и периодом колебаний T соотношениями:

При колебательном движении тела вдоль прямой линии (ось OX) вектор скорости направлен всегда вдоль этой прямой. Скорость υ = υ_x движения тела определяется выражением

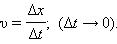
Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях:

следовательно, ускорение a равно производной функции υ (t) по времени t, или второй производной функции x (t). Вычисления дают:

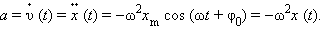
Знак минус в этом выражении означает, что ускорение a (t) всегда имеет знак, противоположный знаку смещения x (t), и, следовательно, по второму закону Ньютона сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия (x = 0).

ПРУЖИННЫЙ МАЯТНИКИ

Если колебания совершаются в системе за счет первоначально сообщенной энергии,

то они называются свободными. Примером таких систем являются модели

колеблющихся тел: математический маятник и пружинный.

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:

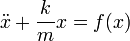, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:

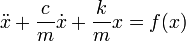
Физический и математический маятник.Энергия колебательной системы.Гармонический осциллятор.

Математический маятник– колеблющаяся материальная точка, подвешенная на невесомой и нерастяжимой нити. К этой модели ближе всего массивное тело (шар), размер (диаметр) которого много меньше длины нити. Если его отклонить от положения равновесия, увеличив при этом потенциальную энергию системы «шар–нить», то будут наблюдаться колебательные движения этой системы. Колебательное движение системы «шар–нить» будет наблюдаться и в том случае, если шару сообщить кинетическую энергию, т.е. заставить его двигаться.

Рассмотрев малые колебания математического маятника (рис. 4), при которых отклонение его от положения равновесия х можно получить выражение для периода его колебаний. ( в любой момент времени для этой системы выполняется закон сохранения механической энергии:

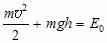
Выразив высоту h через координату x по оси 0Х (рис. 4, а) и учитывая, что при малых значениях х угол между нитью и вертикалью тоже мал, используем что для такого угла отклонения соотношение sin a » a » tg a.

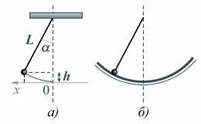Рис. 4

Следовательно,

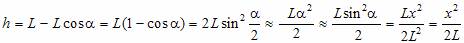
Из закона сохранения энергии получим

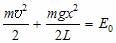
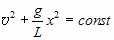
Поэтому можно утверждать (см. Уравнение гармонических колебаний), что малые колебания математического маятника происходят по гармоническому закону x = A sin (wt + j₀), где

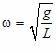
т.е. с периодом

Амплитуду и начальную фазу колебаний находят из начальных условий –начальной скорости и начальной координаты тела. Если, например, тело в моментвремени t находилось в начале координат и имело скорость ₀, то из уравнений = 0

x(0) = A sin j₀ = 0

(0) = Aw cos j₀ = ₀

находим

j₀ = 0, A = ₀/w.

ОСЦИЛЛЯТОР ГАРМОНИЧЕСКИЙ

система с одной степенью свободы, колебания к-рой описываются уравнением вида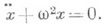

Фазовые траектории - окружности, период колебаний 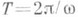не зависит от амплитуды. Потенциальная энергия О. г. квадратично зависит от х:

Примеры О. г.: малые колебания маятника, колебания материальной точки, закрепленной на пружине с постоянной жесткостью, простейший электрический колебательный контур. Термины "гармонический осциллятор" и "линейный осциллятор" часто употребляются как синонимы.

Колебания квантовомеханического линейного осциллятора описываются уравнением Шрёдингера

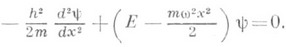
Здесь т - масса частицы. Е - ее энергия, h - постоянная Планка, w - частота. Квантовомеханический линейный осциллятор имеет дискретный спектр уровнен энергии 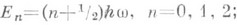соответствующие собственные функции выражаются через Эрмита функции.

Термин "осциллятор" употребляется но отношению к системам (механическим или физическим) с конечным числом степеней свободы, движение к-рых носит колебательныйхарактер (напр., многомерный линейный осциллятор - колебания материальной точки, находящейся в потенциальном поле сил с потенциалом, к-рый является положительно определенной квадратичной формой от координат, нелинейный осциллятор Ван дер Поля, см.Ван, дер Поля уравнение). По-видимому, не существует однозначного толкования термина "осциллятор" или даже "линейный осциллятор".

Физический маятник.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

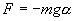
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

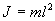. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

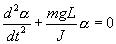
(7.10)

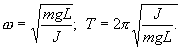
(7.11)

Решение этого уравнения

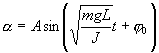
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. или

.
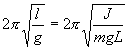Из этого соотношения определяем

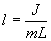
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

Дата добавления: 2018-08-06; просмотров: 1320; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!