Вывод расчетных формул метода Рунге – Кутты.

Пусть y (t) - решение дифференциального уравнения 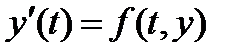, удовлетворяющее условию y (t_n)=y_n.

Запишем неравенство (19) в следующем виде:

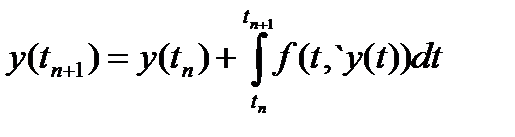(24)

Если бы входящий в это равенство интеграл можно было вычислить точно, то получилась бы простая формула, позволяющая последовательно вычислить значения решения в узлах сетки. Поскольку в действительности это невозможно, получим приближенную формулу, заменив интеграл квадратурной суммой.

На отрезке [t_n, t_n₊₁] введем m вспомогательных узлов

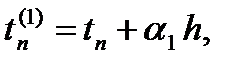
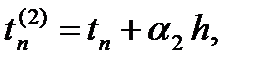
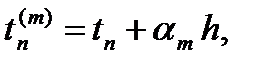
где 0 = a₁£a₂£ … £a_m£ 1. При этом заметим, что 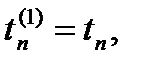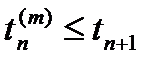. Заменяя входящий в равенство (24) интеграл квадратурной суммой с узлами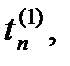 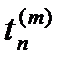, получаем приближенное равенство:

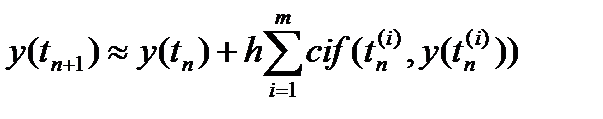(25)

Однако воспользоваться равенством (25) для вычисления y (t_n₊₁) нельзя, так как значения функции y в точках 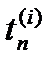для i = 2, 3, …, m неизвестны. Чтобы найти эти значения, запишем равенства

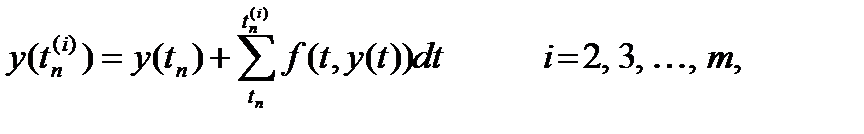(26)

аналогичны равенству (24).

Заменив для каждого i входящий в формулу (26) интеграл соответствующей ему квадратурной формулой с узлами 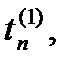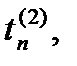…, придем к приближенным равенствам:

…

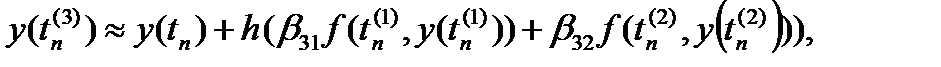
Эти равенства позволяют последовательно вычислять приближения к значениям .

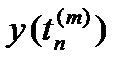Обозначим теперь через вспомогательные величины, имеющие смысл приближений к значениям пусть - приближение к значению углового коэффициента R в точке Тогда расчетные формулы примут вид:

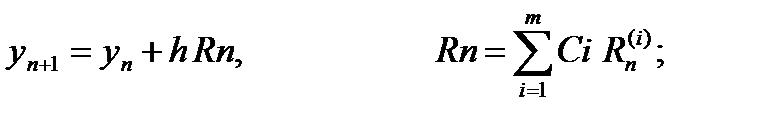
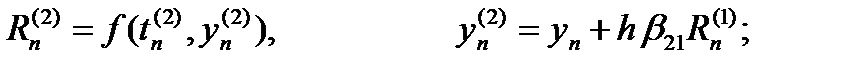
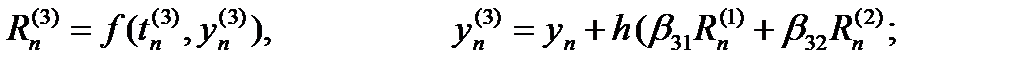
Часто из этих формул исключают вспомогательные величины и записывают формулы так:

…

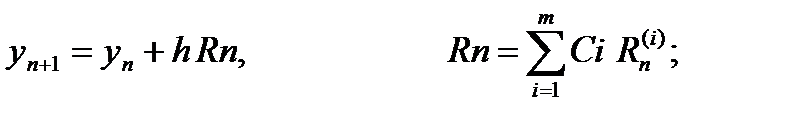
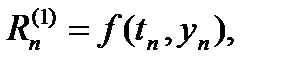
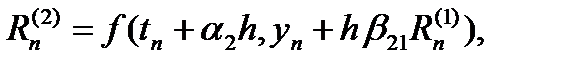
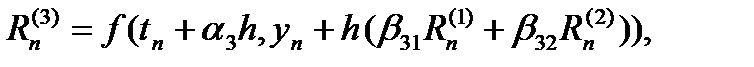
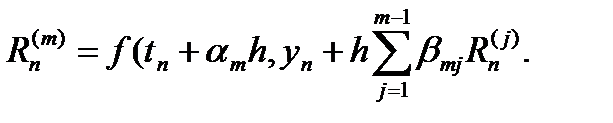
Выведенные формулы задают явный одношаговый метод вида

Где для вычисления функции 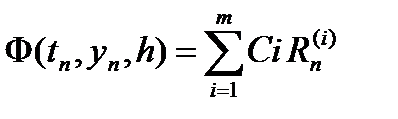используются значения правой части f в m вспомогательных точках. Поэтому этот метод называют явным m - этапным методом Рунге – Кутты.

Выбор конкретных значений параметров c_i, a_i, β_ij осуществляется, исходя из различных соображений. Естественно, что одним из основных является желание сделать порядок аппроксимации max возможным.

Устойчивость и сходимость

Следующая теорема позволяет в дальнейшем называть методы Рунге – Кутты, имеющие р-й порядок аппроксимации, методами р-го порядка точности.

Теорема 1. Пусть правая часть дифференциального уравнения удовлетворяет условию . Тогда всякий явный m - этапный метод Рунге-Кутты устойчив на конечном отрезке.

Следствие. Пусть выполнено условие 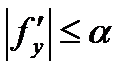. Тогда если явным m - этапный метод Рунге-Кутты имеет р-й порядок аппроксимации, то он сходиться с р-м порядком точности.

Семейство явных двухэтапных методов

Выведем расчетные формулы семейства явных двухэтапных методов Рунге-Кутты второго порядка точности. Запишем формулы явного двухэтапного метода

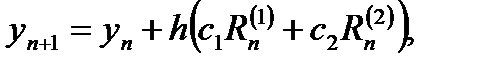
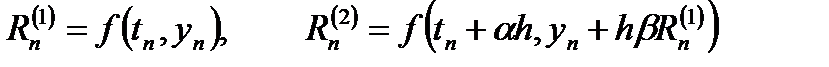
в виде

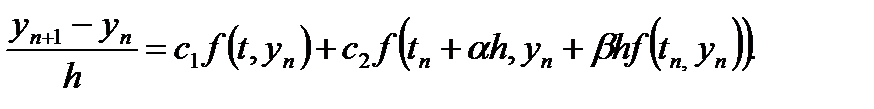
Параметрами этого метода является величины c₁, c₂, a, β. Представим погрешность аппроксимации

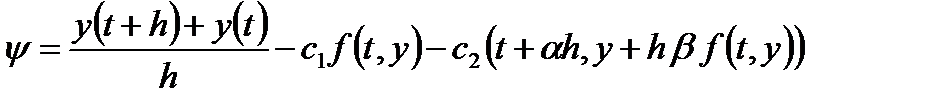
(где t=t_n, y=y(t_n), y(t_n) – решение дифференциального уравненияy¢(t,y)) в виде разложения по степеням h.

Формула Тейлора

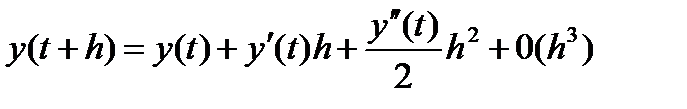
С учетом равенств (см. (10)) дает формулу

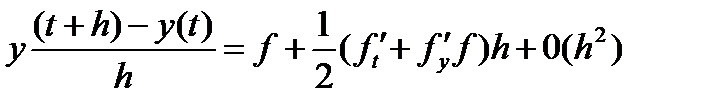
Дата добавления: 2018-06-27; просмотров: 538; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!