Использование формулы Тейлора

Численные методы решения задачи Коши

Для обыкновенных дифференциальных уравнений

На практике часто приходиться иметь дело с техническими системами и технологическими процессами, характеристики которых непрерывным образом меняются со временем t. Соответствующие явления, как правило, подчиняются физическим законам, которые формируются в виде дифференциальных уравнений. Одной из основных математических задач, которые приходиться решать для таких уравнений, является задача Коши (или начальная задача). Чаще всего к ней приходят тогда, когда начальное состояние некоторой физической системы в момент времени t₀ считается известным, и требуется предсказать её поведение при t ≥ t₀. Понимание того, что задача Коши описывает развитие тех или иных процессов во времени, значительно упрощает восприятие как подходов к её решению, так и оценки качества приближений.

Задачи Коши для дифференциального уравнения первого порядка.

Постановка задачи. Как известно, решением обыкновенного дифференциального уравнения первого порядка

y¢ (t) = f(t, y(t)) (1)

k = tga = f(t, y)

называется дифференцируемая функция y(t), которая при подстановке в уравнение (1) обращает его в тождество. График решения дифференциального уравнения называют интегральной кривой, а процесс нахождения решения дифференциального уравнения называют интегрирование этого уравнения.

(t, y)

Исходя из геометрического смысла производной y¢, заметим, что уравнение (1) задает в каждой точке (t, y) плоскости переменных t, y значение f(t, y) тангенса угла a наклона к оси 0t касательной к графику решения, проходящего через эту точку. Величину k = tga = f(t, y) будем называть угловым коэффициентом (рис.1).

Рис.2б

Рис.1

Если теперь в каждой точке (t, y) задать с помощью некоторого вектора направление касательной, определяемое значением f(t, y), то получиться так называемое поле направлений (рис.2а). Таким образом, геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной (рис.2б).

G AAgAAAAhAI5AU0nfAAAACQEAAA8AAAAAAAAAAAAAAAAArgwAAGRycy9kb3ducmV2LnhtbFBLBQYA AAAABAAEAPMAAAC6DQAAAAA= ">

Рис.2а

Начальное значение (t₀, y₀)

Для того, чтобы выделить из семейства решений дифференциального уравнения (1) одно конкретное решение, задают начальное условие

y(t₀) = y₀, (1)

где t₀ – некоторое фиксированное значение аргумента t, y₀ – величина, называемая начальным значением.

Геометрическая интерпретация использования начального условия состоит в выборе из семейства интегральных кривых той кривой, которая проходит через фиксированную точку (t₀, y₀).

Задачу нахождения при t>t₀решенияy(t) дифференциального уравнения (1), удовлетворяющего начальному условию (2), будем называть задачей Коши.

В некоторых случаях представляет интерес поведение решения при всех t>t₀. Однако чаще ограничиваются определением решения на конечном отрезке [t₀, T].

Численные методы решения задачи Коши. Основные понятия и определения.

2.1. Сетки и сеточные функции.

Первый этап на пути построения численного метода решения задачи Коши состоит в замене отрезка [t₀, T] – области непрерывного изменения аргумента t– множеством 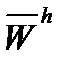, которое состоит из конечного числа точек t₀<t₁< … <t_N = T и называется сеткой. Сами точки t_i называются узлами сетки, а величина h_n = t_n - t_n_-1 – шагом сетки (рис. 3)

t₀

t₁

t_n-1

t_n

t_N= T

h_n

Рис. 3

. . . . . . . . . .

Для упрощения изложения будем рассматривать равномерные сетки, то есть такие сетки, у которых шаг h_n постоянен. В этом случае h_n = h = (T – t₀) / N и t_n = t₀ + nh, n = 1, 2, …, N.

Наряду с функциями непрерывного аргумента будем рассматривать и сеточные функции, то есть такие функции, которые определены лишь в узлах сетки 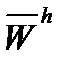. Для того, чтобы отличать сеточные функции от функций непрерывного аргумента, будем помечать их индексом h, например, u^h – сеточная функция. Для краткости записи значения u^h(t_n) сеточной функции u^h в узлах t_n сетки 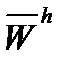будем обозначать через Un.

Следующий этап в построении численного метода состоит в замене задачи Коши её дискретным аналогом – системой уравнений, решая которую можно последовательно находить значения y₁, y₂, …, y_N сеточной функции y^h, играющие роль приближений к значениям решения задачи Коши в узлах сетки .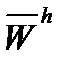

В основе построения конкретного численного метода лежит тот или иной способ замены дифференциального уравнения y¢ = f(t, y) его дискретным аналогом – уравнением вида

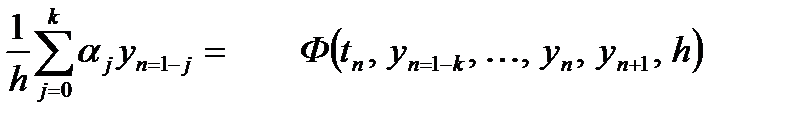(3)

в которое входят значения сеточной функции y^h в k+1 последовательных точках t_n_+1-_k, …, t_n, t_n₊₁

Предполагается, что a₀¹ 0.

Во всех рассматриваемых методах сумму

(4)

стоящую в левой части уравнения (3), можно рассматривать как разностную аппроксимацию производной y¢ в соответствии с одной из формул численного дифференцирования. Правую часть Ф уравнения (3) можно рассматривать как специальным образом построенную аппроксимацию функции f.

Значение y_n₊₁ приближенного решения в очередной точке находится из уравнения (3), при этом используются найденные ранее значения сеточной функции y^h в k предыдущих точках t_n_+1-_k, …, t_n. Поэтому такие методы получили название r – шаговых. Как нетрудно видеть, для того, чтобы найти значения сеточной функции y^h во всех узлах сетки 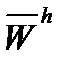, используя k– шаговый метод, необходимо задать r начальных значений

y^h (t₀) = y₀, y^h (t₁) = y₁, …, y^h (t_k_-1) = y_k_-1 (5)

Задачу вычисления сеточной функции y^h, удовлетворяющей уравнению (3) для всех n ≥ r - 1 и принимающей заданные начальные значения (5), будем называть дискретной задачей Коши.

При уравнение (3) упрощается и принимает вид

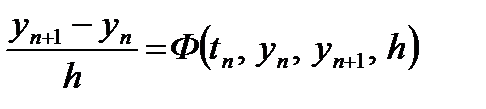(6)

Соответствующий метод принято называть одношаговым. Вычисление значения y_n₊₁ осуществляется здесь с использованием только одного предыдущего значения y_n. Поэтому одношаговые методы часто называют самостартующими.

Простейший дискретный аналог дифференциального уравнения (1) представляет собой уравнение

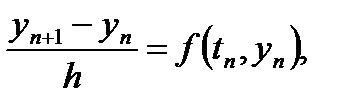(7)

приводящее к методу Эйлера.

/* Леонард Эйлер (1707 - 1783) – математик, физик, механик, астроном. Родился в Швейцарии, с 1726 по 1741 и с 1776 по 1783 работал в России*/

При r> 1 численный метод называется многошаговым.

Использование формулы Тейлора

Один из наиболее простых для понимания подходов к решению задачи Коши основан на использовании формулы Тейлора.

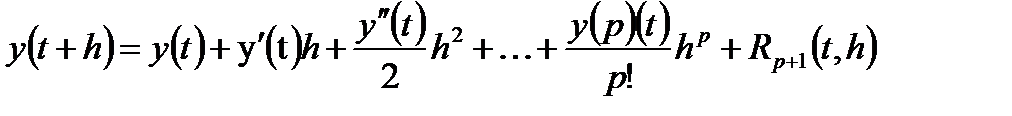(8)

Где - остаточный член формулы Тейлора, ξ – некоторая точка, принадлежащая отрезку [t, t+h].

Если значение решения y в ()t известно, то в силу равенства

y¢(t) = f(t, y(t)) (9)

значение производной y¢(t) также можно считать известным.

Для того, чтобы вычислить производные 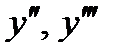, … более высокого порядка, входящие в формулу (8), продифференцируем равенство (9) по t, использовав правило дифференцирования сложной функции. Тогда получим

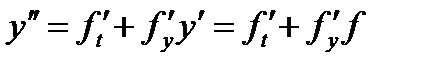(10)

и т.д. (11)

Нетрудно заметить, что выражения для производных y⁽^k⁾ усложняются по мере роста порядка k.

Использование приближенной формулы (8) приводит к явному одношаговому методу:

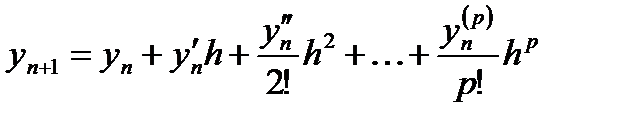(12)

Здесь 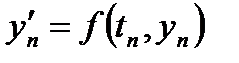, значения и 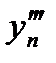получаются в результате подстановки в формулы (10), (11) значений t = t_n и y = y_n, аналогично вычисляются значения при k> 3.

Локальная погрешность этого метода l_n совпадает с величиной R_p₊₁ (t_n, h) остаточного члена формулы Тейлора, пропорциональной h^p⁺¹. Нетрудно доказать, что метод (12) сходится и имеет порядок точности, равный .

Несмотря на то, что рассматриваемый метод теоретически дает возможность найти решение с любым порядком точности, на практике он применяется довольно редко. Дело в том, что использование формулы (12) приводит к необходимости вычисления большого числа производных, что чаще всего является весьма трудоемкой и нередко аналитически невыполнимой операцией.

Более существенный аргумент против использования метода (12) состоит в том, что в настоящее время разработаны эффективные численные методы решения задачи Коши, предполагающие необходимость вычисления значения только функции f и не использующие её частные производные.

Тем не менее, для решения некоторых специальных классов задач приведенный выше метод может быть полезен. В частности, он используется при решении некоторых задач небесной механики, в которых вычисление производных y⁽^k⁾ не требует существенных дополнительных затрат в силу специальной структуры правых частей.

Метод Эйлера

Метод Эйлера является простейшим и исторически первым численным методом решения задачи Коши. Его можно получить, если в приближенном равенстве (12) оставить только два первых слагаемых, то есть взять p=1. Тогда формула (12) примет вид:

y_n+1 = y_n + hf (t_n, y_n) (13)

tga_n= k_n= f(t_n, y_n)

a_n

t_n

t_n+1

y_n

y_n+1

l_n

Рис.4

Геометрическая интерпретация одного шага метода Эйлера заключается в аппроксимации решения на отрезке [t_n, t_n₊₁] касательной y = y_n + y¢ (t_n) (t - t_n), проведенной в (×) (t_n, y_n) к интегральной кривой, проходящей через эту точку (рис.4).

/m De8jW062VQP1vnFsIJ5FoIgLVzZcGfjevT88g/IBucTWMRm4kodlfnuTYVq6kb9o2IZKiQj7FA3U IXSp1r6oyaKfuY5YuJPrLQZZ+0qXPY4ibls9j6InbbFhcaixo3VNxXl7sQY+RhxXj/HbsDmf1tfD bvG538RkzP3dtHoFFWgKf8/wG1+iQy6Zju7CpVetASkS5JokAoRezF8SUEcBMqDzTP8vkP8AAAD/ /wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50 X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAA X3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAUZaHSsQLAAAngwAADgAAAAAAAAAAAAAAAAAuAgAA ZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEA9CH11twAAAAIAQAADwAAAAAAAAAAAAAAAAAe DgAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAACcPAAAAAA== ">

t₀

t₂

t₁

t₃

y₀

y₁

y₂

y₃

a₁

a₂

a₃

a₄

Рис.5

Таким образом, после выполнения N шагов неизвестная интегральная кривая заменяется ломаной линией (ломаной Эйлера), для которой угловой коэффициент k_n очередного производного звена равен значению f(t_n, y_n) (рис.5).

Итак, метод Эйлера является явным одношаговым методом, для него погрешность аппроксимации имеет вид: 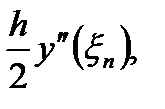так как метод Эйлера устойчив на конечном отрезке и имеет первый порядок аппроксимации. Оценивая метод Эйлера, необходимо учитывать, что при его реализации на ЭВМ неизбежно возникнут погрешности округления. В результате фактически вычисляемые значения 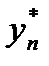будут удовлетворять соотношению Величины δ_n учитывают вклад погрешностей округления. Для определения численных значений величин δ_nрассмотрим теорему.

Теорема. Пусть функция f удовлетворяет условию Тогда для метода Эйлера справедлива такая оценка глобальной погрешности

maxïy (t_n) - y_nï£C (T) h, (14)

0 £ n £N

гдеC (T) = ℮^{L (T - to)}(T - to) M₂ / 2,

M₂ = max /y¢¢ (t)/

[to, T]

Доказательство: ┘Ψn – погрешностьаппроксимации, тогдаy(tn + 1) = y(tn) + h(f (tn, y(tn) + Ψn).Пологая, что заметим, что сеточная функция 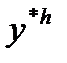является решением дискретной задачи Коши, где . В силу устойчивости метода Эйлера (которую мы приняли без доказательства) справедлива оценка

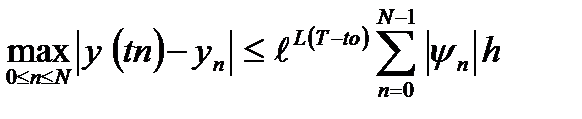
Учитывая, что 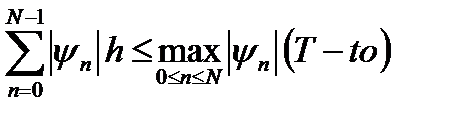и используя то обстоятельство, что метод Эйлера имеет первый порядок аппроксимации, то есть

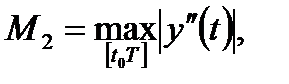
получим неравенство (14), ч.т.д.

Используя последнюю теорему, мы можем записать следующую оценку погрешностей округления

(15)

где δ – некоторое среднее значение величины ïδnï, аN=(T – t₀) / h

Таким образом, с учетом неравенств (14), (15) получается следующая оценка погрешности фактически вычисляемых значений y_n*:

honm

Emin

Рис.6

Схематически график функции приведен на рис. 6, из которого очевидно, что полная погрешность убывает только лишь при уменьшении шага h до некоторого значения honm. Достижимая точность метода ограничена снизу значением Emin, и попытка увеличить точность за счет уменьшения шага h при h<honm . приводит к резкому росту погрешность.

Значение honm, как правило, бывает очень трудно определить заранее. Однако, если очень высокая точность не нужна, то необходимый для её достижения шаг обычно бывает много больше honm.

Если же требуется высокая точность решения, то достигнуть её с помощью метода Эйлера нельзя, даже если пойти на значительные затраты машинного времени, неизбежные при расчете с малым значением шага h.

/* Необходимо иметь в своем распоряжении методы, имеющие более высокий порядок точности и позволяющие вести расчет со сравнительно крупным шагом h. */

Дата добавления: 2018-06-27; просмотров: 308; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!