Задачи с параметром, решаемые с помощью аналитического метода
Пример. Найти все значения параметра  , для каждого из которых больший корень уравнения
, для каждого из которых больший корень уравнения 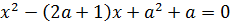 в пять раз больше, чем его меньший корень.
в пять раз больше, чем его меньший корень.
Решение. Рассмотрим данное уравнение как квадратное с переменной x. Из условия задачи следует, что это уравнение должно иметь два различных корня, что возможно в том и только в том случае, если дискриминант D уравнения положителен. Тогда:
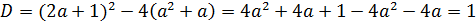
Пусть  и
и  – соответственно меньший и больший корни уравнения.
– соответственно меньший и больший корни уравнения.
Поскольку 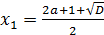 и
и 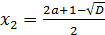 ,
,
то 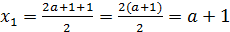 и
и 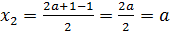 .
.
По условию 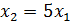 , отсюда следует,
, отсюда следует,
что 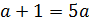
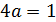
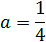
Ответ: 
Пример. Найти все значения параметра  , при каждом из которых неравенство
, при каждом из которых неравенство 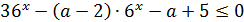 имеет единственный корень.
имеет единственный корень.
Решение. Сделаем замену переменной. Пусть 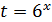 . Неравенство примет вид
. Неравенство примет вид 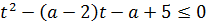 . Поскольку
. Поскольку 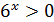 при любом действительном значении переменной, задачу можно переформулировать так: найти все значения параметра
при любом действительном значении переменной, задачу можно переформулировать так: найти все значения параметра  , при каждом из которых неравенство
, при каждом из которых неравенство 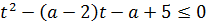 имеет единственный положительный корень. Если это неравенство имеет корни
имеет единственный положительный корень. Если это неравенство имеет корни 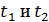 , то их сумма равна
, то их сумма равна 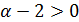 , поскольку
, поскольку 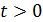 .
.

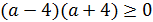
(здесь график), откуда 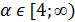 .
.
Ответ: 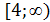 .
.
Пример. Найти наибольшее и наименьшее значения выражения
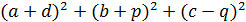 , если числа a, b, c, d, p, q таковы, что
, если числа a, b, c, d, p, q таковы, что
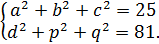
Решение. Выражение 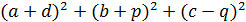 есть квадрат расстояния между точками (a;b;c) и (-d; -p; q). Первая точка лежит на сфере с центром в начале координат и
есть квадрат расстояния между точками (a;b;c) и (-d; -p; q). Первая точка лежит на сфере с центром в начале координат и 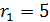 , а вторая точка лежит на сфере с тем же центром и
, а вторая точка лежит на сфере с тем же центром и 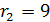 .
.
Наибольшее расстояние: 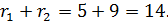
Наименьшее расстояние: 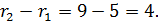
Отсюда следует, что искомые значения равны 196 и 16.
|
|
|
Ответ: 196; 16.
Пример. Найдите все значения параметра  , для каждого из которых уравнение
, для каждого из которых уравнение 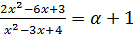 имеет хотя бы один корень.
имеет хотя бы один корень.
Решение. Заметим, что левая часть уравнения определена при любом действительном значении переменной, поскольку дискриминант квадратного трёхчлена в знаменателе дроби отрицателен и, следовательно, не обращается в нуль. Рассмотрим данное уравнение как уравнение второй степени с переменной x, приведя его к стандартному виду. Выполним необходимые преобразования:
( 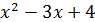 ) (
) ( 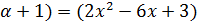
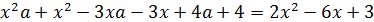
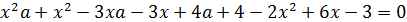
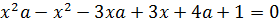
( 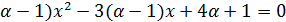
При  уравнение принимает вид 0
уравнение принимает вид 0  и не имеет корней.
и не имеет корней.
При  уравнение является квадратным и имеет хотя бы один корень в том и только в том случае, если его дискриминант D неотрицателен (или, что тоже, если
уравнение является квадратным и имеет хотя бы один корень в том и только в том случае, если его дискриминант D неотрицателен (или, что тоже, если 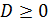 ). Поскольку
). Поскольку
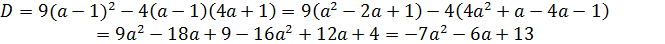
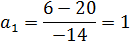
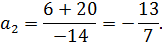
Тогда  , получаем неравенство
, получаем неравенство
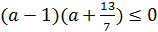 , из которого с учётом условия
, из которого с учётом условия  находим, что
находим, что 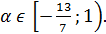
Ответ:  .
.
Пример.Найти наименьшее значение параметра  , для которого существует хотя бы одна пара
, для которого существует хотя бы одна пара  таких чисел
таких чисел 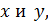 что
что 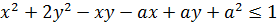 .
.
Решение.Рассмотрим данное неравенство как квадратное с переменной  , переписав его в виде:
, переписав его в виде:
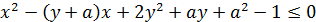 .
.
Так как коэффициент при второй степени переменной положителен, то квадратный трехчлен в левой части неравенства может принимать неположительные значения тогда, когда 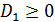 .
.
|
|
|
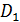 =
= 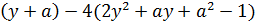
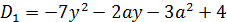 .
.
Рассмотрим 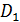 как квадратный трехчлен относительно
как квадратный трехчлен относительно  . Так как коэффициент при второй степени этого трехчлена отрицателен, принимать неотрицательные значения он может в том случае, если
. Так как коэффициент при второй степени этого трехчлена отрицателен, принимать неотрицательные значения он может в том случае, если 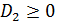
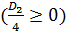
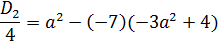
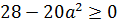
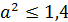
 .
.
Значит, 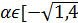 ;
; 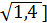 , и наименьшим возможным значением параметра
, и наименьшим возможным значением параметра  является
является  .
.
Ответ.  .
.
Пример. При каких значениях параметра  уравнение
уравнение

Имеет ровно три различных корня? Найдите все возможные значения  .
.
Решение. Для начала составим систему:

Возведём правую часть уравнения нашей системы в квадрат:
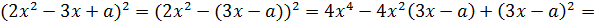

Тогда уравнение системы примет вид:
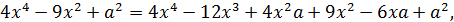
Поэтому преобразуем данное уравнение:
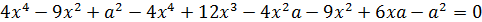
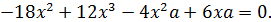
Сделаем группировку слагаемых:
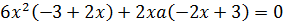
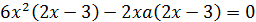
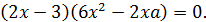
Следовательно, получим два уравнения: 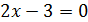 и
и 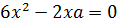 .
.
Решением первого уравнения является:
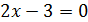
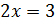
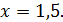
Решением второго уравнения является;
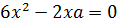
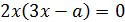
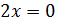 и
и 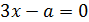
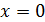 и
и 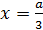 .
.
По условию задачи нам требуется три различных корня уравнения, поэтому, чтобы они не совпали, исключим:
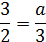
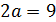
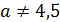
и
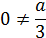

Теперь найдём при каких  эти три корня будут решением неравенства нашей системы:
эти три корня будут решением неравенства нашей системы:
При 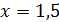
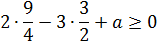
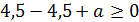
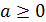
При 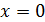
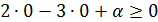
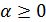
При 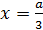
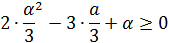
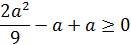
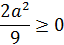
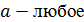
Ответ: 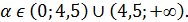
Пример. Найти все значение параметра  , при котором уравнение
, при котором уравнение
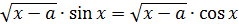
имеет один корень на отрезке 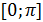 .
.
Решение. Сначала решаем данное уравнение:
|
|
|
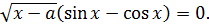
Отсюда получаем два уравнения:  и
и 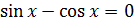 .
.
Из первого уравнения следует, что 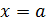 .
.
Теперь решим второе уравнение:
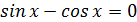
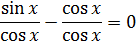
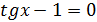


Теперь составим систему условий, которые обязательно должны выполняться:
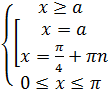
Получаем:
Если 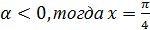 – единственный корень;
– единственный корень; 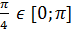 .
.
Если 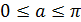 , то
, то 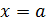 является решением, но тогда на промежутке
является решением, но тогда на промежутке 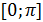 будет два корня:
будет два корня: 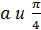 .
.
В результате получаем, что 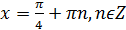 является решением, когда:
является решением, когда:
1) 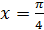
2) 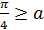
3) 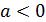 .
.
Следовательно, если 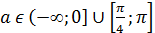 , то данное уравнение будет иметь одно решение на отрезке [0;
, то данное уравнение будет иметь одно решение на отрезке [0; 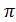 ].
].
Ответ: 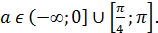
Пример. Найдите все значения параметра  , при которых уравнение
, при которых уравнение
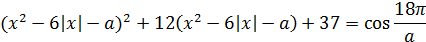
имеет ровно два корня.
Решение. Пусть 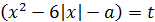 , тогда уравнение примет вид:
, тогда уравнение примет вид:
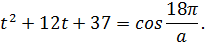
Выделим полный квадрат в левой части уравнения:
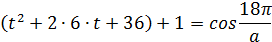
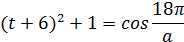
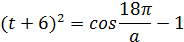
Составим систему: 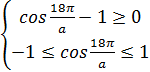
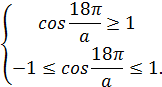
Следовательно, 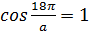 ,
,
тогда 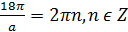
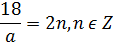
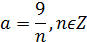
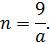
Так как 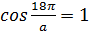 , тогда
, тогда
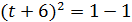
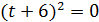

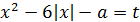 , тогда
, тогда
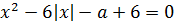
Сделаем замену: 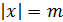
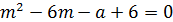
Если у нас получится два положительных корня, то всего у нас будет четыре корня, следовательно, мы не рассматриваем этот вариант. Тогда:
1) 
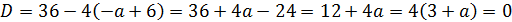
Тогда получаем, что 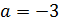 .
.
Если 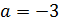 , то
, то 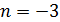 .
.
2) 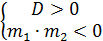
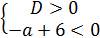
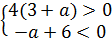
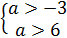
Тогда получаем, что 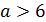 .
.
Если 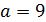 , то
, то 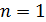 .
.
Ответ: 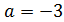 ,
, 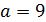 .
.
Пример. Найдите все значения  , при которых система
, при которых система
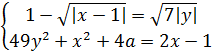
имеет ровно четыре различных решения.
Решение. Рассмотрим второе уравнения данной системы:
|
|
|
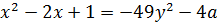
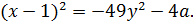
Тогда система примет вид:

Сделаем замену:
 и
и 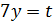 .
.
Получим, что:
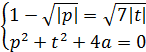
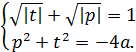
Так как перестановка переменных в уравнении данной системы не влияет на решение этой системы, то если корнем является
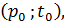
то и  ,
, 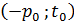 ,
, 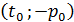 ,
, 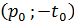 ,
, 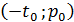 ,
, 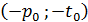 ,
, 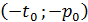 тоже являются корнями.
тоже являются корнями.
Необходимым условием для существования системы с четырьмя решениями является:
1) 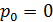 , тогда эти восемь корней попарно совпадут, в результате чего мы получим четыре корня, а именно:
, тогда эти восемь корней попарно совпадут, в результате чего мы получим четыре корня, а именно: 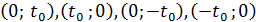 ,
,
тогда
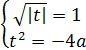
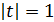
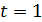 и
и 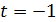 .
.
Если 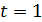 , то
, то 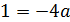 , откуда
, откуда  .
.
Если 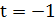 , то
, то 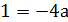 , откуда
, откуда 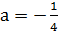 .
.
Отсюда 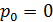 – необходимое условие для существования четырёх решений.
– необходимое условие для существования четырёх решений.
Значит, найдя нужные  , сделаем проверку, подставив в систему корень (0; 1) и
, сделаем проверку, подставив в систему корень (0; 1) и  :
:
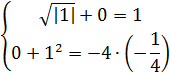
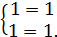
Также, если мы подставим другие корни (0; -1), (-1; 0), (1; 0), то увидим, что  .
.
2) 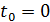 , тогда эти восемь корней попарно совпадут, в результате чего мы получим четыре корня, а именно:
, тогда эти восемь корней попарно совпадут, в результате чего мы получим четыре корня, а именно: 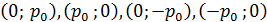 ,
,
тогда
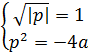
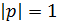
 и
и 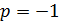 .
.
Если  , то
, то 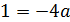 , откуда
, откуда  .
.
Если  , то
, то 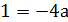 , откуда
, откуда 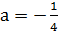 .
.
Отсюда 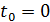 – необходимое условие для существования четырёх решений.
– необходимое условие для существования четырёх решений.
Значит, найдя нужные  , сделаем проверку, подставив в систему корень (0; 1) и
, сделаем проверку, подставив в систему корень (0; 1) и  :
:
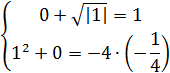
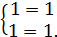
Также, если мы подставим другие корни (0; -1), (1; 0), (-1; 0), то увидим, что  .
.
3) 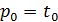
Пусть 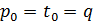 , тогда эти восемь корней попарно совпадут, в результате чего мы получим четыре корня, а именно: (q; q), (-q; q), (q; -q), (-q; -q).
, тогда эти восемь корней попарно совпадут, в результате чего мы получим четыре корня, а именно: (q; q), (-q; q), (q; -q), (-q; -q).
Тогда
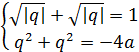
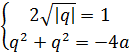


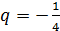 и
и 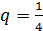 .
.
Если 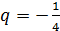 , то
, то  ,
, 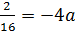 ,
, 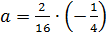 ,
, 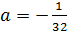 .
.
Если 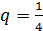 , то
, то  ,
, 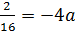 ,
, 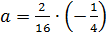 ,
, 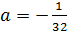 .
.
Отсюда 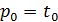 – необходимое условие для существования четырёх решений.
– необходимое условие для существования четырёх решений.
Значит, найдя нужные  , cделаем проверку, подставив в систему корень (q; q) и
, cделаем проверку, подставив в систему корень (q; q) и 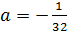 .
.
Также, если мы подставим другие корни (-q; q), (q; -q), (-q; -q), то увидим, что 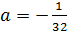 .
.
Ответ: 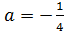 ,
, 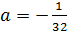 .
.
Пример. Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение
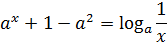
имеет решение, причем любой его корень находится в промежутке [1; 2].
Решение.Рассмотрим правую часть данного уравнения как 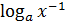 , а затем вынесем минус перед знаком логарифма:
, а затем вынесем минус перед знаком логарифма:
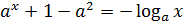

1) При 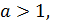 график
график 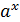 возрастает, график
возрастает, график 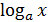 возрастает.
возрастает.
График 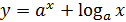 возрастает.
возрастает.
График 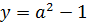 – постоянная функция и, следовательно, исходное уравнение имеет единственное решение. Значит, это решение должно находиться в промежутке
– постоянная функция и, следовательно, исходное уравнение имеет единственное решение. Значит, это решение должно находиться в промежутке 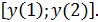
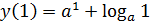 =
= 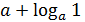 =
= 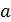
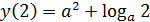
Составим систему:
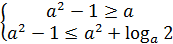
а) 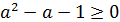
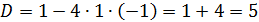
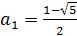 и
и 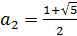
б) 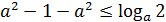
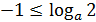
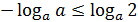
 , так как
, так как 
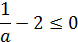
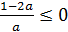 , так как
, так как 
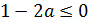
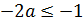
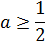
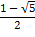
|
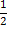
|
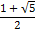
|
рис.2
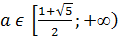 .
.
2) При 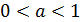
График 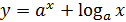 убывает.
убывает.
График 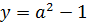 – постоянная функция и, следовательно, исходное уравнение имеет единственное решение. Значит, это решение должно находиться в промежутке
– постоянная функция и, следовательно, исходное уравнение имеет единственное решение. Значит, это решение должно находиться в промежутке 
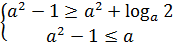
а) 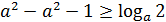
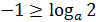
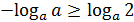
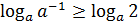 , так как
, так как 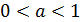
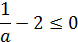
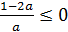 , так как
, так как 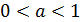
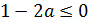
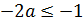
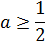
б) 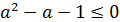
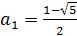 и
и 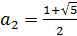
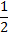
|
| 0 |
| 1 |
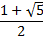
|
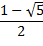
|
рис.3
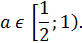
Ответ: 
Дата добавления: 2018-06-27; просмотров: 1151; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
