Основные свойства первообразной
1. Если F(x) первообразная для f(x), то при любой постоянной С функция F(x) + C также является первообразной для f(x) (таким образом: для F '(x) первообразной является функция F(x) + C);
2. Любые две первообразные F1(x) и F2(x) для одной и той же функции f(x)
отличаются на постоянную: F1(x) – F2(x) = С
Неопределенный интеграл: неопределенным интегралом от функции f(x) называется общее выражение F(x) + C, т.е. множество всех первообразных функции f(x). Здесь F(x) - какая-либо конкретная первообразная, С – произвольная постоянная. Неопределенный интеграл обозначается символом ∫f(x)dx (читается: "интеграл от функции f(x) дэ икс"). f(x) называется подынтегральной функцией, х - переменной интегрирования.
Таким образом, х2/2+C является неопределенным интегралом от функции у=х.
Свойства неопределенного интеграла
1. ∫ (f(x) + g(x))dx = ∫f(x)dx + ∫g(x)dx - интеграл от суммы функций
равен сумме интегралов от этих функций;
2. ∫C*f(x)dx = C ∫f(x)dx - постоянный множитель можно выносить за знак интеграла.

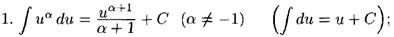
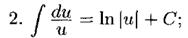
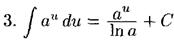
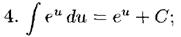
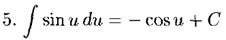
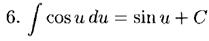
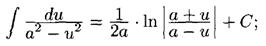
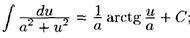
Таблицу можно использовать в двух вариантах: (1) u - простая переменная и (2) u - функция u(x), а du=u'(x)dx. Случай (2) реализует интегрирование с заменой переменной:
.
(1) Таблица верна, если u является простой переменной (аргументом функции).
Т.е. выражение ∫sin(u)du равносильно ∫sin(х)dх.
(2) Приведенная таблица также верна, если u является функцией от х (u(x)), т.е. подинтегральная функция является составной (функцией от функции).
При этом du - дифференциал функции: du=u'(x)dx.
Примеры.
1) Пусть u(х) = 3х+1. Тогда u'(x)=3, du(x)=3dx --> ∫[1/(3x+1)]3dx =∫1/(3x+1)du(x) =∫(1/u)du = ln|u| + C = ln|3x+1|+C Здесь значок "-->" обозначает " Следовательно".
или: ∫1/(3x+1)dx =(1/3) ∫[1/(3x+1)]3dx = (1/3) ln|3x+1|+C
2) Пусть u=sin(x). Тогда u'(x)=cos(x), du(x)=cos(x)dx
--> ∫sin(sin(x))cos(x)dx = ∫sin(u)u'(x)dx =∫sin(u)du= - cos(u)+C = - cos(sin(x))+ C
Простой алгоритм интегрирования составной функции для частного случая, когда u(x)=a*x+b - линейная функция.
Если ∫f(x)dx = F(x)+C, (т.е. F'(x) = f(x))
то: ∫f(ax+b)dx =(1/a)F(ax+b) + C
Примеры: 1) òе2C+1dx = (1/2)е 2C+1+C
- Заменяем е2х+1 на ех, òеCdx = ex+C. Затем выражение ex+C делим на 2 и заменяем в нем х на 2х+1.
2) ò1/(1+3х)dx = (1/3)ln|3х+1| + C - в 1/(1+3х) заменяем 1+3х на х,
ò1/хdx = ln|х|+C. Затем выражение ln|х|+C делим на 3 и заменяем в нем х на 3х+1.
3) ò(5х+1)3dx = (1/5)(1/4)(5х+1)4 + C
4) ∫sin(4x)dx= -1/4cos(3x) + C
Интегрирование по частям
(При решении дифференциального уравнения нередко бывает необходимым)
Пусть даны две функции u(x) и v(x), имеющие непрерывные производные.
Тогда: ∫u(x)v'(x)dx = u(x)v(x) -∫u'(x)v(x)dx, (4)
где v(x) - любая первообразная для заданной в правой части функции v'(x), т.е., если v'=x, то в качестве функции v можно использовать как х2/2, так и х2/2+5.
Пример: 1) ∫x*cos(x)dx= x*sin(x) - ∫ (x')*sin(x)dx = x*sin(x) - ∫sin(x)dx
2) ∫x*exdx= x*ex - ∫ (x')*exdx = x*ex - ∫exdx
Формула применяется в тех случаях, когда интеграл от функции u'(x)v(x) проще, чем от u(x)v'(x).
Данную формулу часто записывают в виде: ∫udv = uv - ∫vdu, где du=u'dx - дифференциал функции u(x).
* * *
Понятие комплексного числа
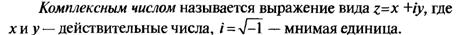

Тригонометрическая форма представления комплексного числа

Показательная форма представления комплексного числа
Можно показать: 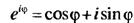
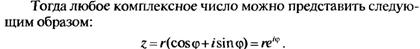
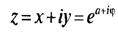 где a=ln(r)
где a=ln(r)
Примеры 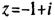
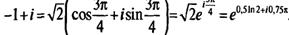

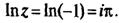
Дата добавления: 2018-06-01; просмотров: 315; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
